Exercices

66) Quels sont, parmi les énoncés ci-dessous, ceux qui sont vrais ?

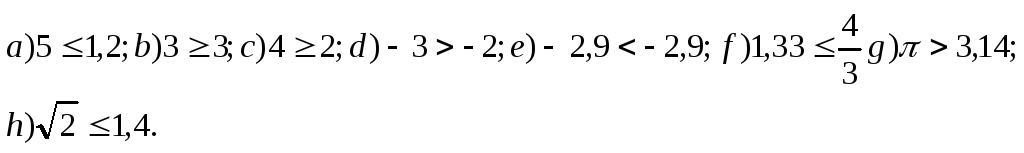
67) Quels sont les nombres entiers relatifs n tels que :

68) Recopier et compléter le tableau suivant :

départ	action	arrivée
	On multiplie chaque membre par 5.	5a ...
	...	b – 5 ...
	...	x ...
	...	y ...

69) Soit a un nombre tel que Compléter, si possible, par

70) Soit a un nombre tel que Compléter, si possible, par

71) Dans chacun des cas suivants, déterminer tous les entiers positifs n tels que :

72) Soit s et t tels que Compléter, si possible, par

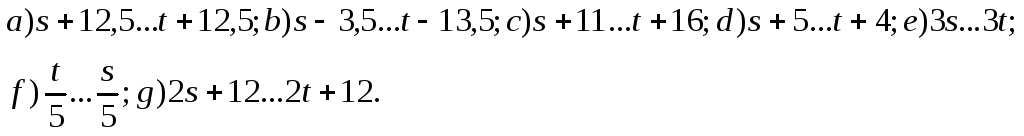
73) Soit b un nombre tel que Quelle inégalité peut-on déduire pour :

74) Soit x est un nombre tel que Quelle inégalité peut-on déduire pour :

75) Sans calcul, comparer les nombres suivants :

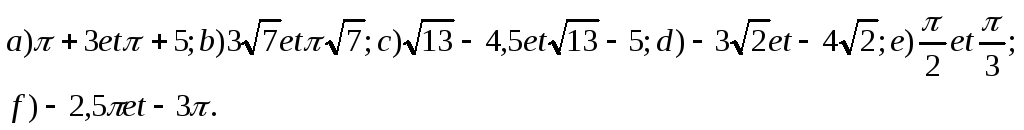
76) Un nombre a est tel que Compléter les inégalités :

77) Un nombre b est tel que Donner un encadrement de : a) 2b ; b) -4b ; c) 2b-3.

78) e est un nombre tel que Donner un encadrement de : a) e-2 ; b) 3e; c) -2e + 5.

79) L’unité de longueur est le mètre. Un rectangle de largeur l, de longueur L est tel que : Donner un encadrement du périmètre de ce rectangle.

2.2 Resoudre une inéquation

Mots à retenir

une inéquation (неравенство)

un intervalle (интервал, промежуток) semi-ouvert (полуоткрытый)

inclus (включённый) le crochet fermant : [...

exclu (исключённый) le crochet ouvrant : ]...

hachurer (штриховать)

Définitions

1) Une inégalité où figure un nombre inconnu désigné par une lettre s’appelle une inéquation.

Par exemple :

2) Résoudre une inéquation d’inconnue x, c’est trouver toutes les valeurs de x pour lesquelles l’inégalité est vraie. Ces valeurs sont les solutions de l’ inéquation.

La solution d'une inéquation n'est donc pas un nombre, mais un ensemble de nombres, aussi appelé intervalle.

On peut présenter l’ensemble des solutions par une phrase ou par une représentation graphique. Sur une droite graduée, on hachure les nombres qui ne sont pas solutions de l'inéquation.

noms	notations	inéquations	représentations graphiques
un intervalle ouvert	]a ; b[	a < x < b	a b
un intervalle fermé	[a ; b]	a ≤ x ≤ b	a b
un intervalle semi-ouvert	[a ; b[	a ≤ x < b	a b
un intervalle semi-ouvert	]a ; b]	a < x ≤ b	a b
un intervalle infini	]a ; +∞[	x > a	a
un intervalle infini	[a ; +∞ [	x ≥ a	a
un intervalle infini	]– ∞ ; b[	x < b	b
un intervalle infini	]– ∞ ; b]	x ≤ b	b

Si a n’est pas solution donc le crochet n’est pas dirigé du côté des solutions.

Si a est solution donc le crochet est dirigé du côté des solutions.

Remarques

1) Certaines inéquations n’ont pas de solution. Par exemple, n’a pas de solution car quelle que soit la valeur de x, n’est pas supérieur à 1.

2) Pour certaines inéquations, tous les nombres sont solutions. Par exemple, tous nombres sont solutions de l’inéquation car quelle que soit la valeur de x, est supérieur à -2.

Règles

Les propriétés des inégalités permettent de justifier les règles suivantes.

Règle 1 : on ne change pas les solutions d’une inéquation en ajoutant (ou en retranchant) une même expression à ses deux membres.

Règle 2 : on ne change pas les solutions d’une inéquation en multipliant (ou en divisant) ses deux membres par un nombre strictement positif.

Règle 3 : on ne change pas les solutions d’une inéquation en multipliant (ou en divisant) ses deux membres par un nombre strictement négatif et en changant le sens de l’inéquation.

Par exemple : résoudre l’inéquation

Solution

1) On simplifie l’écriture de l’inéquation en développant et en réduisant ses deux membres.

2) On regroupe les termes en x dans un membre, les termes constants dans l’autre.

3) On divise les deux membres par -3 et on change le sens de l’inéquation car

-3 < 0.

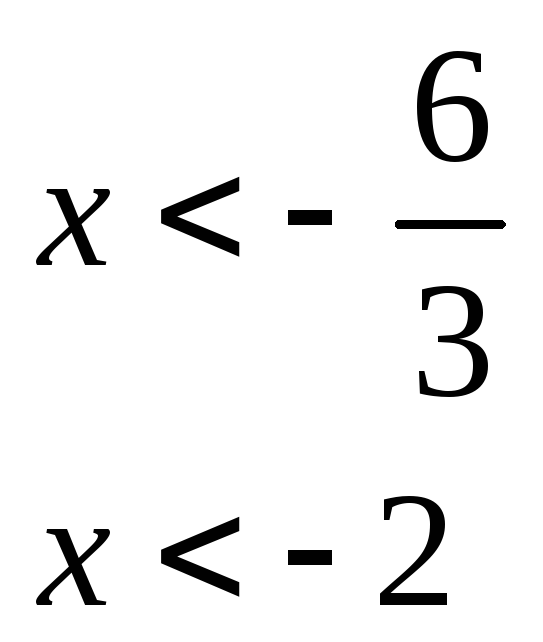
4) On représente les solutions sur une droite graduée en hachurant.

-2

Les solutions sont les nombres inrérieurs à -2.

Réponse : l’inéquation a pour solutions les nombres de l’intervalle ]– ∞ ; - 2[ .