
- •Sommaire
- •1. Activités géométriques
- •1. 1 Vocabulaire des vecteurs
- •1)La relation de Chasles
- •Exercices
- •1.2Vecteurs et coordonnées
- •Exercices
- •1.3 Propriété de Thalès
- •4) On donne la réponse sans oublier de rappeler l’unité de longueur.
- •3) On applique la réciproque de la propriété de Thalès pour conclure.
- •Exercices
- •1.4 Angles inscrits dans un cercle
- •Exercices
- •1.5 Révision
- •2. Inéquations à une inconnue
- •2.1Vocabulaire des inégalités
- •Exercices
- •2.2 Resoudre une inéquation
- •Exercices
- •2.3 Resoudre un système de deux inéquations
- •Exercices
- •2.4 Révision
- •3. Fonction trinôme du second degré
- •3.1 Trinôme du second degré
- •Exercices
- •3.2 Fonction trinôme du second degré
- •Exercices
- •3.3 Inéquations du second degré
- •Exercices
- •3.4 Révision
- •4. Suites
- •4.1 Notion de suite
- •Exercices
- •4.2 Suite arithmétique
- •Exercices
- •4.3 Suite géométrique
- •Exercices
- •4.4 Révision
1.5 Révision
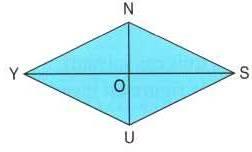
54) En utilisant la figure, où NSUY est un losange, écrire cinq égalités vectorielles.
55)Reproduire
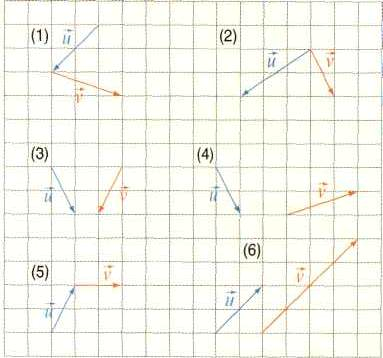
le dessin suivant sur papier quadrillé et, dans chacun des cas,
construire un représentant de la somme des vecteurs
![]()
56)Tracer
un quadrilatère ABCD. On appelle E le point tel que
![]() Quelle est la nature du quadrilatère ADEB ? Justifier.
Quelle est la nature du quadrilatère ADEB ? Justifier.
57) Dans le plan muni d’un repère, on considère les points : C (2,3 ; 3,4),
E (6,4 ;
1,2), R (-3,7 ; -2,8), F(-7,8 ; -0,6), M(-0,7 ; 0,3) .
Il est inutile de faire une figure. Calculer les coordonnées et les
normes des vecteurs![]() ,
,![]() ,
,![]() ,
,![]() .
.
Que constate-t-on ? Quelle est la nature du quadrilatère CERF ?
58) Dans le plan muni d’un repère, on considère les points suivants : A(1 ; 3),
B(0 ;
1), C(-2 ; -3). Calculer les coordonnées et les normes des
vecteurs
![]() et
et
![]() .
.
59) Soit
les points A(0 ; 1) et B(-3 ; 2) dans le repère. Quelles
sont les coordonnées du point C tel que
![]()
60) Dans un repère on donne les points : A(-1 ; 3) ; B(-4 ; 0) ; C(3 ; -1). Préciser la nature du triangle ABC.
61)
Dans un repère on donne les vecteurs![]() (2 ;
0),
(2 ;
0),
![]() (1 ;
2). et
(1 ;
2). et
![]() (-3 ;
m). Trouver m pour que les vecteurs
(-3 ;
m). Trouver m pour que les vecteurs
![]() et
et
![]() soient ortogonaux.
soient ortogonaux.
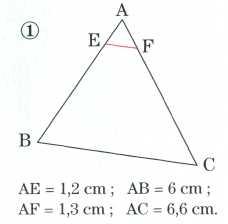
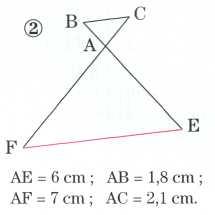
62) Dans chacun des cas, les points étant disposés comme sur les figures données, déterminer si les droites (EF) et (BC) sont parallèles.
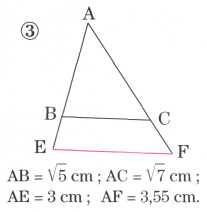
6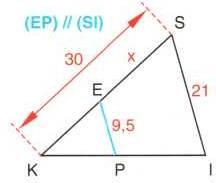
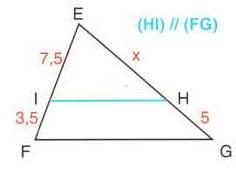 3)
Calculer x dans les cas suivants.
3)
Calculer x dans les cas suivants.
64) Compléter le texte qui accompagne la figure.
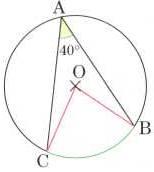
![]() est
... arc
est
... arc
![]() .
.
![]() est
... le même arc.
est
... le même arc.
Donc
![]() =
...= ... .
=
...= ... .
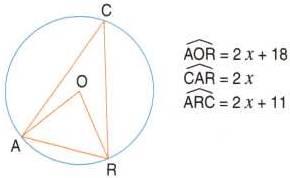
65)
Calculer
la mesuredes angles
![]() et
et
![]() sur
la figure suivante où O
sur
la figure suivante où O
est le centre du cercle.
2. Inéquations à une inconnue
2.1Vocabulaire des inégalités
Définitions
1)Les
expressions
![]()
![]()
![]() s’appellent
des inégalités.
s’appellent
des inégalités.
< se
lit « est strictement
inférieur
à ».
![]() se lit « est inférieur
ou égal
à ».
se lit « est inférieur
ou égal
à ».
> se lit
« est
strictement
supérieur
à ».
![]() se lit « est supérieur
ou égal
à ».
se lit « est supérieur
ou égal
à ».
Les doubles
inégalités :
![]() s’appellent
des encadrements
de
x.
s’appellent
des encadrements
de
x.
2) Pour comparer deux nombres relatifs, on peut calculer leur différence :
-
si
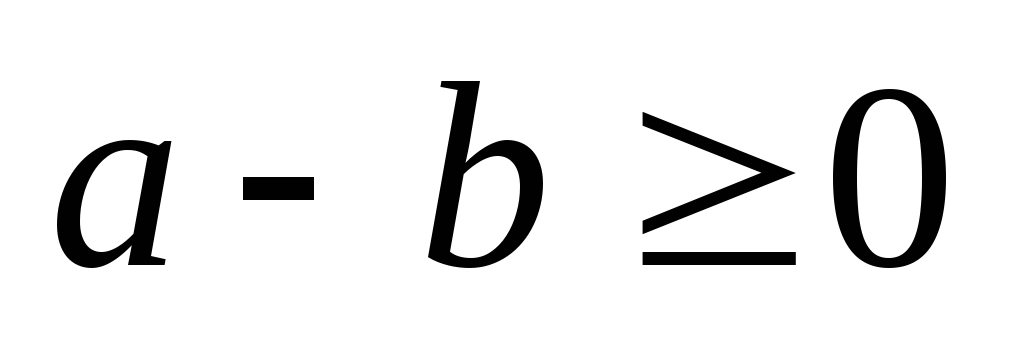 alors
alors
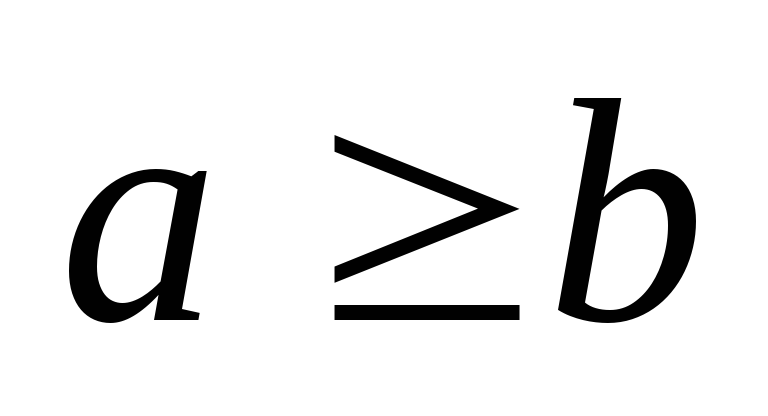 ;
; -
si
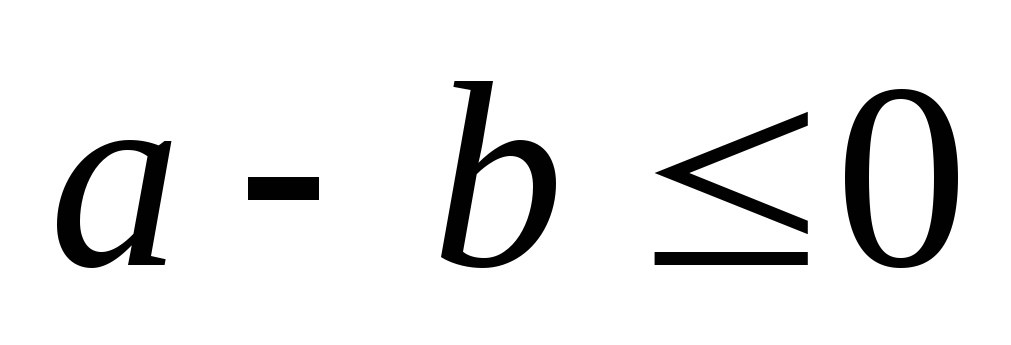 alors
alors
 .
.
Propriétés
1) Si on ajoute (ou on soustraire) un même nombre aux deux membres d’une inégalité, on ne change pas le sens de l’ inégalité.
Par exemple :
-
Si
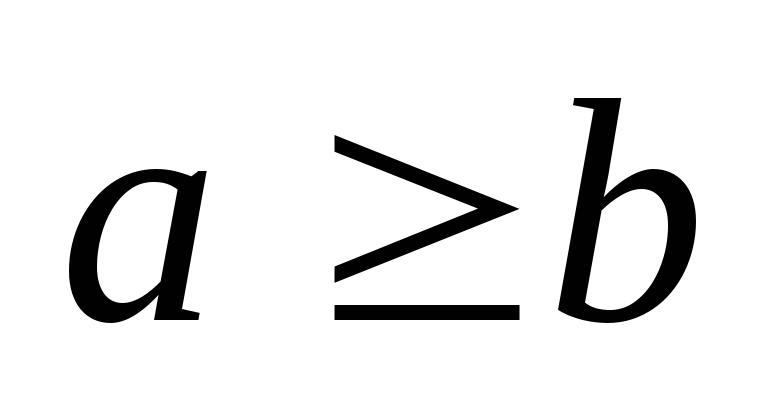 ,
alors
,
alors
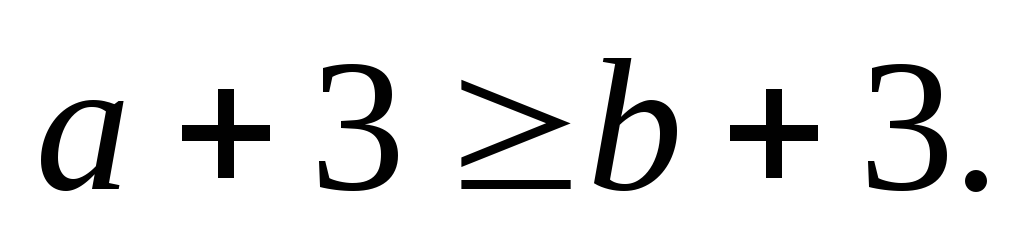
-
Si
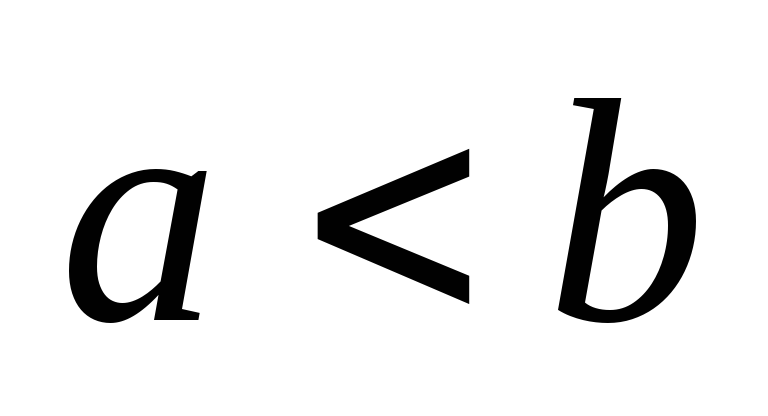 ,
alors
,
alors
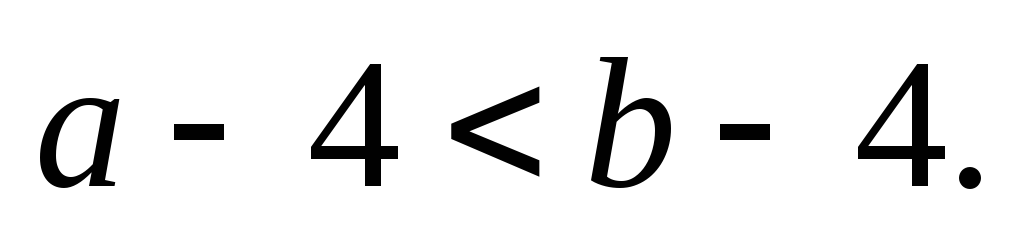
2) Si on multiplie (ou on divise) les deux membres d’une inégalité par un même nombre positif, on ne change pas le sens de l’ inégalité.
Par exemple :
-
Si
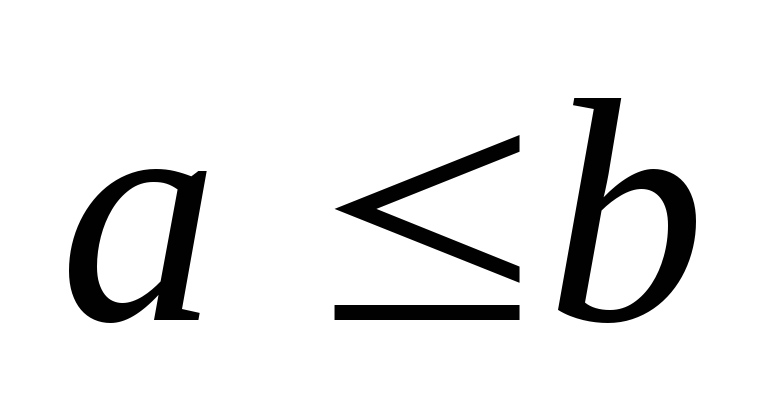 et
et
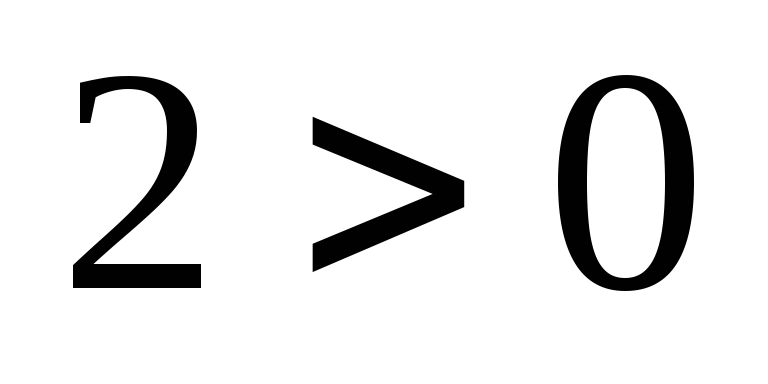 ,
alors
,
alors
 .
. -
Si
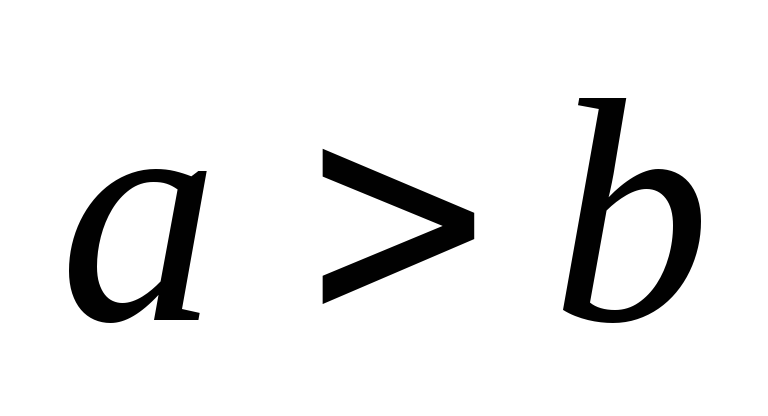 et
et
 ,
alors
,
alors
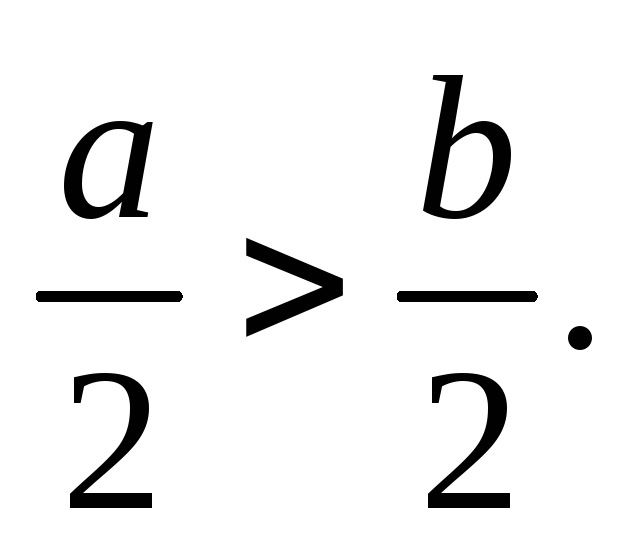
3) Si on multiplie (ou on divise) les deux membres d’une inégalité par un même nombre négatif, on change le sens de l’ inégalité.
Par exemple :
-
Si
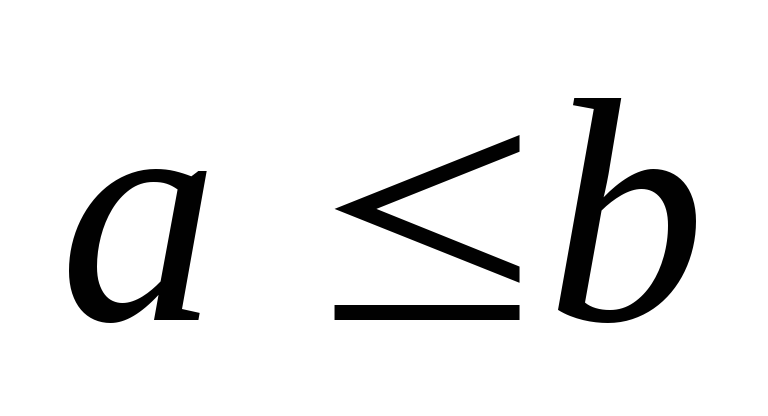 et
et
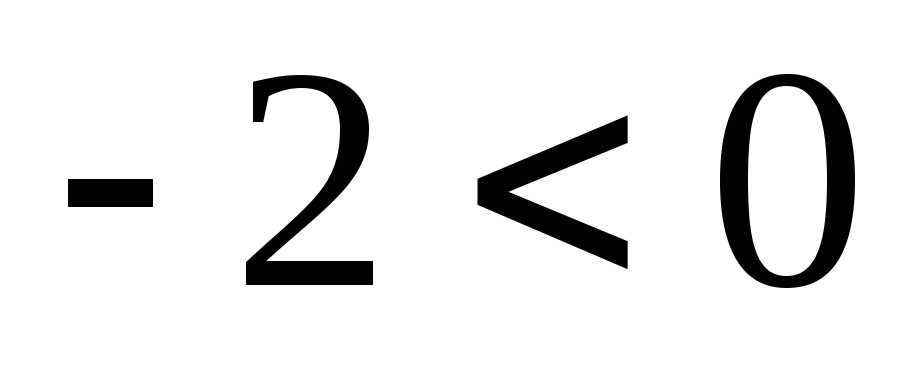 ,alors
,alors
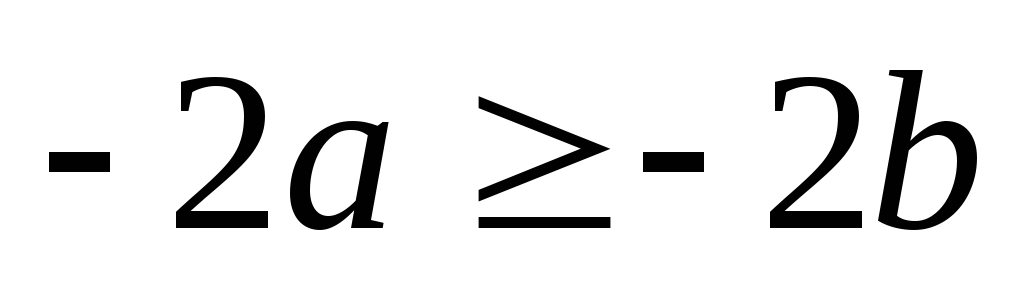 .
.
-
Si
 et
et
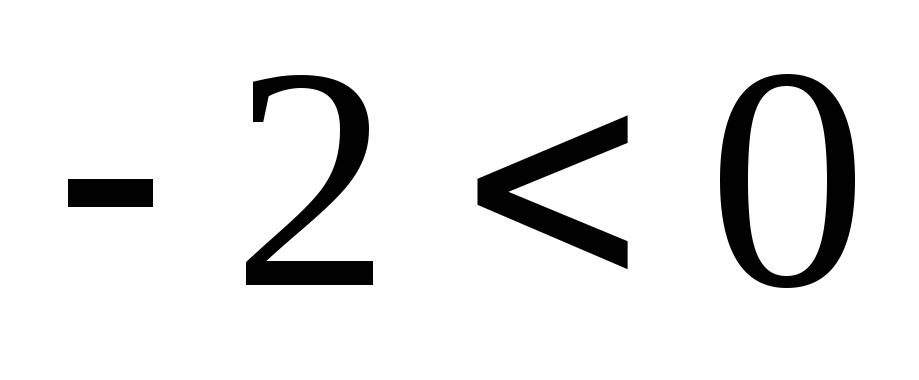 ,
alors
,
alors
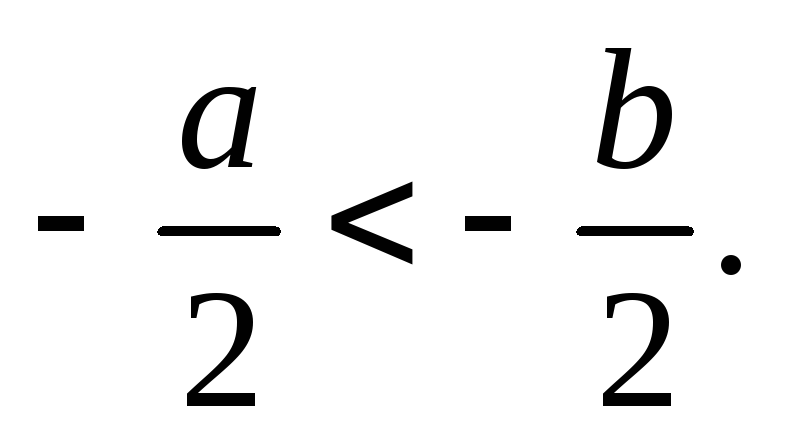
-2 est négatif, donc on a changé le sens de l’inégalité.
