Exercices

13) Lire les coordonnées des onze points marqués sur la figure. Lire les coordonnées des vecteurs,,,,et.

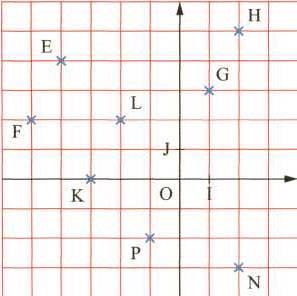
14) Lire les coordonnées des vecteurs de la figure ci-dessous.

15) Tracer un repère du plan et représenter les vecteurs (-4 ; 5), (2 ; 3) ;

(-5 ; 0) ; (0 ; 4).

16) Soit A(-2 ; 3), B(2 ; 4), C(5 ; -1), D(3 ; -2) ; E(-1 ; 5) et F(-4 ; -2). Calculer les coordonnées et les normes des vecteurs,,,.

17) Dans le plan muni d’un repère, on considère les points : A(-392 ; 183), B(22 ; -57), C(-187 ; -542), D(-601 ; -302). Il est inutile de faire une figure. Démontrer que les vecteurs et sont égaux. Que peut-on en déduire pour le quadrilatère ABCD ?

18) Dans un repère on donne les vecteurs (3 + 2x ; y + 1) et (5 + x ; 3y). Trouver x et y pour que les vecteurs et soient égaux.

19) Soit (4 ; 0) et (1 ;-2). Calculer les coordonnées des vecteurs et Calculer les normes des vecteurs.

20) Dans un repère on donne les vecteurs (6 ; -8) et (2 ;-3). Calculer les coordonnées des vecteurset Calculer les normes des vecteurs.

21) Soit les vecteurs . Déterminer une paire de vecteurs colinéaires entre eux.

22) Les vecteurs et sont-ils colinéaires ?

a) (5 ; -8) et (-3 ; 7). b) (4 ; -5) et (28 ; -35).

c) ( ; 3) et (6; ).

23) Dans un repère on donne les points A(-1 ; 0), B(-2 ; 2), C(2 ; -1) et D(0 ;m). Trouver m pour que les vecteurs et soient colinéaires.

24) Trouver le produit scalaire des vecteurset si

a) (1 ; -3) et (-4 ; -2). b)

c) d)

25) Dans un repère on donne les vecteurs(m ; -8) et (4 ; 3). Trouver m pour que les vecteurs soient ortogonaux.

26) Dans un repère on donne les points A(4 ; 5), B(-3 ; 3) et C(2 ; -2). Quelle est la nature du triangle ABC ?

27) Soit A(1 ; 4), B(-1 ; 8), C(9 ; 8) trois points du plan muni d’un repère. Démontrer que le triangle ABC est rectangle en A.

28) Dans le plan muni d’un repère on considère les points M(3 ; 5), E(-4 ; 6) et R(2 ; -2). Démontrer que le triangle MER est rectangle et isocèle.

29) Dans le plan muni d’un repère, on considère les points A(9 ; -4), B(4 ; -3), C(1 ; 1), D(6 ; 0). Démontrer que les angles et sont égaux.

30) Dans un repère on donne les vecteurs(2 ; 0), (1 ; 2) et (-3 ; m). Trouver m pour que les vecteurs et soient ortogonaux.

1.3 Propriété de Thalès

Mots à retenir

une configuration (конструкция, схема)

Propriété de Thalès

Soient et deux droites sécantes en A. Soient B et M deux points de , distincts de A. Soient C et N deux points de , distincts de A. Si les droites (BC) et (MN) sont parallèles alors

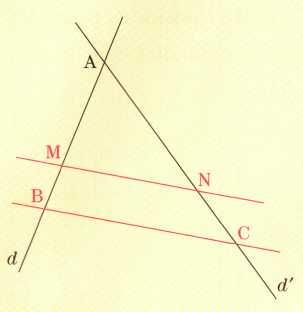Il y a deux configurations correspondant à cette propriété.

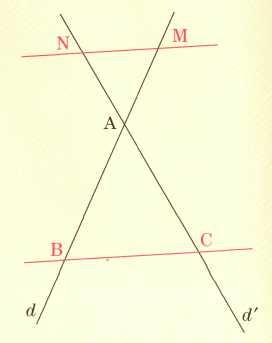
1 2

Remarque :

Si deux triangles AMN et ABC sont dans la configuration de la propriété de Thalès, les longueurs des côtés de AMN sont proportionnelles aux longueurs des côtés de ABC : AM = k AB ; AN = k AC ; MN = k BC.

Cette propriété permet de calculer une longueur.

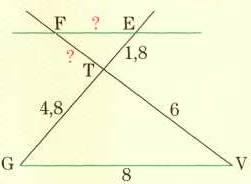
Par exemple :

Un triangle TGV est tel que  :

GV = 8 cm ;GT = 4,8cm ; TV = 6cm.

Une parallèle à la droit (GV) coupe les

droites (TV) et (TG) comme le

montre la figure ci-contre.

TE = 1,8cm. Calculer TF et EF.

Solution

1) On montre que les conditions d’application de la propriété de Thalès sont vérifiées : les droites (TG) et (TV) sont sécantes en T ; E et G sont deux points de (TG) ; F et V sont deux pointes de(TV) ; les droites (EF) et (GV) sont parallèles.

2) On applique cette propriété : d’après la propriété de Thalès

3) Les quatre longueurs connues permettent de calculer les deux longueurs inconnues : d’où