3.3 Inéquations du second degré

Mots à retenir

une réunion d’intervalles (объединение промежутков)

Définition

Une inéquation du second degré à une inconnue x est une inéquation qui peut s’écrire sous les formes : où a, b et c sont des réels donnés, avec

Méthode 1

Résoudre graphiquement en tracant la parabole d’équation dans un repère.

Par exemple : résoudre graphiquement l’équation , puis les inéquations et

Solution

La parabole représente la fonction

dans un repère.

1) Les solutions de l’équation sont

les points d’intersection de la parabole et de l’axe

des abscisses. Ce sont les nombres -1 et 3.

2) Les solutions de l’inéquation

correspondent aux points de la parabole

d’ordonnée strictement négative. Donc

l’ensemble des solutions de cette inéquationest ]-1 ; 3[.

3) Les solutions de l’inéquation correspondent aux points de la parabole d’ordonnée positive. Donc l’ensemble des solutions de cette inéquation est

Méthode 2

Pour résoudre une inéquation du second degré, on détermine le signe du trinôme associé.

• On écrit l’inéquation sous la forme (ou , ou <, ou ).

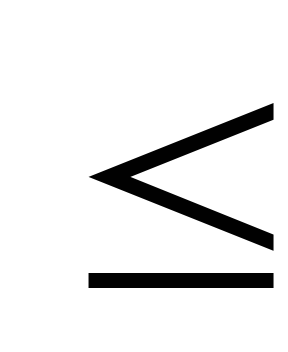• On étudie le signe de 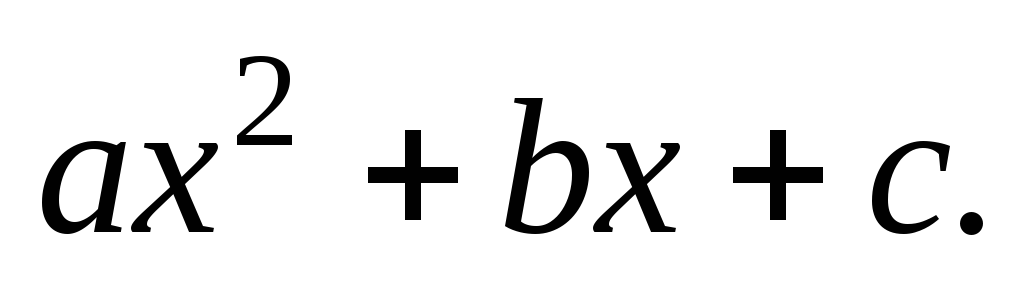Soit on résout d’abord l’équation 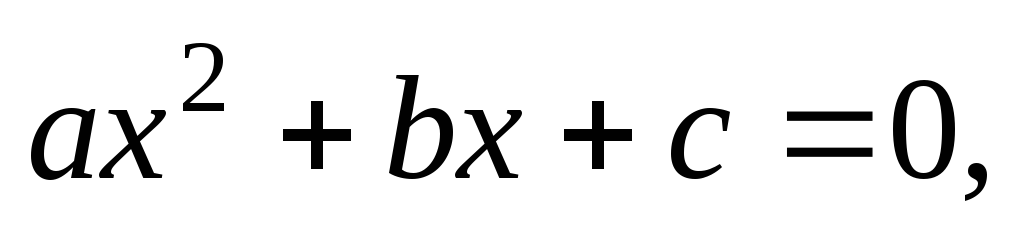on précise l’allurede la parabole donnée par le signe de a et de Δ, puis on donne le signe du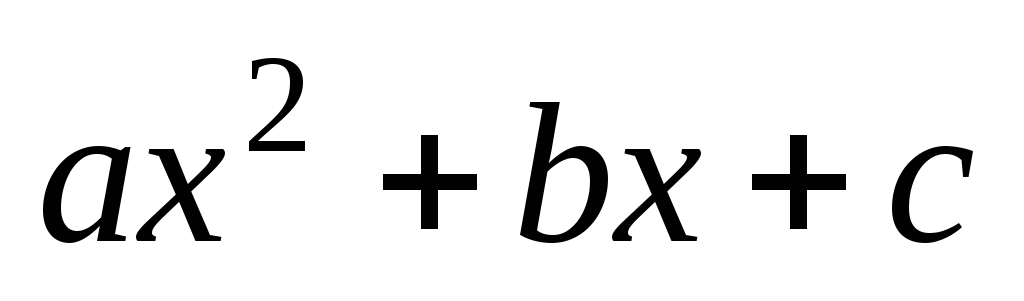selon la position de la parabole par rapport à l’axe des abscisses.

Lorsque Δ < 0, est toujours du signe de a.

Lorsque Δ = 0, est du signe de a (sauf lorsque , auquel cas)

Lorsque Δ > 0 , est du signe de a, sauf lorsque x est entre les racines, auquel cas est a sont de signes contraires .

Soit on trouve une factorisation et on étudie le signe dans un tableau.

Par exemple : résoudre l’inéquation

Solution

1) Cette inéquation s’écrit Résolvons d’abord l’équation Ici a = 1, b = -1et c = -6 ; donc Δ = 25. Δ est strictement positif, donc l’équation a deux racines : x₁ = -2 et x₂ = 3.

x	- 2 3 + ∞
	+ 0 - 0 +

Ici a > 0, donc est strictement positif, pour les valeurs de x extérieures à l’intervalle [-2 ; 3]. Pour x = 3 ou x = -2, , donc 3 et -2 sont solutions de l’inéquation. L’ensemble des solution est donc 

Réponse :

2)

On cherche le signe de chacun des facteurs puis on applique la règle des signes. On établit un tableau.

x	- ∞ -2 3 + ∞
x+2	- 0 + +
x-3	- - 0 +
	+ 0 - 0 +

L’ensemble des solution est donc

Réponse :