3. Fonction trinôme du second degré

3.1 Trinôme du second degré

Mots à retenir

un polynôme (многочлен) un trinôme (трёхчлен)

écrire (mettre) un trinôme sous la forme canonique (выделить квадрат двучлена)

Définitions

1) Si a, b et c désignent des réels avec , l’expression est appelée polynôme du second degré ou trinôme du second degré.

Ce trinôme contient trois termes :  ;  ; . On appelle terme constant le terme ne contenant pas x, c’est-à-dire c. Le terme de plus haut degré est celui dans lequel l’exposant de x est le plus élevé, c’est-à-dire

2) On appelle discriminant du trinômeou de l’équation le réel, noté Δ, défini par :

3) Toute solution de l’équation est appelée racine du trinôme.

Remarque

Le trinôme du second degré peut prendre trois formes, avec

Forme réduite Forme canonique Forme factorisée

Les deux premières existent toujours.

Par exemple :

mettre le trinômesous la forme canonique

Solution

1) On commence par mettre a en facteur. Ici a = 2. Donc ici :

2) On utilise le fait que est le début du développement de :

3) Dans l’expression , on remplace par

soit

Réponse :

Pour la forme factorisée :

• Si Δ > 0, alors 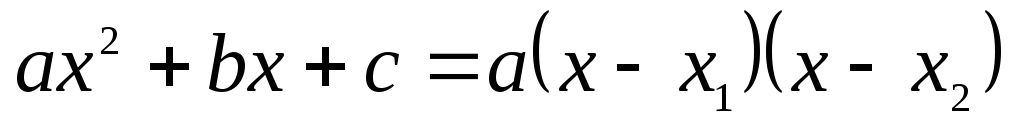, où x₁ et x₂ sont les deux racines distinctes du trinôme.

• Si Δ = 0, alors 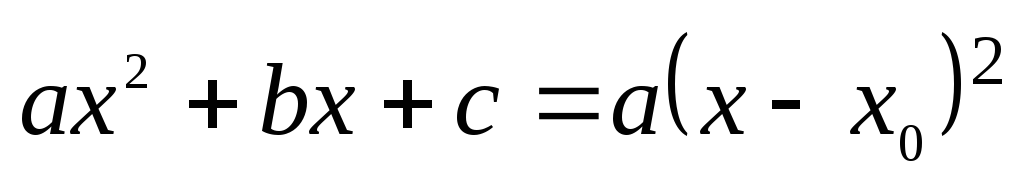, où x₀ est la seule racine du trinôme (dite « racine double »).

• Si Δ < 0, alors 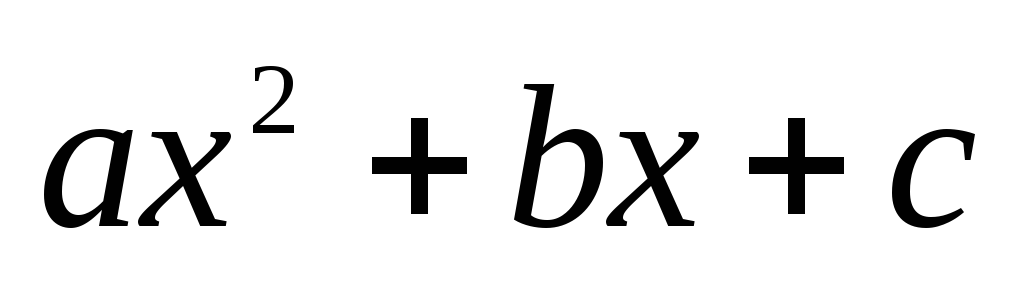ne peut pas s’écrire sous la forme d’un produit de facteurs du premier degré.

Par exemple : écrire les trinômes sous la forme factorisée

Solution

1) Ici a = 4 ; b = 8 et c = -5, donc

Puisque Δ est strictement positif, le trinôme a deux racines distinctes:

, donc donc

On peut écrire :

2) Ici a = 4 ; b = -12 et c = 9, donc

Δ est nul, donc le trinôme a une seule racine : donc

On peut écrire :

3) Ici a = 2 ; b = -1 et c = 1, donc

Puisque Δ < 0, le trinôme n’a pas de racine. La factorisation n’est pas possible.

Réponse :

le trinômene peut pas s’écrire sous la forme factorisée.

Exercices

126) Déterminer un trinôme du second degré admettant : a) les réels 2 et -5 comme racines ; b) le réel 3 comme racine double.

127) Écrire deux trinômes du second degré admettant chacun : a) -2 et 3 comme racines ; b) 2 comme racine double. 

128) Mettre les trinômes sous la forme canonique :

129) Écrire les trinômes sous la forme factorisée :

130) Écrire les trinômes sous la forme canonique :

131) Mettre les trinômes sous la forme factorisée :

132) Écrire chacun des polynômes suivants sous sa forme réduite, puis sous sa forme canonique :

133) Écrire les expressions suivantes sous la forme la plus simple :

134) Prouver que, pour tous les nombres x l’expression est positive.

135) Prouver que, pour tous les nombres x l’expression est négative.

136) Représenter les fonctions suivantes dans un repère :

137) Prouver quepour tous les nombres x.