1.3 Construire un parallélogramme
Mots à retenir
un arc (дуга) un cercle(окружность) un rayon(радиус)
le cercle de centre A et de rayon AB(окружность с центром в точке А и радиусом АВ)
par rapport à … (по отношению к)
une médiatrice (серединный перпендикуляр к отрезку)
1) Soit A, B et C, trois points non alignés, placer le point D tel que ABCD soit un parallélogramme.
Méthode 1 : tracer les côtés opposés parallèles
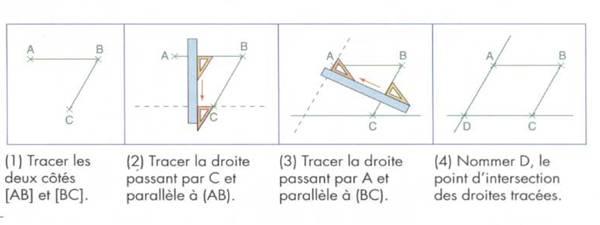On
utilise la propriété : si un quadrilatère a ses côtés
opposés parallèles alors c’est un parallélogramme.
Méthode 2 : tracer les côtés opposés de même longueur
On utilise la propriété : si un quadrilatère a ses côtés opposés de même longueur alors c’est un parallélogramme.
Méthode 3 : tracer des diagonales de même milieu
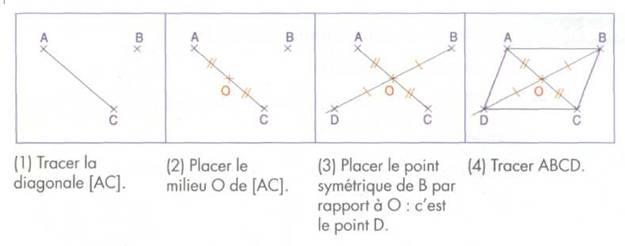On
utilise la propriété : si un un quadrilatère a ses diagonales
de même milieu alors c’est un parallélogramme.
2) Tracer deux droites perpendiculaires d1 et d2, et construire un rectangle ABCD admettant des droites d1 et d2 comme axes de symétrie.
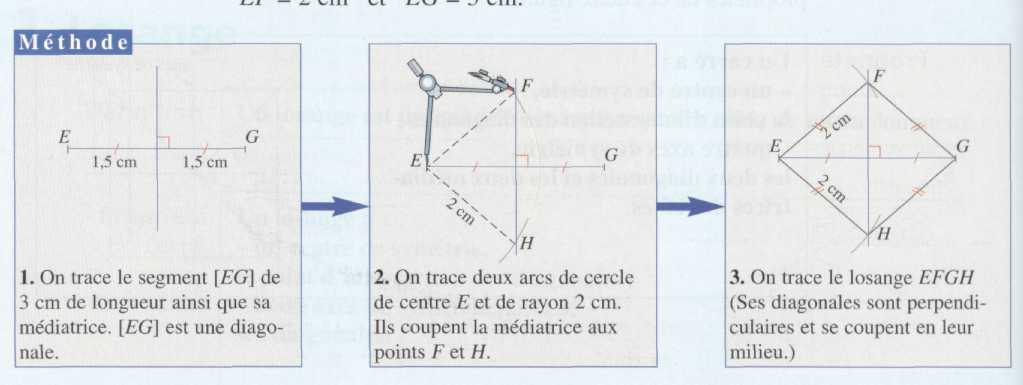
3) Construire un losange EFGH connaissant un côté et une diagonale.
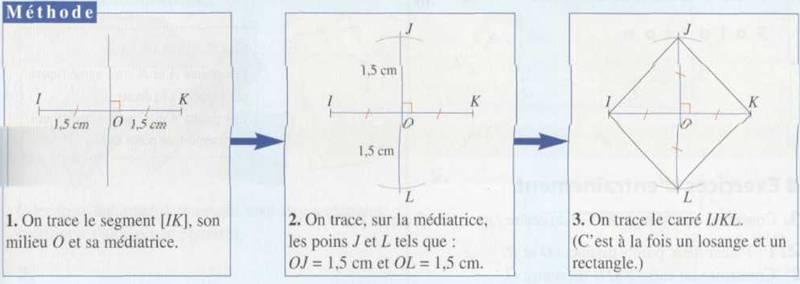
4) Construire un carré IJKL connaissant une diagonale.
Exercices
39) Tracer un parallélogramme TRFG tel que : TR = 4,5cm et TG = 3 cm.
40)
Tracer un parallélogramme UILK tel que : UI = 4,5 cm, IL = 3 cm
et
41)
Tracer un parallélogramme CVBN tel que : CV = 4,5 cm, CN = 3 cm
et
42) Tracer un losange dont les diagonales mesurent 76 mm et 43 mm.
43) Tracer un carré de 42 mm de diagonales.
44) Tracer un parallélogramme ABCD tel que : AB = 4cm et BC = 2,5cm.
45) Tracer un rectangle RSTU de 8cm de diagonale.
46) Tracer un carré IJKL de 6cm de diagonale.
47) Tracer un losange FGVC tel que : FG = 3cm et FV = 5cm.
48) Tracer, si possible : a) un parallélogramme dont les diagonales mesurent chacune 6 cm ; b) un rectangle dont une diagonale mesure 6cm et l’autre 8cm ; c) un losange dont une diagonale mesure 5cm et l’autre 4cm.
49) Tracer un parallélogramme dont une diagonale est perpendiculaire à un côté.
50) Tracer un losange de 10cm de périmètre et dont un angle 50°.
51) Tracer un parallélogramme de 24cm de périmètre et dont la longueur d’un côté est égale aux deux tiers de la longueur de l’autre côté.
52) Tracer un triangle ABC isocèle en A. Placer le point D tel que ABCD soit un parallélogramme. Quelle est la nature du triangle ADC ? Justifier la réponse.
53) Construire un losange MNOP de 22cm de périmètre et tel que MO=6cm.
54) Construire le losange ABCD de centre I tel que AI = IC = 2cm et
BI = ID = 1cm. Calculer l’aire du triangle AIB. En déduire l’aire du losange ABCD.
1.4 Trapèze
Mots à retenir
un trapèze(трапеция) une base(основание)
Définition
Un trapèze est un quadrilatère dont deux côtés sont parallèles.
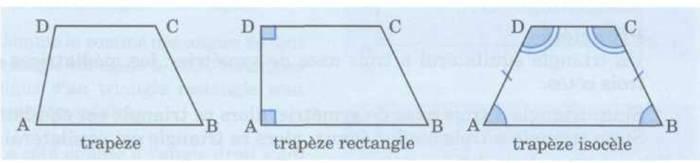Les
côtés
parallèles sont les bases.
Propriétés
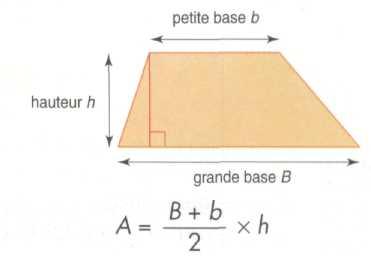
1) L’aire du trapèze est égale au produit
de la demi-somme des bases par la hauteur.
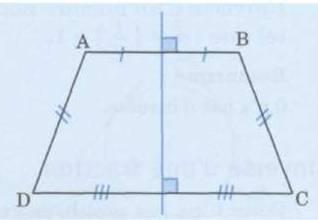
2) Un trapèze isocèle est un trapèze
dont les côtés non parallèles ont la
même longueur. Les baces ont
alors une médiatrice commune, qui
est un axe de symétrie du trapèze .