
- •Sommaire
- •4.6 Révision ......................................................................................60
- •1. Quadrilatères
- •1.1 Parallélogrammes
- •1) Diagonales
- •2) Centre de symétrie
- •Exercices
- •1.2 Parallélogrammes particuliers
- •Exercices
- •1.3 Construire un parallélogramme
- •Exercices
- •1.4 Trapèze
- •Exercices
- •1.5 Révision
- •13) Vrai ou faux ?
- •2. Racines carrées
- •2.1Racine carrée d’un nombre positif
- •Exercices
- •Exercices
- •2.3 Opérations sur les racines carrées
- •Exercices
- •2.4 Des racines carrées en géométrie
- •Exercices
- •2.5 Révision
- •3. Équations du second degré
- •3.1 Équations du second degré particulières
- •Exercices
- •Exercices
- •3.3 Les racines simples
- •Exercices
- •3.4 Révision
- •4. Généralités sur les fonctions
- •4.1 Qu’est-ce qu’une fonction ?
- •Exercices
- •4.2 Fonctions linéaires et fonctions affines
- •Exercices
- •4.3 Fonction inverse
- •Exercices
- •4.4 Fonction carré et foncion cube
- •Exercices
- •4.5 Fonction racine carrée
- •Exercices
- •4.6 Révision
1) Diagonales
O Un parallélogramme a ses diagonales qui se
coupent en leur milieu.
AO
= OC ; DO = OB et
![]()
2) Centre de symétrie
Un parallélogramme a un centre de symétrie : le
point d’intersection des diagonales.
Remarque : un parallélogramme dont les
diagonales se coupent en O est appelé
parallélogramme de centre O.
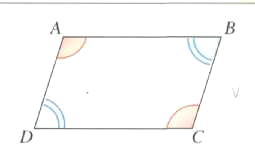
3) Angles opposés
Un parallélogramme a ses angles opposés de
même
mesure.
Donc![]() et
et![]()
4) Angles consécutifs
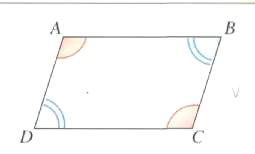 Un
parallélogramme a ses angles
consécutifs
Un
parallélogramme a ses angles
consécutifs
supplémentaires.
Donc
![]()

5) Côtés opposés
Un parallélogramme a ses côtés opposés de
même longueur.
Donc AB = CD et AD = BC.
6) Aire d’un parallélogramme
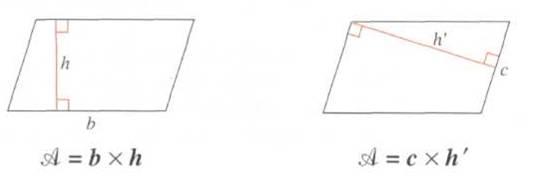 L'aire
A d’un parallélogramme est égale au produit d’un côté par la
hauteur relative à ce côté. Les longueurs doivent être exprimées
dans la même unité.
L'aire
A d’un parallélogramme est égale au produit d’un côté par la
hauteur relative à ce côté. Les longueurs doivent être exprimées
dans la même unité.
Réciproques
Ces réciproques permettent de justifier la nature d’un quadrilatère ; de reconnaître un parallélogramme ; de tracer un parallélogramme.
1) Si un quadrilatère a ses côtés opposés parallèles alors c’est un parallélogramme.
2) Si un quadrilatère a ses diagonales de même milieu alors c’est un parallélogramme.
3) Si un quadrilatère a ses côtés opposés de même longueur alors c’est un parallélogramme.
Exercices
1) On sait que MATH est un parallélogramme.
a) Nommer les côtés opposés aux côtés [AT] et [HT]. b) Nommer les diagonales.
Recopier et compléter :
c) La droite (MA) est parallèle à la droite ... .d) La droite (AT) est parallèle à la droite ... .
2)
 a)
Quels sont les sommets du quadrilatère ABCD ?
a)
Quels sont les sommets du quadrilatère ABCD ?
b) Nommer deux côtés consécutifs du quadrilatère
ABCD.
c) Nommer deux côtés opposés du quadrilatère
ABCD.
d) Nommer les diagonales du quadrilatère ABCD.
3) PQRS est un parallélogramme. Sans faire de figure, dire si les segments suivants sont des côtés ou des diagonales.
4) Construire deux parallélogrammes non superposables, dont les côtés mesurent 7 cm et 5 cm. Quel est le périmètre de ces deux parallélogrammes ?
 5)
Construire deux parallélogrammes non superposables, dont les
diagonales mesurent 7 cm et 8 cm.
5)
Construire deux parallélogrammes non superposables, dont les
diagonales mesurent 7 cm et 8 cm.
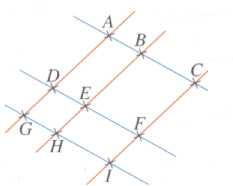
6) Sur la figure, les droites de même couleur
sont parallèles. Nommer tous les
parallélogrammes dont les sommets sont des
points marqués sur la figure.
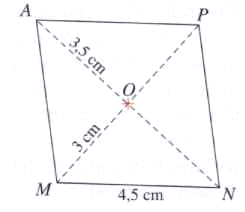 7)
Le quadrilatère MAPN est un
parallélogramme.
7)
Le quadrilatère MAPN est un
parallélogramme.
Recopier et compléter :
a) AP = ... ; b) OP = ... ; c) AN = ... .
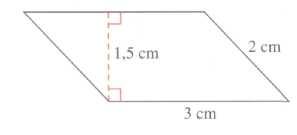
8) Construire le parallélogramme ci-dessous. Calculer son aire. Calculer son périmètre.
9) ABCD est un parallélogramme tel que AB = 6cm et AD = 5 cm. La hauteur AK relative au côté [AB] est 4 cm. Calculer l’aire du parallélogramme ABCD. Calculer la hauteur AI relative au côté [AD].
 10)
B
Sur la figure, ABCD est un
10)
B
Sur la figure, ABCD est un
parallélogramme. Les lettres x et y
représentent deux nombres.
a) Trouver le nombre x pour que le
périmètre du parallélogramme ABCD soit
égal à 24 cm.
b) x étant le nombre trouvé, trouver le nombre y pour que l’aire du parallélogramme ABCD soit égale à 28 cm.
11) Sur du papier quadrillé, tracer deux axes perpendiculaires gradués. Placer les points : A(2 ;-2) ; B(-4 ; -3) et C(-1 ; 4). En utilisant le quadrillage, placer le point D tel que ABCD soit un parallélogramme. Lire les coordonnées de ce point D.
12) Calculer l’aire du parallélogramme ABCD.
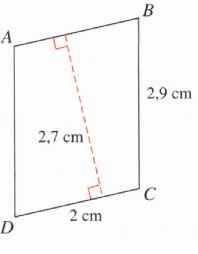
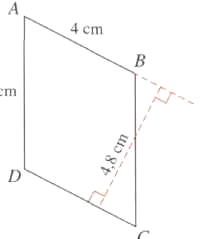 a)
b)
a)
b)
5 cm
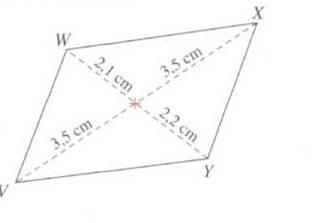 13)
Le quadrilatère VWXY est-il un parallélogramme ? Pourquoi ?
13)
Le quadrilatère VWXY est-il un parallélogramme ? Pourquoi ?
14) IJKL est un parallélogramme de centre A tel que : IJ = 4,5 cm ;
AJ = 2,6 cm ; AK = 3,8 cm. Faire une figure. Dans chaque cas, donner la longueur : a) AI ; b) IK ; c) LJ ; d) LA.
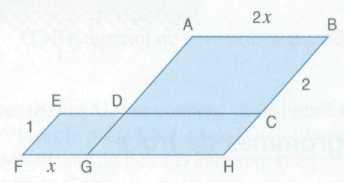 15)
15)
Calculer, en fonction de x, le
périmètre de la figure colorée :
ABCD, DCHG, EDGH sont des
parallélogrammes.
16) Placer dans un repère les points suivants : A(-1 ; 3) ; B(1 ; 5) ; C(4 ; -1).
Placer les points D, F, G tels que ABCD, ABFC, ACBG soient des parallélogrammes. Quelles sont les coordonnées des points D, F, G ?
17)
 Les
droites d1
et d2
sont parallèles
Les
droites d1
et d2
sont parallèles
ainsi que les droites d3 et d4.
a) Pour quelle raison le quadrilatère
AECB est-il un parallélogramme ?
b) Quelle est la longueur du côté [AE] ?
c) Quelle est la mesure de l’angle
![]() AEC ?
AEC ?
![]() BAE ?
BAE ?
 d)
Pourquoi I est-il le milieu de [BE] ?
d)
Pourquoi I est-il le milieu de [BE] ?
18)
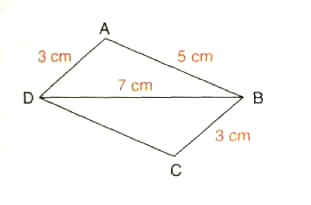
Le périmètre du quadrilatère ABCD est
de 16 cm.
a) Prouver que le quadrilatère ABCD
est un parallélogramme.
b) Citer deux angles égaux.
1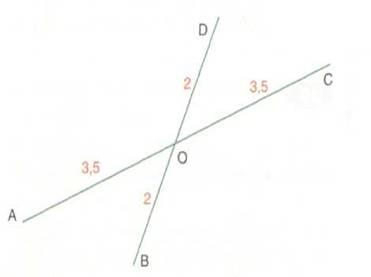 9)
9)
a) Prouver que le quadrilatère ABCD est
un parallélogramme.
b) Citer deux droites parallèles.
