4) Динамика поступательного движения материальной точки. Законы Ньютона.

Динамика – раздел механики, изучающий движение материальных тел совместно с физическими причинами, вызывающими это движение.

В основе динамики лежат законы Ньютона.

1. Закон инерции. Существуют такие СО, в которых всякое тело может находиться в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны упругих сил не изменит его состояния.

Этот закон рассматривает тело как материальную точку и выполняется только в ИСО.

Сила – физическая величина, характеризующая воздействие на данное тело со стороны других тел, вызывающее изменение движения тела.

2. Закон движения материальной точки. Импульс тела. Скорость изменения импульса материальной точки равна действующей на неё силе F:

dP/dt=F

Изменение импульса в точке за время dt равно результирующей сил.

3. Закон взаимодействия. Если одно тело воздействует на другое с некоторой силой, то и второе воздействует на первое с той же силой.

Эти силы всегда одной природы, равны по модулю, противоположны по направлению и приложены к разным телам.

5) Динамика материальной точки. Основные уравнения движения материальной точки в дифференциальной форме.

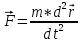
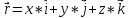
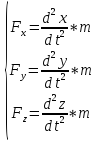
6) Динамика системы частиц, центр инерции системы, закон движения центра инерции.

Рассмотрим систему точек с массами m1,m2…m_n.

Центр масс – точка, для радиус-вектора которой выполняется:

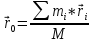
Центр масс изолированной системы находится в состоянии покоя или равномерного прямолинейного движения.

Закон движения центра масс — в инерциальных системах отсчёта центр масс системы движется как материальная точка, в которой находится масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.

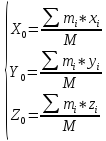
7) Динамика системы частиц, закон сохранения импульса в замкнутой системе.

В отсутствии сил импульс материальной точки остаётся неизменным по модулю и направлению (следствие из второго закона Ньютона).

Перепишем его для системы из N частиц:

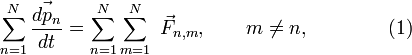
где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида и будут равны по абсолютному значению и противоположны по направлению, то есть Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:

или

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:

(постоянный вектор).

То есть суммарный импульс системы частиц есть величина постоянная.

8) Динамика переменной массы. Уравнение движения тела переменной массы. Уравнение Циолковского.

Вывод уравнения движения тела переменной массы на примере движения ракеты:

,

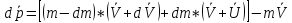Где 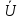- скорость истечения газов относительно ракеты. Тогда:

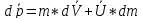
Если на систему действуют внешние силы, то изменение импульса должно быть равно импульсу внешних сил:

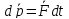
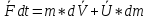
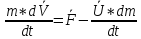
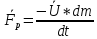
F_р – реактивная сила.

Уравнение движения тела переменной массы (уравнение И.В.Мещерского ):

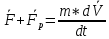
Если F=0, то:

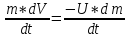
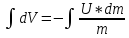
Уравнение Циалковского:

Где m₀ – начальная масса ракеты, m – конечная масса ракеты.