14. Невласні інтеграли. Ознаки збіжності.

Розглянемо функцію f:

f: [a, +)R, y[a, +) f([a, y])

Тоді визначимо функцію F:

F: [a, +)R (1)

- невласний інтеграл (НІ) 1-го роду на [a, y]. Функція f є невласно інтегрованою на [a, y].

Розглянемо ліміт функції F:

(2)

Якщо цей ліміт існує, то НІ (1) збігається.

Аналогічно вірне наступне:

f: (-, b]R, y(-, b] f([y, b])

Якщо границі (2) не існує, то інтеграл розбігається, а функція f – неінтегрована у невласному розумінні на [a, +).

Теорема 1 (Критерій Коші збіжності НІ 1-го роду)

НІ (1) збігається тоді і тільки тоді, коли для >0 y₀()0 :

f(x)0 x[a, +), тоді F(y) монотонно зростає на [a, +).

Теорема 2

Нехай f(x)0 x[a, +). Тоді для збіжності НІ 1-го роду необхідно і достатньо, щоб виконувалось:

Теорема: (рівносильні ознаки збіжності)

Якщо , то наступні умови еквівалентні:

1)

2)

3) послідовність збіжна

4) ряд -збіжн.

Теорема (практична ознака збіжності)

Якщо то розбіг

Теорема 3 (Ознака Абеля збіжності НІ 1-го роду)

Нехай:

а) - збігається;

б) функція g – монотонна та обмежена на [a, +).

Тоді невласний інтеграл - збігається.

Теорема 4 (Ознака Діріхле збіжності НІ 1-го роду)

Нехай:

а) функція f –інтегрована за Ріманом на [a, +)

б) функція g – монотонна на [a, +) та .

Тоді невласний інтеграл - збігається.

Д. Запишимо критерій Коші

за ознакою Абеля

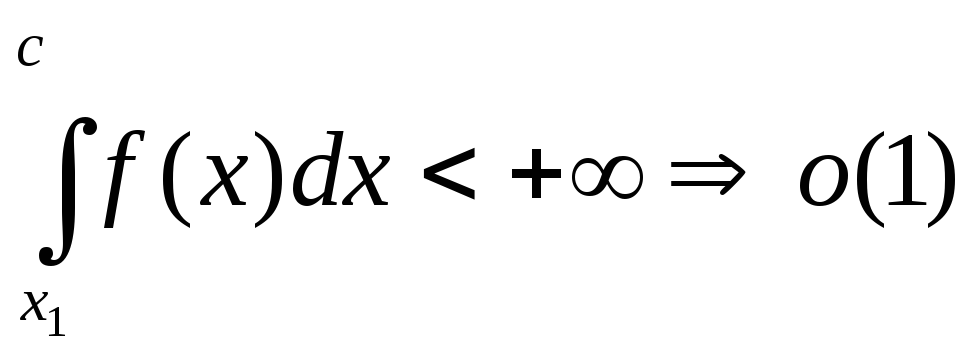за критерієм Коші

за даною теоремою доведено.

Нехай a, b – дійсні числа, -<a<b+

Визначимо функцію f: f:[a, b)R, |f(x)|+, xb-0 (b – особлива точка). f – інтегрована за Ріманом на [a, b). Тоді визначимо функцію F:

F: [a, b)R (3)

- невласний інтеграл (НІ) 2-го роду на [a, b).

Розглянемо ліміт функції F:

(4)

Якщо цей ліміт існує, то НІ (3) збігається.

Аналогічно вірне наступне:

f: (a, b]R, y(a, b] f([y, b])

Якщо границі (4) не існує, то інтеграл розбігається.

Теорема 5 (Ознака Коші збіжності НІ 2-го роду)

НІ (3) збігається тоді і тільки тоді, коли для >0 ()>0:

виконується для

f(x)0 x[a, b), тоді F(y) монотонно зростає на [a, b).

Теорема 6

Нехай f(x)0 x[a, b). Тоді для збіжності НІ 2-го роду необхідно і достатньо, щоб виконувалось:

Теорема 7 (Ознака Абеля збіжності НІ 2-го роду)

Нехай:

а) - збігається;

б) функція g – монотонна та обмежена на [a, b).

Тоді невласний інтеграл - збігається.

Теорема 8 (Ознака Діріхле збіжності НІ 2-го роду)

Нехай:

а) функція f –інтегрована за Ріманом на [a, b)

б) функція g – монотонна на [a, b) та .

Тоді невласний інтеграл - збігається.

Теорема (практична ознака збіжності )

15. Невласні інтеграли, залежні від параметра. Ознака рівномірної збіжності.

Нехай aR,YR,f:[a, +),x:YR, f(x,y)([a, A]) A>a, Y

Тоді I: YR, (1) - невласний інтеграл 1-го роду, залежний від параметра.

Розглянемо границю:

Якщо ця границя існує, то інтеграл (1) збігається. Якщо ж границі не існує, то інтеграл – розбігається.

Означення 1.

НІ (1) – рівномірно-збіжний, якщо:

(2)

(3)

Теорема 1 (необх. і дост. умова рівномірної збіжності НІ)

НІ (1) рівномірно збігається на Y тоді і тільки тоді, коли для {_n}, що визначається умовою (2), F_n, визначена в (3), рівномірно збігається до I при n.

Ця теорема напряму слідує з означення рівномірної збіжності.

Розглянемо ряд функцій:

(4)

Теорема 2.

НІ (1) збігається рівномірно на Y тоді і тільки тоді, коли збігається рівномірно на Y ряд (4), для довільної {_n}, що задовольняє умові (2).

Дов Очевидно з побудови ряду , границя при дорівнює інтегралу. Тобто будуть виконуатися усі умови означення.

Теорема 3. (Критерій Коші рівном. збіжності НІ 1-го роду)

НІ (1) збігається рівномірно на Y тоді і тільки тоді, коли:

Дов (разом з умовами теореми це задовольняє означенню рівномірної збіжності )

Теорема 4. (Ознака Вієрштраса рівном. збіжності НІ 1 роду)

Нехай f:[a, +),x:YR, g: [a, +)R задовольняють умовам:

|f(x, y)|g(x) x[a, +), yY

- збігається

Тоді НІ (1) рівномірно збігається на Y.

Доведення цього факту буде слідувати з обмеження: . Говорять, що мажоруєтья

Теорема 5. (Ознака Діріхле рівном. збіжності НІ 1-го роду)

Нехай f, g:[a, +)xYR задовольняють умовам:

g(x,y) монотонна і рівномірно прямує до 0 при x+

Тоді - рівномірно збіжний.

Теорема 6. (Ознака Абеля рівном. збіжності НІ 1-го роду)

Нехай f, g:[a, +),x:YR задовольняють умовам:

- рівномірно збіжний на Y

g(x,y) монотонна і M>0 : |g(x,y)|M xa, yY

Тоді - рівномірно збіжний

Дов Усі мажоранти не залежать від . Тому