9.Ряди Фур’є. Рівномірна збіжність рядів Фур’є.

Озн. Функція (х), яка задовольняє умову (х)=(х+Т) (Т – константа) і визначена на всій числовій осі називається періодичною функцією.

0 функції називаємо точки її неперервності, де вона = 0.

Якщо f = 0 на всій області С, за винятком, можливо, множини точок лебегової міри 0, то вона = 0 майже всюди.

Теорема: =0 f = 0 майже всюди.

E = (R([c,d]), +, , <,>)

1) майже всюди.

2)

3)

4)

- нормований простір.

- метрика

- середнє квадратичне відхилення функції f від функції g на сегменті [a,b]

Послідовність в середньому на [a,b], якщо при .

Це записують на [a,b]

Нехай на [a,b].

- функціональний ряд, Sв середньому, тоді

його можна почленно інтегрувати:

Теорема Нехай f_n - неперервно-дпфер. на [a,b]. Причому (f - неперервна); в середньому (або ) Тоді границя {f_n} f(x) є диференційовною та

Нехай f,gR([a,b])

Ф-ї f,g ортогональні, якщо .

Маємо систему ф-й

ортогональна, якщо

Нехай ортогональна система ф-й, f(x)R([a,b]), f(x)=. Припустимо, що ряд  або збігається в середньому на сегменті [a,b]. Тоді його можна почленно інтегрувати:

a_k-коеф. Фур’є функції f по ортогональній системі . - ряд Фур’є функції f по .

=, [a,b]=

, ,

- тригонометричний ряд Фур’є по основній тригонометричній системі.

Нехай - клас куск.-гладких ф-цій, визначених на .

Озн. Дві функції (х) і (х) назив-ся ортогональними на відрізку х[a, b], якщо .

В залежності від того, якою є ф-ція f(x) (парною чи непарною) ряд Фур’є може мати різний вигляд. Якщо функція f(x) – парна, то її ряд Фур’є має вигляд: .

Якщо функція f(x) – непарна, то її ряд Фур’є має вигляд: .

Умови рівномірної збіжності тригонометричного ряду (ряду Фур’є).

Озн. Функція f(x) називається кусково-неперервною на сегменті [-l, l], якщо вона неперервна в кожній точці x[-l, l], за виключенням, можливо, скінченої кількості точок, де вона має розриви першого роду.

Озн. Функція f(x) називається кусково-гладкою (кусково-диференційовною) на сегменті [-l, l], якщо вона кусково-неперервна і має неперервну похідну на цьому сегменті, за виключенням, можливо, скінченої кількості точок, в кожній з яких похідна має скінчені односторонні граничні значення.

Теорема про розклад.

Нехай кусково-гладка на сегменті [-l, l] функція f(x) періодично з періодом 2l продовжена на всю нескінчену вісь. Тоді тригонометричний ряд Фур’є функції f(x) збігається в кожній точці х(-,+) до значення . Якщо для неперервної і кусково-гладкої на сегменті [-l, l] функції f(x) виконується рівність f(-l)=f(l) , то її тригонометричний ряд Фур’є збігається рівномірно на цьому сегменті і сума ряду рівна функції f(x) в кожній точці x[-l, l].

Теорема (умови рівномірної збіжності тригонометричного ряду).

Якщо ф-я f(x) , x[-l, l], кусково-гладка на [-l, l] і на кінцях відрізку приймає рівні значення, то сума її тригонометричного ряду збігається рівномірно і , x[-l, l].

Теорема Нехай f є і . Тоді тригонометричний ряд Фур’є на .

Теорему доведемо, якщо покажемо, що збігається.

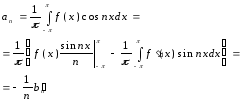
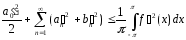
збігається збігається рівномірно.