12. Поверхневі інтеграли. Формула Гріна, Стокса, Остроградського.

Нехай Ф – гладка обмежена двостороння поверхня (якщо нормаль поверхні не змінює напрямку, то поверхня наз-ся двосторонньою). Нехай на цій поверхні задана ф-ція f(M), і крім того в кожній точці М задана функція і нормаль. Поверхню Ф розіб’ємо на n частин і в кожній частині виберемо точку М_і і складемо суму: , де – елемент площіі поверхні (величина площі і-тої ячейки розбиття Ф). Перейдемо до границі при n, тоді, якщо , то називається поверхневим інтегралом 1-го роду. Поняття поверхневого інтегралу 1-го роду поширюється і на замкнуті поверхні.

Нехай Ф – гладка двостороння поверхня. Зафіксуємо одну із сторін цієї поверхні і розглянемо вектор-функцію , задану на Ф. Позначимо через проекцію вектора F на напрямок нормалі в точці . Інтеграл називається поверхневим інтегралом 2-го роду від вектор-функції F за вибраною стороною поверхні і записують його так: . Отже, за визначенням =. При переході до іншої сторони поверхні цей інтеграл змінює свій знак на протилежний.

Формула Гріна.

Якщо функції p(X,y), q(X,y) – неперервні в замкнутій області d і мають неперервні частинні похідні в цій області і існують невласні інтеграли від кожної з функцій, то має місце формула Гріна: .

Частинні випадки формули Гріна: Q(x,y)=х, P(x,y)=-y. Тоді .

Формула Стокса.

Теорема. Нехай в деякому околі двосторонньої поверхні S функції ) – неперервні разом з своїми частинними похідними першого порядку, замкнений контур, який є межею поверхні S. Тоді має місце формула Стокса: .Орієнтація поверхні повина відповідати орієнтації кривої: .

x=x, y=y, z=z(x,y), - область, куди проектується. - межа області

вектор нормалі зад поверхні z=z(x,y): =

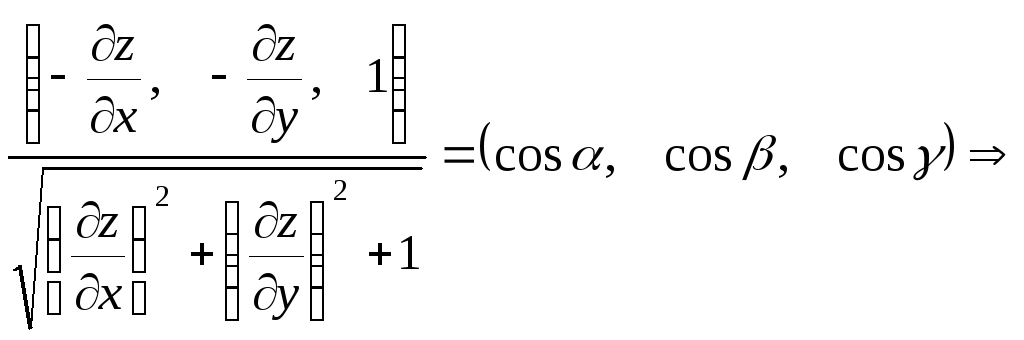
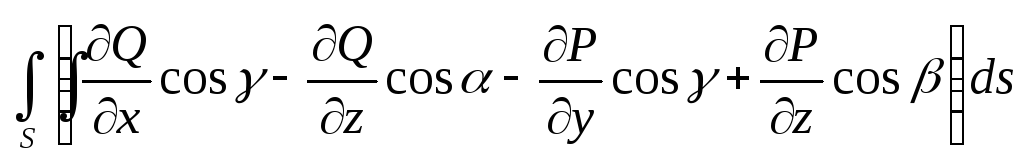=. - аналогічно першому, потім знаходимо середнє арифметичне і отримаємо нашу формулу. 

Ця формула узагальнює формулу Гріна на просторовий випадок.

Формула Остроградського.

Теорема. Функції ) – неперервні в замкнутій області V разом зі своїми похідними , тоді :, S–поверхня, яка обмежує об’єм V, n- вектор нормалі до зовнішньої сторони, - вектор ф-я.

.

 - доведемо. Розіб’ємо елем тіло на скінч кількість елем тіл для інтегр по x, y. Всі межі мають Лебегову міру 0, отже на інтеграл не впливають, всі інт по внутр поверхні =0. Достатньо довести формулу для тіла елем для інтегрув по x,y.

, ,

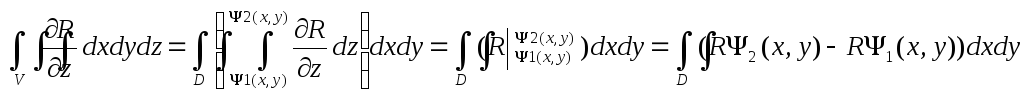=|=0,s1-верхня основа,s2-нижня основа,s3-бічна поверхня.|=. 

13.Градієнт, дивергенція та вихор векторного поля.

Озн. Говорять, що задане скалярне поле, якщо кожній точці М простору поставлено у відповідність деяке число f(M). Якщо кожній точці М простору поставлено у відповідність деякий вектор R(M), то говорять, що задане векторне поле.

Поняття градієнту. Нехай (М) – скалярне поле, визначене в області V простору (x, y, z), (l) – довільна крива, що лежить в V і проходить через фіксовану точку , l – довжина дуги кривої (l) від точки M₀ до точки М. Якщо існує скінчена границя відношення при , то вона називається похідною поля (М) в точці M₀ вздовж лінії (l) і позначається символом : . Якщо ф-ція (М) диференційовна в точці M₀ , то її похідна вздовж лінії (l) існує і для всіх ліній, що виходять з точки M₀ , з однією і тією ж дотичною величина цієї похідної одна і та ж, а сама похідна називається похідною за даним напрямком  і обраховується за формулою: . Вектор називається градієнтом. Він спрямований із точки M₀ в бік найшвидшого зростання ф-ції (М), а за абсолютною величиною рівний похідній поля (М) в цьому напрямку.

.

Поняття дивергенції. Нехай S – скінчена гладка поверхня, а R(M) – довільне векторне поле, задане в деякій області V, що містить всі точки поверхні S. Якщо поверхня S, що обмежує об’єм V, замкнена і існує границя при стягуванні об’єму V в точку Р, (де – потік векторного поля) , то ми називаємо її дивергенцією поля R в точці Р і позначаємо div R(P): . Таким чином за визначенням дивергенцією є щільність адитивної функції областей – потоку векторного поля R через замкнену поверхню S.

Поняття вихора векторного поля. Нехай R(M) – довільне векторне поле, задане в скінченій області V з гладкою границею S, n(M) – одиничний вектор зовнішньої нормалі до поверхні S в точці M . Вектор-функція називається циркуляцією поля R(M) по межі області V. Якщо існує границя при стягування об’єму V в точку Р , то вектор q(P) називається вихорем, чи ротором поля R(M) в точці Р і позначається rot R(P): . Таким чином, за визначенням вихор – це щільність адитивної функції областей – циркуляції векторного поля по його межі області.