
- •1. Числова послідовність та її границя.
- •2. Границя і неперервність функції у розумінні Коші та Гейне.
- •Виберемо довільне c між a і b. Позначимо . (в деякій точці)
- •4. Диференційованість функціі. Критерій диференційованості.
- •5. Локальний екстремум. Необхідні та достатні умови екстремуму.
- •6.Інтеграл Рімана. Критерій інтегровності функції за Ріманом.
- •7. Числові ряди. Ознаки збіжності.
- •8. Функціональні ряди. Ознаки рівномірної збіжності.
- •9.Ряди Фур’є. Рівномірна збіжність рядів Фур’є.
- •Теорема про розклад.
- •10. Інтеграл Рімана на компакті. Подвійний, потрійний інтеграл Рімана.
- •11.Криволінійні інтеграли Умови незалежності криволінійних інтегралів від шляху інтегрування.
- •12. Поверхневі інтеграли. Формула Гріна, Стокса, Остроградського.
- •Якщо функції p(X,y), q(X,y) – неперервні в замкнутій області d і мають неперервні частинні похідні в цій області і існують невласні інтеграли від кожної з функцій, то має місце формула Гріна: .
- •13.Градієнт, дивергенція та вихор векторного поля.
- •14. Невласні інтеграли. Ознаки збіжності.
- •Теорема 6
- •15. Невласні інтеграли, залежні від параметра. Ознака рівномірної збіжності.
- •16. Формула Тейлора.
- •17. Функції багатьох змінних. Диференціал та частинні похідні.
10. Інтеграл Рімана на компакті. Подвійний, потрійний інтеграл Рімана.
Позначимо
![]() ,
,
![]() ,
,
![]() .
.
Озн.
Верхньою (нижньою) інтегральною сумою
Дарбу для функції f:[a,b]®R
і розбиття Р називається і позначається
сума
![]() (
(![]() )
.
)
.
Озн.
Верхнім (нижнім) інтегралом Дарбу
для функції f на [a,b] називається і
позначається вираз:
![]() (
(![]() ).
).
Озн.
Функція назив-ся інтегровною за Ріманом
на [a,b], якщо її
![]() =
=![]() ,
при цьому спільне значення цих інтегралів
називається інтегралом Рімана на [a,b].
,
при цьому спільне значення цих інтегралів
називається інтегралом Рімана на [a,b].
До класів інтегровних функцій можна віднести:
-
неперервні ф-ції, інтегровні на [a,b].
-
Ф-ції, що мають злічене (скінчене) число точок розриву 1-го роду.
-
Всі монотонні ф-ції на [a,b].
Властивості кратних інтегралів:
-
Якщо відрізок [a,b] рівний 0, то
 .
. -
 .
. -
 .
. -

-
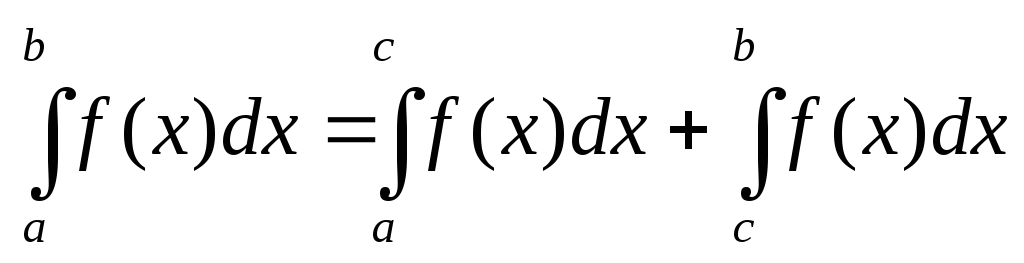
-
Якщо ф-ції f,g – інтегровні, то добуток цих ф-цій теж інтегровний.
-

-
 .
.
Правила інтегрування:
Як
правило використовується формула
Ньютона-Лейбніца:
![]() (Ф – первісна).
(Ф – первісна).
Є 2 методи інтегрування:
-
метод інтегрування частинами
 ;
; -
метод підстановки
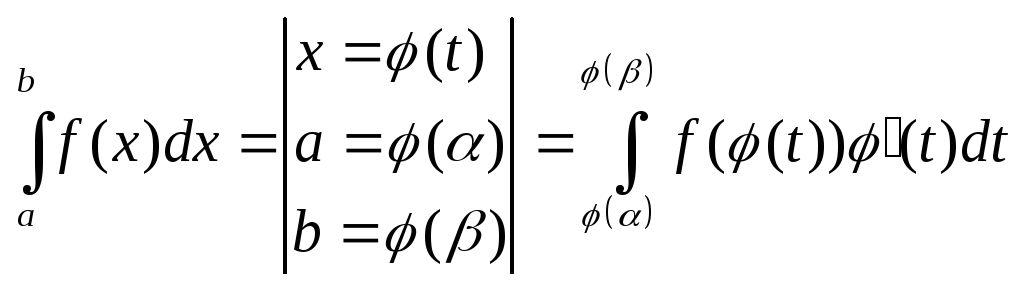 .
φ(t) – диференційовна і неперервна,
a≤φ(t)≤ b.
.
φ(t) – диференційовна і неперервна,
a≤φ(t)≤ b.
Застосування інтегралів Рімана:
-
Обчислення площи криволінійної трапеції.
Нехай
![]() ,
,
![]()
![]()
![]()
![]() накладаються умову
накладаються умову
![]() .
Ці умови задають криволінійну трапецію,
площа для якої обчислюється за формулою
.
Ці умови задають криволінійну трапецію,
площа для якої обчислюється за формулою
![]()
-
Площа криволінійного сектора:
![]() -
криволінійний сектор. Площа дорівнює
-
криволінійний сектор. Площа дорівнює![]() .
.
-
Параметрично задана крива:
![]() ,
,![]() сама крива не має самоперетинів та
розривів при обході за годинниковою
стрілкою.
сама крива не має самоперетинів та
розривів при обході за годинниковою
стрілкою.
![]()
-
Обьєм тіла при обертанні
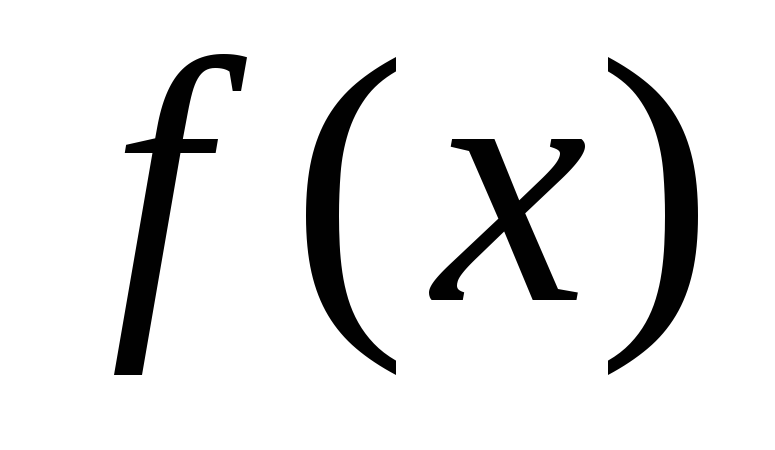 навколо
вісі
навколо
вісі
 :
:
![]() ,
,![]() ,
,![]() ,
,![]() - тіло утворене при обертанні.
- тіло утворене при обертанні.
![]()
-
При обертанні навколо
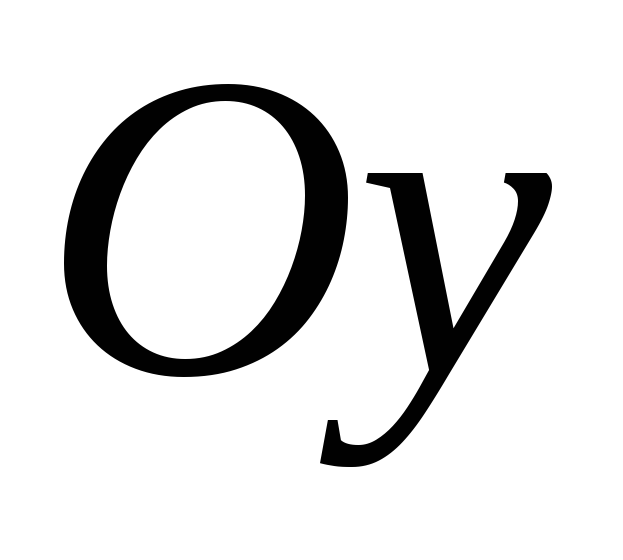 так само, лише додаткова умова
так само, лише додаткова умова
 - монотонна.
- монотонна. -
Довжина параметрично заданої кривої:
![]() ,
крива задається за 3) плюс
,
крива задається за 3) плюс
![]() ,
,
![]()
![]()
![]()
Подвйний інтеграл.(обчислення кратних інтегралів Рімана для паралелепідальних областей)
Нехай
потрібно обчислити інтеграл:
![]() (D – прямокутник:
(D – прямокутник:
![]() .
Інтегрування кратних інтегралів
зводиться до обчислення повторних
інтегралів) =
.
Інтегрування кратних інтегралів
зводиться до обчислення повторних
інтегралів) =![]() .
Це основна формула зведення кратного
інтегралу до повторного. Коли обчислюємо
внутрішній інтеграл по якійсь змінній,
то інша змінна виступає як параметр
(стала).
.
Це основна формула зведення кратного
інтегралу до повторного. Коли обчислюємо
внутрішній інтеграл по якійсь змінній,
то інша змінна виступає як параметр
(стала).
Потрійний інтеграл.
Нехай V –якийсь об’єкт, кубоване тіло. Потрібно по V обчислити інтеграл.
![]()
![]() =
=![]()
11.Криволінійні інтеграли Умови незалежності криволінійних інтегралів від шляху інтегрування.
-
проста гладка крива(траекторія), якщо
існує непер.-диф.
![]() де
де
![]() -
параметричне зображення і
-
параметричне зображення і
![]() -
похідна не рівна 0.
-
похідна не рівна 0.
Нехай
![]() - інше параметричне зображення. Тоді
- інше параметричне зображення. Тоді
![]() і
і
![]() .
Отже існує композиція
.
Отже існує композиція
![]() ,
причому
,
причому
![]()
Озн
Якщо![]() то параметричне зображення
то параметричне зображення
![]() та
та
![]() - еквівалентні. При цьому множину усіх
еквівал. зображень простої гладкої
кривої
- еквівалентні. При цьому множину усіх
еквівал. зображень простої гладкої
кривої
![]() позначимо
позначимо![]()
Озн
Упорядкована пара
![]() - орієнтована проста гладка крива Г.
- орієнтована проста гладка крива Г.
![]() утворюють
утворюють
![]() - протилежно орієнтована Г.
- протилежно орієнтована Г.
Озн
Криволінійний інтеграл I роду
![]() де dl - диференціал довжини дуги
де dl - диференціал довжини дуги
![]() .
.
![]()
Розуміємо:
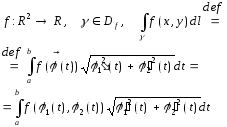
Озн
Множина
![]() -
проста гладка крива, якщо існує неперервне
-
проста гладка крива, якщо існує неперервне
![]() і
і
![]() де
де
![]() - параметричне зображення
- параметричне зображення
![]() .
.
Озн
Якщо
![]() - інше параметричне зображення, то
- інше параметричне зображення, то
![]() і якщо
і якщо
![]() то параметричне зображення
то параметричне зображення
![]() та
та
![]() - еквівалентні. При цьому множину усіх
еквівал. зображень простої гладкої
кривої
- еквівалентні. При цьому множину усіх
еквівал. зображень простої гладкої
кривої
![]() позначимо
позначимо
![]()
Озн
Упорядкована пара
![]() - орієнтована проста гладка крива Г.
- орієнтована проста гладка крива Г.
![]() - протилежно орієнтована Г.
- протилежно орієнтована Г.
Озн
Криволінійний інтеграл I роду
![]()
Розуміємо:

Нехай
![]() -
орієнтована гладка проста крива.
-
орієнтована гладка проста крива.
![]() .
.
Озн Криволінійний інтеграл II роду
![]()
Теорема
Нехай
![]() -
непер. разом із
-
непер. разом із
![]() у замкненій однозв’язній області G.
Тоді наступні умови еквівалентні:
у замкненій однозв’язній області G.
Тоді наступні умови еквівалентні:
-
 для
довільного замкнутого контура
для
довільного замкнутого контура
 .
. -

 не
залежить від вибору шляху інтегрування
( тобто визнач. початкові
і кінцеві точки інтегрування).
не
залежить від вибору шляху інтегрування
( тобто визнач. початкові
і кінцеві точки інтегрування). -
W=Pdx+Qdy є повним диференціалом деякої ф-ції.
-
 ,
,

1![]() 2.
Розглянемо 2 шляхи (
2.
Розглянемо 2 шляхи (![]() )
і покажемо ,що
)
і покажемо ,що
![]() .
Утворимо контур
.
Утворимо контур
![]()
0=![]() .
.
2![]() . Зафіксуємо
. Зафіксуємо
![]() і визначимо
і визначимо
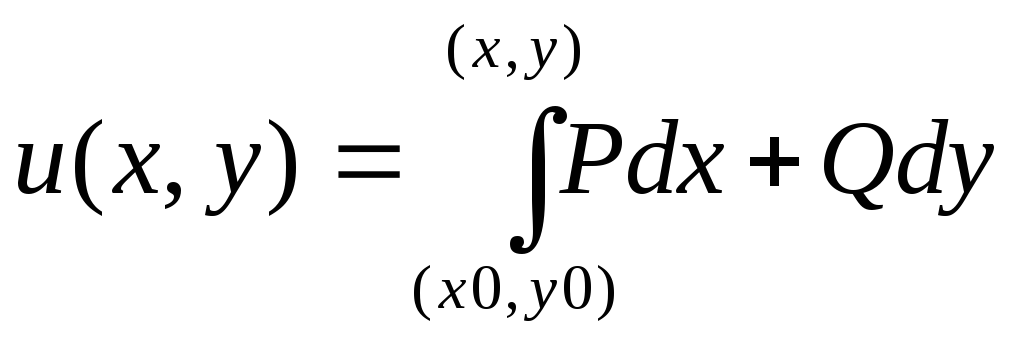 .
З умови 2 функція u
визначена однозначно ,
покажемо, що задовольняє умову3. Розглянемо
.
З умови 2 функція u
визначена однозначно ,
покажемо, що задовольняє умову3. Розглянемо
 за
теор про середнє
за
теор про середнє
![]() ,
,
![]() ,
,
![]() .
.
![]() , аналогічно
, аналогічно
![]() .
.
3![]() . З теореми про рівність мішаних похідних
. З теореми про рівність мішаних похідних
![]() ,
,
![]() .
З того,що вони існують і неперервні вони
рівні між собою, отже
.
З того,що вони існують і неперервні вони
рівні між собою, отже
![]() .
.
4![]() . Розглянемо довільний замкнений контур
. Розглянемо довільний замкнений контур
![]()
(з властивості 4).
Теорема:
(незал крив інт від шляху інтегрування
в
![]() )
)
Нехай
V – замкнена,
поверхневооднозв’язна область в
![]() ,
на V визначена
функція f
,
,
на V визначена
функція f
,
![]() ,
що є неперервною на V
разом з похідними
,
що є неперервною на V
разом з похідними
![]() ,
тоді наступні умови еквівалентні:
,
тоді наступні умови еквівалентні:
-
Інтеграл по замкненому контуру =0.
-
Інтеграл не залежить від шляху інтегрування.
-
 -
неперервна диф-на ф-я :
-
неперервна диф-на ф-я :
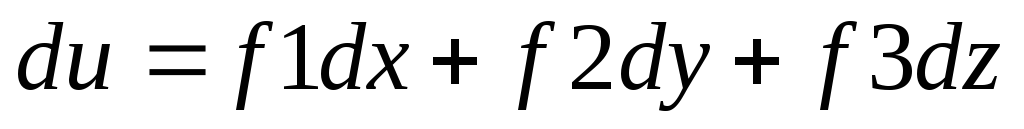 .
. -
 .
.
