Как избежать локальных минимумов

Для MLP-mnSOM, локальные минимумы являются причиной серьезных проблем, потому что модули, которые попали в локальные минимумы, разрушают непрерывность карты в этих точках. Что еще хуже, вероятность попадания в локальный минимум увеличивается, при увеличении числа модулей. Поэтому необходим дополнительный алгоритм для предотвращения попадания в локальные минимумы.

Как показано в (7), задача k-го модуля состоит в сведении к минимуму функции энергии . Это означает, что должен минимизировать среди всех модулей. Теперь предположим, что модуль временно заменен другим модулем . Если функция энергии возрастает после замены, то это может быть обосновано тем, что , вероятно, попал в локальный минимум. В таком случае, может быть «спасен», копированием в . Этот алгоритм формулируется следующим образом:

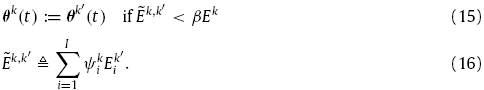
Здесь – это функция энергии, когда временно заменен на , а – фактор безопасности, который обычно задается около 0,8–0,9. Делая такие сравнения между соседями, перед адаптивным процессом, модуль MLP в локальном минимуме переводится в лучшее начальное состояние, заданное соседями, и после этого модуль меняется в сторону своего собственного глобального минимума.

Используя этот дополнительный алгоритм, вероятность попадания в локальный минимум будет уменьшаться с увеличением количества модулей, поскольку шанс «спасения» также увеличивается. Поэтому этот алгоритм превращает недостаток большого количества MLP-модулей в преимущество. Кроме того, этот алгоритм не имеет отрицательных последствий, так как совсем не изменяет функцию энергии. Соседи только протягивают руку помощи модулю, попавшему в беду, давая лучшую точку для перезапуска модуля. Сразу после ухода из локального минимума, модуль может быть обновлен в сторону своей цели, которая отличается (но похожа) от целей его соседей. Таким образом, алгоритм увеличивает шансы на успех, не влияя на успешные результаты.

Базовая версия

Слой Кохонена состоит из некоторого количества n параллельно действующих линейных элементов. Все они имеют одинаковое число входов m и получают на свои входы один и тот же вектор входных сигналов x = (x1,...xm). На выходе jго линейного элемента получаем сигнал

где w_ij— весовой коэффициент i-го входа j го нейрона, w_0j — пороговый коэффициент.

После прохождения слоя линейных элементов сигналы посылаются на обработку по правилу «победитель забирает всё»: среди выходных сигналов y_j ищется максимальный; его номер jmax = argmaxj{y_j}. Окончательно, на выходе сигнал с номером jmax равен единице, остальные — нулю. Если максимум одновременно достигается для нескольких jmax, то либо принимают все соответствующие сигналы равными единице, либо только первый в списке (по соглашению). «Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них.»

Связь между mnSom и som

Как отмечалось в теоретической части, алгоритм mnSOM это не просто модификация обычной SOM, а обобщение, включающее в себя обычную. Таким образом, mnSOM не только наследует многие свойства обычных SOM, но и также добавляет некоторые новые оригинальные свойства. Поэтому, важно понять, в чем сходства и различия между SOM и mnSOM. Например, не ясно, наследует ли mnSOM статистические свойства обычных SOM.

Для этой цели мы должны вновь рассмотреть случай кубических функций. В разделе моделирование, mnSOM была создана карта особенностей семейства кубических функций на основе набора входных-выходных данных. Данные были отобраны случайным образом из этих функций, и они были представлены mnSOM в случайном порядке. Практически, этот способ обучения очень естественен для реальных проблем, таких, как в случай с погодными данными. Однако, в искусственной ситуации, как в случае кубических функций, также можно векторизовать формы функций, т.к. экспериментатор знает эти функции заранее (конечно, такая информация не предоставляется mnSOM). Это означает, что карта особенностей семейства кубических функций может быть также создана обычной SOM. Тогда возникает один вопрос: существует ли разница между картой особенностей, созданной mnSOM и порожденной обычной SOM? Чтобы ответить на этот вопрос, рассмотрим случай, когда для векторизации применяется ортонормированное функциональное расширение. Таким образом, пусть будет набором ортонормированных функций. Функция преобразуется в вектор коэффициентов , где

Термы порядка выше n считаются незначительными. При этом условии, расстояние в функциональном пространстве совпадает с расстоянием в пространстве векторов коэффициентов. Таким образом,

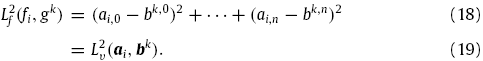
Здесь, и квадраты расстояний в функциональном и векторном пространствах, а и обозначают векторы коэффициентов i-й функции и k-го модуля mnSOM соответственно. В этом случае, mnSOM и SOM должны давать один и тот же результат, поскольку алгоритм обучения, т. е. (1)–(9) одинаковы для обоих типов SOM. То есть, mnSOM и обычная SOM выделяют одни и те же свойства карты особенностей. Этот означает, что множество рранних работ по обычным SOM могут быть применены к MLP-mnSOM.

Карта погоды области Кюсю, созданная mnSOM.

В случае кубической функции, p(x) была равномерной на интервале [-1,+1]. Поэтому, нормированные многочлены Лежандра лучше всего подходят для ортонормированного расширения в этом случае. Таким образом, n-ая ортонормальная функция описывается n-ой функцией Лежандра , как

Используя этот набор ортонормированных функций, набор из шести функций, обозначенных толстыми рамками на рис. 2 был расширен до соответствующих векторов коэффициентов . Карта особенностей, созданная обычной SOM для показана на рис. 9 (a). На рисунке показано положение каждого вектора в пространстве векторов коэффициентов. Соответствующая карта созданная mnSOM показана на рис. 9 (b) и (c). Рис. 9 (b) показывает карту точек глобального минимума каждого MLP-модуля рассчитанного по (8). Говоря простыми словами, это можно рассматривать как «карту сигналов учителя», созданную mnSOM. Между тем, рис. 9 (c) это карта самих функций, полученных MLP-модулями mnSOM. Таким образом, рис. 9 (c) был получен путем разложения Лежандра функций, изображенных на рис. 4 (a). Карта, порожденная обычной SOM и карта обучающих сигналов mnSOM (рис. 9 (a) и (b)) были идентичны, как это утверждалось в теории. Карта самих функций MLP-модулей (рис. 9 (с)) также довольно похожа на две другие карты, но небольшие ошибки сохранились, что предположительно вызвано аддитивным шумом и ограничением возможностей аппроксимации MLP-модулями. Средняя квадратичная ошибка выходов, между идеальным результатом, полученным SOM (рис. 9 (a)) и фактическим выходом mnSOM с аддитивным шумом (рис. 9 (c)) составила . Эта ошибка примерно соответствует 3% выходного диапазона, в то время как обучающая выборка содержит 4% шума. Эти результаты могут вдохновить использование mnSOM потому что теоретические свойства MLP-mnSOM были проверены в прошлых работ, проведенных на обычных SOM. Это также означает, что все преимущества и недостатки обычных SOM также унаследованы mnSOM, такие, как сложность задания функции энергии.

Наконец, стоит отметить, что такое ортонормированное расширение не возможно до обучения в большинстве случаев на практике, где отображаемые объекты неизвестны. Таким образом, обычные SOM не могут применяться в таких случаях. С другой стороны, mnSOM может решить задачу одновременной оценки нескольких неизвестных функций и создания их карты. Это еще одно важное преимущество mnSOM.

Проектирование модулей

Можно поставить вопрос о том, как алгоритм mnSOM должен быть спроектирован, когда пользователь использует новые типы модулей. Поскольку существует множество архитектур и алгоритмов, разработка обобщенного протокола кажется безнадежной задачей. К счастью, однако, меры расстояний или функцмм энергии часто идут вместе с архитектурой модуля. Поэтому все, что должен сделать пользователь, это заменить функцию энергии на (12). Для минимизации функции энергии, также возможно использовать эволюционные алгоритмы и метод градиентного спуска.

О разработке модулей mnSOM и алгоритмов их обучения, пользователям необходимо знать следующие два момента. Во-первых, пользователям следует помнить о согласовании между их целью, архитектурой модуля, и алгоритмом. Чтобы лучше объяснить это, рассмотрим случай, когда два пользователя mnSOM пытаются создать карту из набора данных временных рядов. Предположим, что один пользователь пытается сделать карту сигналов, а другой хочет,получить карту динамики. В таком случае, первому пользователю необходимо определить меру расстояния в пространстве сигналов, в то время как второй должен определить её в системном пространстве. Кроме того, выбор модульной архитектуры и алгоритма должен соответствовать их цели. Пользователи должны быть аккуратны, т. к. небольшое изменение динамики системы вызывает большие изменения формы сигналов. mnSOM создаст подобие карты, даже если мера расстояния и алгоритм не определены надлежащим образом. Однако, нет никакой гарантии, что созданная в этом случае карта будет соответствовать целям пользователя. Таким образом, согласованность определений и цели пользователя должна быть проверена в любом случае. Один из лучших способов, это проверить, создает ли алгоритм желаемые «промежуточные» объекты для задач пользователя. Путем подачи двух объектов A и B на один модуль с весами и , пользователь может увидеть, представляет ли модуль промежуточный объект между A и B. Только пользователь знает, каким должен быть промежуточный результат и, следовательно, принять эту обязанность в качестве компенсации за свободу предоставляемую mnSOM.

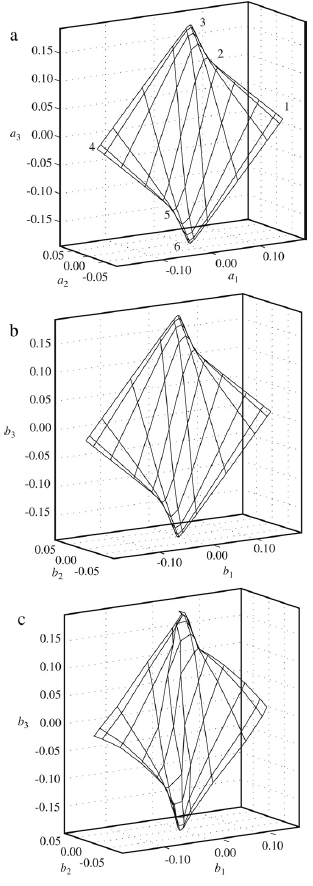
Карта особенностей кубических функций построенных в пространстве коэфициентов разложения Лежандра. (a) Карта созданная обычной SOM. Метки 1-6 представляют лучшие модули для обучающих функций, отмеченных толстыми рамками на рис. 2. (b) «карта обучающих сигналов», созданная mnSOM. (c) карта фактических функций, полученная MLP-модульной mnSOM.

Второй момент заключается в том, что пользователям рекомендуется проверять параметры модулей, прежде чем встраивать их в mnSOM. Таким образом, лучше заранее проверить способности одного модуля на одном классе данных, т. к. mnSOM обычно имеет множество параметров, которые требуют корректировки. Как только пользователь находит подходящий набор параметров для одного модуля, то остальные параметры почти такие же, как и для обычной SOM. Таким образом, пользователи не будут испытывать затруднений в настройке параметров, если используют этот двухступенчатый метод настройки.

В данной работе, случай MLP-модулей был представлен как наиболее показательный, т. к. MLP это одна из наиболее популярных архитектур нейронных сетей и алгоритм градиентного спуска также распространен. Для практических задач, однако, другие архитектуры, такие как RBF сети должны давать лучшие результаты.