Весна 17 курс 4 ОрТОР / Конструкция и прочность ВС / Новая папка / KiPVS

- R1'' и R2'' - реакции опор от несимметричных нагрузок (сил и моментов), действующих на крыло (Yэ).

R= 0,5 × (qk + q0) × lk = 0,5 × (8201,1 + 3089) × 15,375 = 86 793 Н

R1' = R2' = 86793 Н

Реакции опор найдены, можно переходить к построению эпюр изгибающего момента Mu, поперечной силы Q и крутящего момента Mкр.

4.3 Построение эпюр поперечных сил, изгибающих и крутящих моментов

Построение эпюр произведем раздельно: для всегда симметричных нагрузок qz ;

Затем на них накладывать (с учетом знаков) эпюры от несимметричных сосредоточенных, а потом уже – эпюры от несимметричных сил.

Распределенная нагрузка q, поперечная сила Q и изгибающий момент Ми связаны между собой интегральными зависимостями:

22

Подставив qz в первое уравнение (3.46) и решив последовательно первое и второе, получим:

Для упрощения расчетов, замени в формулах (4.3 и 4.4) постоянный сомножитель и вычислим

Где:

- Gk – масса крыла, равная:

=× ;

= 6540×9,81 = 64157,44[ ];

- GТ – масса топлива, равная:

Расчет значений поперечной силы Q(qz ) удобно свести в таблицу:

24

Крутящий момент Мк возникает тогда, когда сила не проходит через центр жесткости крыла. Общий крутящий момент получается непрерывным суммированием (интегрированием) всех погонных крутящих моментов:

0,12×451338,89+3,07×(64157,44+136113,75) = 1004,24 127,4

Расчет значений крутящего момента Мк тоже оформим в виде таблицы; Таблица 4

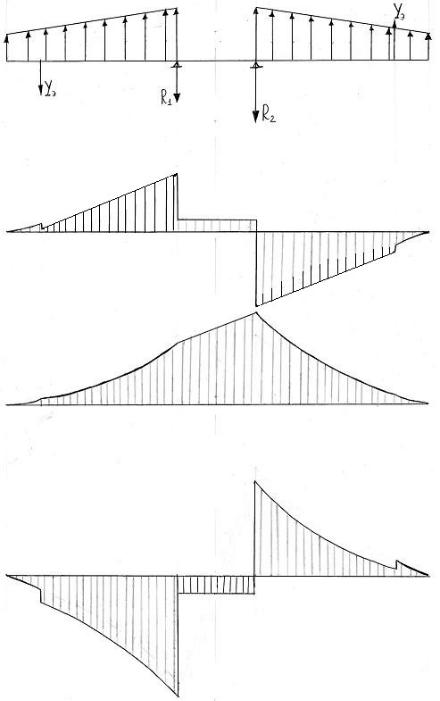
25

Рис. 7. Эпюры перерезывающих сил, изгибающего и крутящего моментов

26

5. АНАЛИЗ И ПОДСЧЕТ ФАКТИЧЕСКИХ НАПРЯЖЕНИЙ

Критерием работоспособности конструкции (крыла, фюзеляжа или др.), то есть близости ее к состоянию разрушения или необратимых деформаций, является величина напряжений, возникающих в силовых элементах конструкции от действия на неё эксплуатационных нагрузок: изгибающего, крутящего моментов и поперечной силы.

По эпюрам MИ ,MK ,Q определяем наиболее нагруженное сечение, где моменты и поперечная сила максимальны. Если их максимумы не совпадают(не находятся в одном сечении),

то расчет проводится для сечения с максимальным MИ .

Схематизируем сечение крыла в соответствии с реальным расположением силовых элементов.

Силовой частью сечения крыла является межлонжеронная часть, длинна и высота которой

равны:

Где:

-B - длина межлонжеронной части;

-H - высота межлонжеронной части;

-bz - текущая хорда крыла;

-с - относительная толщина крыла.

Поперечное сечение (расчетное) прямоугольное однозамкнутое, то есть имеет два лонжерона, верхнюю и нижнюю обшивку (рис. 9):

Рис. 8. Напряжения в силовых элементах сечения крыла, возникающие

от внешних сил Q ,MИ ,MK

Крыло является тонкостенной замкнутой конструкцией, основные силовые элементы которой сосредоточены в верхней и нижней панелях (обшивка, стр ингеры, полки лонжеронов). При изгибе, например, вверх (от аэродинамических сил) верхняя панель сжимается, нижняя растягивается, то есть обе работают на нормальные напряжения; при этом изгибающий момент трансформируется в пару сил:

а напряжения от них будут равны:

Где:

-FВП - площадь верхней панели крыла;

-FHП - площадь нижней панели крыла.

Площадь панели определяется площадью обшивки, площадями всех стрингеров и полок лонжеронов (переднего и заднего). Т.е.:

Где:

-ов , он - толщина обшивки верхней и нижней панелей соответственно;

-nСТР.В , nСТР.Н - число стрингеров верхней и нижней панелей соответственно;

-fСТР.В , fСТР.Н - площади стрингеров верхней и нижней панелей соответственно;

переднего нижнего и заднего нижнего лонжеронов соответственно.

29

Крутящий момент в тонкостенном однозамкнутом контуре создает касательные напряжения, обратно пропорциональные толщине стенок контура:

1. Напряжение от крутящего момента, действующее на верхнюю часть обшивки:

350084,24 К.О.В. = 2×2,07×0,0035 = 24,16[МПа];

2.Напряжение от крутящего момента, действующее на нижнюю часть обшивки:

350 084,24 К.О.Н. = 2×2,07×0,003 = 28,19[МПа];

3. Напряжение от крутящего момента, действующее на стенку переднего лонжерона:

350084,24 К.ст.п. = 2×2,07×0,004 = 21,14[МПа];

4.Напряжение от крутящего момента, действующее на стенку заднего лонжерона:

350084,24 К.ст.з. = 2×2,07×0,0045 = 18,78[МПа];

Где:

- Fo - площадь, охватываемая контуром, равная:

30

= 3,56×0,5806 = 2,07 [ ];

-- толщина обшивки (верхней или нижней) или стенки лонжерона (переднего, заднего);

-МКР - максимальный крутящий момент, равный МКР = 350 054,84 [Нм];

Из формул видно, что жесткость (сопротивляемость) крыла на кручение весьма существенно зависит от площади замкнутого контура поперечного сечения F0 , потом - от толщины стенок контура .

Поперечная сила Q вызывает наибольшие касательные напряжения Q в нейтральном слое балки, а у верхнего и нижнего слоя балки Q = 0 (где в крыле расположены обшивка, полки лонжеронов и стрингеры). Можно приближенно считать, что поперечную силу воспринимают две вертикальные стенки лонжеронов, причем передняя воспринимает 70% поперечной силы сечения,

а задняя - 30% *Q сеч , поэтому:

Найдем напряжения, действующие от максимальной перерезывающей силы.

1. Напряжение от поперечной силы, действующее на стенку переднего лонжерона:

Где:

-Qсеч - величина максимальной поперечной силы;

-СТ.П и СТ.З - толщина стенки лонжерона (переднего или заднего).