Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
Раздел 2. МЕТОДЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ И ПОМЕХ
Лекции 2/1 – 2/2. Представление сигналов и помех рядами и преобразованиями Фурье
2015
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
Сигналы и помехи в РЭС ГА могут быть случайными и детерминированными, периодическими и непериодическими, дискретными и непрерывными.
В зависимости от вида решаемых задач может возникать необходимость
определения амплитудно-частотных или фазовых характеристик сигналов и помех, их корреляционных свойств, энергетических зависимостей или других каких-либо характеристик.
Поэтому для представления сигналов и помех применяют различные математические модели.
Особое место среди математических моделей сигналов и помех, с инженерной точки зрения, занимает представление сигналов и помех рядами и преобразованиями Фурье.
Представление сигналов и помех рядами и преобразованиями Фурье применяется при необходимости проведения спектрального анализа детерминированных сигналов и помех.
Теория спектральных преобразований разрабатывается уже несколько веков, но широкое практическое применение она получила с развитием электросвязи и разработкой измерительной аппаратуры, позволяющей определять временные и спектральные характеристики сигналов и помех.
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
Существующая измерительная аппаратура (осциллографы, анализаторы
спектра, селективные вольтметры, аппаратурно-программные измерительные комплексы) позволяет специалисту оценивать качество канала передачи (извлечения) информации, качество работы аппаратуры РЭС, ее исправность, проводить диагностирование и поиск неисправностей в аппаратуре.
В настоящее время с развитием и совершенствованием микропроцессорной техники, цифровых методов формирования, передачи и обработки сигналов еще шире
используется накопленный потенциал теории спектрального анализа.
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
1. Представление сигналов и помех рядами Фурье
Пусть сигнал или помеха являются детерминированным периодическим процессом
и описываются функцией s(t).
Любую детерминированную неслучайную периодическую функцию s(t) с
периодом T, удовлетворяющую условиям Дирихле, можно разложить в ряд по базисным функциям ψk(t), называемый рядом Фурье:
s(t) ck k (t),
k 0
где ψk(t) – k-я функция разложения из базиса {ψk(t)}, k = [0, ];
ck – k-й коэффициент разложения в ряд Фурье, получающийся в результате скалярного произведения функции s(t) и k-й базисной функции ψk(t), т.е.
|
|
|
T |
|
1 |
|
2 |
ck |
|
|
T |
T |
|
||
|
|
s(t) k (t)dt. |
|
|
|
|
2 |
|
|
|
|
|
|
Кафедра «Радиоэлектронных систем» |
|
|
|
Дисциплина ОТРЭС |
|
|
T |
|
|
|
|
2 |
При этом, если |
|
s(t) k (t)dt 0при n ≠ k, то базис {ψk(t)} ортогональный, а если, |
|
|
T |
|
T |
|
2 |
||
|
2 |
|
|
кроме того, |
s(t) k (t)dt 1 при n = k, то базис {ψk(t)} ортонормированный. |
||
|
T |
|
|
|
2 |
|
|
При представлении электрических сигналов рядом Фурье очень часто в качестве базисных функций ψk(t) применяют гармонические функции.
Базис гармонических функций {cos(2πfkt + φk)} называется тригонометрическим базисом. Тригонометрический базис ортонормированный.
Частоты колебаний гармонических функций тригонометрического базиса определяются соотношением
fk = kf1 = k/T,
где k = 0, 1, 2... .
Частота fk при k = 1, равная f1=1/T, называется основной частотой, а соответствующее ей
гармоническое колебание называется первой гармоникой разложения сигнала s(t) в ряд Фурье.
Гармонические колебания, имеющие значения частот, кратные основной частоте: kf1 при k > 1, называются гармониками основной частоты f .
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
Представление сигнала s(t) рядом Фурье в базисе тригонометрических функций
позволяет перейти от анализа этой функции во временной области к ее анализу в частотной области, т.е. к спектральному анализу:
s(t) Ak cos(2 kf1t k ), где Ak – амплитуда k-й гармоники;k 0
φk – начальная фаза k-й гармоники.
При спектральном анализе каждую гармонику удобно представлять в виде суммы двух ортогональных гармонических колебаний с нулевыми начальными фазами (так называемых квадратурных составляющих гармоники) и амплитудами ak и bk:
Akcos(2πkf1t + φk ) = akcos2πkf1t + bksin2πkf1t.
Такое представление позволяет перейти от базиса ортогональных функций, имеющих различные начальные фазы φk, к расширенному в два раза базису ортогональных
функций {cos2πkf1t, sin2πkf1t}, имеющих нулевые начальные фазы.
В этом случае амплитуда и начальная фаза k-й гармоники разложения в ряд Фурье сигнала s(t) определяются соотношениями:
|
|
|
|
|
|
arctg |
bk |
. |
|
A |
a2 |
b2 |
; |
|
k |
||||
|
|||||||||
k |
k |
k |
|
|
|
ak |
|||
|
|
|
|
|
|
|
|||
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
Амплитуды квадратурных составляющих k-й гармоники ak
коэффициентами Фурье и |
определяются следующим образом: |
|||||||||||||||
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
T |
||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
2 |
a |
k |
|
|
|
|
s(t) cos 2 kf tdt; |
b |
|
|
|
s(t)sin 2 kf tdt для k |
|||||
|
|
|
|
|
||||||||||||
|
|
T |
T |
|
|
|
|
1 |
k |
|
T |
1 |
||||
|
|
|
|
|
|
|
T |
|
|
T |
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
a |
0 |
|
|
|
s(t)dt; |
b 0. |
|
|||
|
|
|
|
|
|
|
|
|
||||||||
При k = 0 получим: |
|
|
T |
T |
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и bk называются
1, 2, ....
Множество коэффициентов Фурье {ak} и {bk} , k = [1, ∞], образуют спектр Фурье
периодического сигнала s(t).
С учетом изложенного, сигнал s(t) можно представить в виде: |
|||||
s(t) a0 |
(a |
k |
cos 2 kf t b |
sin 2 kf t). |
|
2 |
k 1 |
1 |
k |
1 |
|
|
|
|
|
||
Слагаемое a0/2 называется постоянной составляющей спектра амплитуд сигнала s(t) (т.к. f0 = 0 при k = 0), или средним значением сигнала s(t) на периоде T.
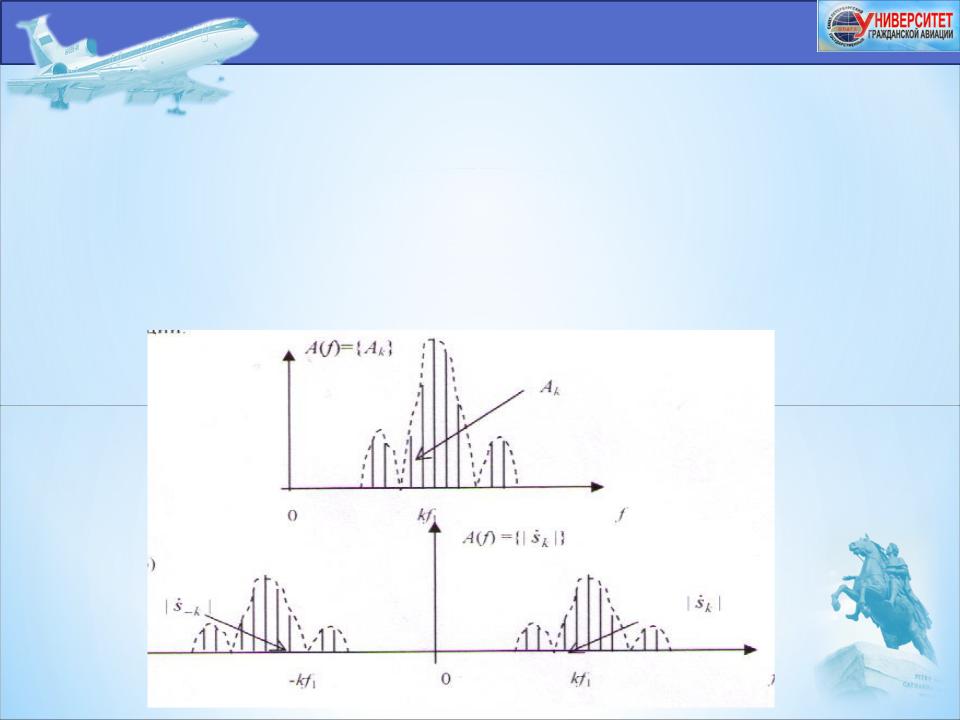
Множества {Ak} и {φk}, где k = [1, ∞], образуют спектр амплитуд A(f) и спектр фаз φ(f) периодического сигнала s(t).
Спектр периодического сигнала s(t) дискретный (или линейчатый), так как частоты гармонических составляющих спектра кратны основной (первой) гармонике.
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
В некоторых случаях для решения задач анализа или синтеза сигналов и помех или радиотехнических цепей и устройств удобнее представлять периодический сигнал
или помеху s(t) в виде разложения в ряд Фурье в базисе экспоненциальных функций {exp(j2πkf1t)}:
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
|
|
s(t) sk |
e j 2 kf1t , |
|
|||||||
где f1 = 1/T. |
|
|
|
|
|
|
|
k |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комплексные коэффициенты разложения |
|
sk |
и bk |
||||||||||||
|
связаны с коэффициентами Фурье ak |
||||||||||||||
соотношением |
. |
1 |
(a |
|
|
jb ) |
1 |
|
. |
|
|
, |
где k [ , ] и k 0, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||
|
sk |
2 |
|
2 |
|
|
sk |
|
e k |
|
|||||
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
||
|
s. |
|
|
|
где |
k a2 |
b2 |
||
|
|
k |
k |
|
|
|
|
||
k arctg bk ak
При k = 0 получаем
–k-я составляющая спектра амплитуд сигнала s(t);
–k-я составляющая спектра фаз сигнала s(t).
постоянную составляющую сигнала s(t): |
|||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
. |
|
1 |
|
2 |
a0 |
||
|
|
|
|||||||
|
|
s0 |
|
|
T s(t)dt |
||||
|
|
|
|
|
|
|
|
||
|
|
|
T |
|
2 |
|
|||
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
Спектральное представление периодических сигналов в базисе экспоненциальных функций содержит положительные и отрицательные частоты.
Отрицательные частоты в природе не существуют. Они появляются как следствие формального представления гармонических колебаний в базисе экспоненциальных комплексных функций.
Используя формулы Эйлера: ejx = cosx + jsinx; e-jx = cosx – jsinx,
нетрудно показать, что при переходе от экспоненциальной формы представления к тригонометрической понятие отрицательная частота теряет смысл.
Кафедра «Радиоэлектронных систем»
Дисциплина ОТРЭС
Аппарат рядов Фурье может быть использован для финитных детерминированных сигналов или помех, существующих на интервале [0,T] (в предположении, что за пределами данного интервала сигнал или помеха повторяются).
2.2. Представление сигналов и помех преобразованиями Фурье
Пусть детерминированный непериодический сигнал s(t), заданный на оси t от - до + , удовлетворяет условиям Дирихле и условию абсолютной интегрируемости, тогда для такого сигнала могут быть определены прямое и обратное преобразования Фурье:
Функция частоты Ф(j2πf)
сигнала s(t).
Ф( j2 f ) s(t)e j 2 ft dt;
называется комплекснойj 2 ft спектральной плотностью (КСП) s(t) Ф( j2 f )e df
Произведение Ф(j2πf)df имеет смысл коэффициентов ряда Фурье, следующих через бесконечно малые интервалы частот df и описывающих сигнал s(t) с бесконечно большим периодом, то есть с T → ∞.