
Физика. Краткая теория и примеры решения задач. Методическое пособие 2016
..pdf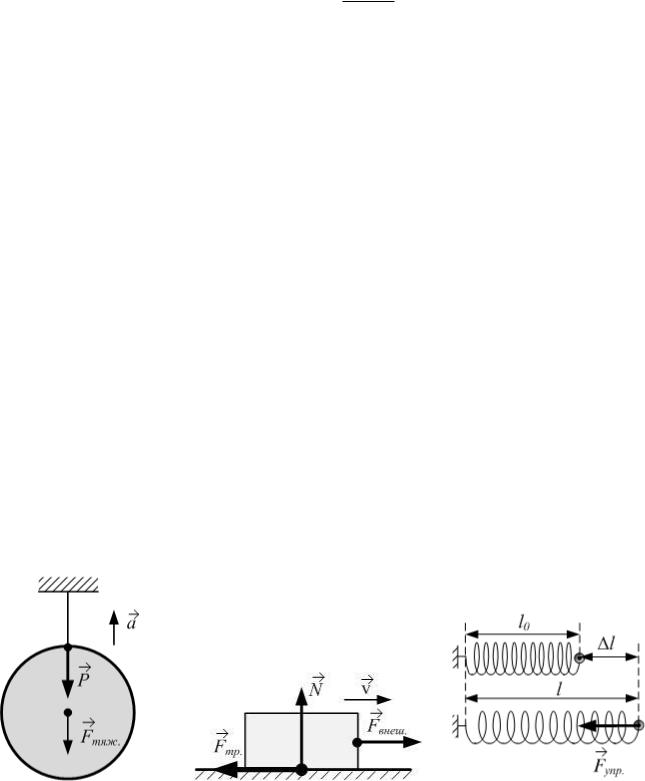
Fтяг. m1r2m2 ,
где – гравитационная постоянная; m1 и m2 – массы взаимодействующих тел, рассматриваемые как материальные точки; r – расстояние между ними.
Сила тяжести
|
|
|
F |
mg |
M m |
, |
|
|
|
R h 2 |
|||
|
|
|
тяж. |
|
|
|
|
|
|
|
|
|
|
где |
g |
M |
– ускорение свободного падения, M – масса Земли, R – |
|||
|
||||||
R h 2 |
||||||
радиус Земли, h – высота тела массой m над Землёй.
Вес тела – сила, приложенная к подставке или подвесу (рис. 1.8). Вес
|
|
|
|
тела, движущегося с ускорением a , равен |
|
|
|
|
|
, |
|
P mg |
ma |
||
где m – масса тела. Если ускорение тела направлено вертикально вверх, то вес P m(g a) ; а если вертикально вниз, то P m(g a) .
Сила трения скольжения (рис. 1.9):
Fтр. N ,
где – коэффициент трения, N – сила нормального давления.
Сила трения покоя:
0 Fтр.покоя N .
Сила упругости (закон Гука):
Fупр. k l ,
где k – коэффициент упругости (жесткость пружины), l l l0 – абсолютная деформация (рис. 1.10).
Рис. 1.8 |
Рис. 1.9 |
Рис. 1.10 |
|
||
|
|
Радиус-вектор rc и координаты центра масс системы материальных точек:
11

|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mi |
ri |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
i 1 |
|
|
|
; |
|
|
|
|
|
|
|
||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
N |
mi xi |
|
|
|
N |
yi |
|
|
|
N |
mi zi |
|
||||||
|
|
|
|
|
mi |
|
|
|
|
|
|||||||||
x |
i 1 |
|
|
, |
y |
i 1 |
|
|
, |
z |
c |
|
i 1 |
|
|
, |
|||
|
N |
|
|
|
|
N |
|||||||||||||
c |
|
c |
|
|
N |
|
|
|
|
|
|
|
|
||||||
|
|
mi |
|
|
|
|
mi |
|
|
|
|
|
|
|
mi |
|
|||
|
i 1 |
|
|
|
|
i 1 |
|
|
xi |
|
|
|
i 1 |
|
|||||
где mi – масса i-той материальной точки; ri |
, |
, yi , zi – её радиус-вектор и |
|||||||||||||||||
N
координаты; mi – масса всей системы; N число точек.
i1
Плотность тела:
|
|
|
|
|
|
|
m |
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
V |
|
|
|
||
|
Уравнение движения центра масс: |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
|
|
Fkвнеш. |
||||||
|
|
|
|
r |
|
k |
|
|
|
|||||
|
|
a |
|
|
|
c |
|
|
|
, |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
c |
|
dt |
2 |
|
|
|
mi |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
где |
|
|
|
|
|
|
|
|
|
– |
сумма всех внешних сил, |
|||
a |
– ускорение центра масс; F |
внеш. |
||||||||||||
|
c |
|
|
|
|
|
k |
|
|
|
||||
k
приложенных к системе.
Закон сохранения импульса: если сумма внешних сил равна нулю, то полный импульс системы сохраняется.
|
N |
|
внеш . 0 |
|
|
Если F |
, |
||
|
i 1 |
i |
|
|
|
|
|
|
|
N |
|
|
N |
|
или m i const , или |
|
piнач. |
|
|
i 1 |
|
|
i 1 |
|
N
то pi const ,
i 1
N
i 1
piкон. .
где N – число материальных точек (или тел), входящих в систему. |
|||||||
|
|
|
|
|
|
||
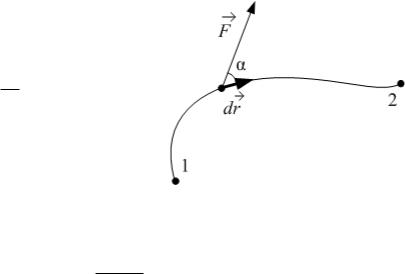
Работа, совершаемая постоянной силой F : |
|
||||||
|
|
, или A F |
|
|
|
|
cos , |
|
|
||||||
A F |
r |
|
r |
|
|
||
|
– перемещение, – угол между направлениями векторов силы F и |
||||
где r |
|||||
перемещения r (рис. 1.11): |
|
|
|
||
|
|
|
|
|
|
Работа, совершаемая переменной силой F : |
|
||||
|
2 |
2 |
|
2 |
|
|
A12 dA F |
dr |
F r cos dr , |
|
|
|
1 |
1 |
|
1 |
|
где интегрирование |
производится |
вдоль траектории (рис. |
Рис. 1.11 |
||
1.12). |
|
|
|
|
|
12
Средняя мощность за интервал времени t :
 P
P At .
At .
Мгновенная мощность:
|
dA |
|
|
|
|
P |
|
, или |
P F |
F cos , |
|
dt |
Рис. 1.12 |
где dA – работа, совершаемая за промежуток
времени dt , – скорость тела, – угол между скоростью и силой.
Коэффициент полезного действия
Aполез. .
Aзатр.
Закон изменения полной энергии для незамкнутой системы:
W Aвнешн .сил , или |
Wполн.1=Wполн.2+Асистемы против внешних сил |
Закон изменения механической энергии для незамкнутой системы:
Wмех.1=Wмех.2+Асистемы против внешних сил+Асистемы против диссипативных сил
Кинетическая энергия материальной точки (или тела), движущейся поступательно:
W |
m 2 |
, или W |
p2 |
|
|
|
. |
||
|
|
|||
k |
2 |
k |
2m |
|
|
|
|||
Потенциальная Wp энергия тела и консервативная сила,
действующая на тело в данной точке поля, связаны соотношением:
|
grad W |
|
, |
|
|
|
|
W |
p |
|
|
W |
p |
|
|
W |
p |
|
F |
|
или F |
i |
|
|
j |
|
|
k |
|
|
. |
||||||
p |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
x |
|
y |
|
|
|
z |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В проекциях: |
F |
Wp |
, |
F |
Wp |
, |
F |
Wp |
. |
||||
|
|
|
|
|
x |
x |
|
y |
y |
z |
z |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь |
i |
, |
j |
и k – единичные векторы (орты). В частном случае, когда |
|||||||||
поле сил обладает сферической симметрией (как, например, гравитационное),
|
F |
dWp |
. |
|
|
|
|
|
|
||
|
r |
dr |
|
|
|
|
|
|
|
||
Закон сохранения полной энергии: |
|
|
|
|
|
|
внеш. 0 , |
|
|
W |
|
Если F |
то W |
. |
|||
i |
|
|
полн.1 |
полн.2 |
|
i
Здесь Wполн.1 и Wполн.2 – полная энергия системы; сумма всех видов энергии для начального и конечного состояния системы соответственно.
Закон сохранения механической энергии (выполняется в замкнутой системе, в которой действуют только консервативные силы):
внеш.
Если Fi 0 и отсутствуют диссипативные силы, то Wмех.1=Wмех.2 .
i
13

Здесь Wмех.1 и Wмех.2 – полная механическая энергия системы; сумма всех
видов потенциальной и кинетической энергии для начального и конечного состояния системы соответственно (Wмех. Wk Wp ).
Потенциальная энергия упруго деформированного тела (сжатой или растянутой пружины)
Wp k l 2 , 2
где k – жёсткость пружины, l – абсолютная деформация.
Потенциальная энергия гравитационного взаимодействия
Wp m1 m2 , r
где r – расстояние между двумя точечными массами m1, и m2, – гравитационная постоянная.
Потенциальная энергия тела в однородном поле силы тяжести:
Wp m g h ,
где h – высота тела над уровнем, принятым за нулевой, g – ускорение свободного падения. Эта формула справедлива при условии h R , где R – радиус Земли.
Динамика вращательного движения
Момент силы F , действующей на тело, относительно оси вращения (рис. 1.13):
M F l ,
Рис. 1.13
где F – проекция силы F на плоскость, перпендикулярную оси вращения; l –
плечо силы F (кратчайшее расстояние от оси вращения до линии действия силы).
14
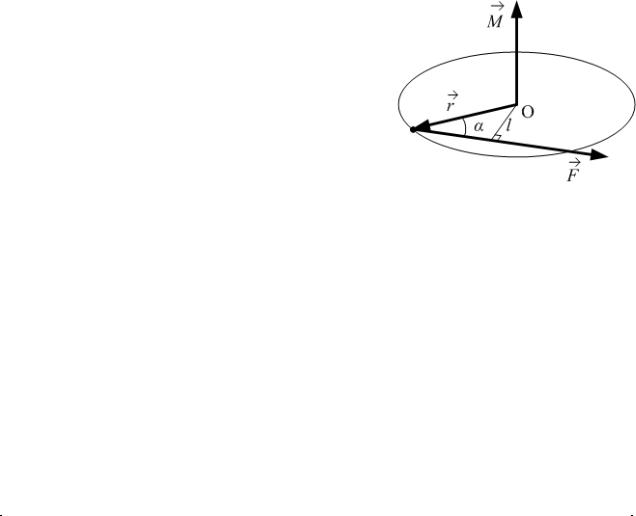
Момент силы относительно точки: |
|
|
|
||||
|
|
|
|
|
|
|
|
|
M [r |
F], |
|
|
|
||
|
M F r sin , |
|
|
|
|||
– радиус-вектор точки приложения силы, |
(рис. |
||||||
где r |
– угол между r |
и F |
|||||
1.14).
Момент инерции материальной точки относительно оси вращения:
J мат.точки m r2 ,
где т – масса точки; r – расстояние от точки до оси вращения;
Момент инерции системы материальных точек относительно оси вращения (или твёрдого тела, которое можно представить как систему дискретных материальных точек):
|
|
N |
m |
|
, |
J |
сист.точек |
|
r2 |
||
|
i 1 |
i |
i |
|
|
|
|
|
|
|
где mi – масса i-той точки; ri – её расстояние до оси вращения, N – число точек в системе.
Момент инерции твёрдого тела с
непрерывно распределённой массой:
J r2dm .
m |
Рис. 1.14 |
Если тело однородно, то есть его плотность одинакова по всему объёму, то dm dV , и
J r2dV ,
V
где V – объём тела.
Таблица 1
Моменты инерции некоторых тел правильной геометрической формы
Тело |
Ось, относительно которой |
Формула |
|||
определяется момент инерции |
момента инерции J |
||||
|
|||||
|
|
|
|
||
|
Проходит через центр тяжести |
|
m l 2 |
||
|
стержня перпендикулярно |
|
|
|
|
|
12 |
|
|||
Однородный тонкий |
стержню |
|
|||
Проходит через конец |
|
|
|
||
стержень массой т и длиной l |
|
m l 2 |
|
||
стержня перпендикулярно |
|
||||
|
|
||||
|
стержню |
3 |
|
||
|
|
|
|||
|
|
|
|
|
|
Тонкое кольцо, обруч, |
Проходит через центр |
|
|
|
|
труба радиусом R и массой т, |
|
|
|
||
перпендикулярно плоскости |
m R2 |
||||
маховик радиусом R и массой |
|||||
основания |
|
|
|
||
т, распределённой по ободу |
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
15

Круглый однородный диск |
Проходит через центр диска |
|
|
|
m R2 |
|
||||||
(цилиндр) радиусом R и |
перпендикулярно плоскости |
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|||||||||
массой т |
|
основания |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Толстостенная |
трубка, |
|
|
|
|
|
|
|
|
|
|
|
круглый однородный |
полый |
Проходит через центр диска |
|
m |
|
R1 |
R2 |
|
||||
|
|
|
|
|
|
|
|
|||||
диск (цилиндр) массой т с |
перпендикулярно плоскости |
|
2 |
2 |
|
|||||||
2 |
|
|
||||||||||
внутренним радиусом R1 и |
основания |
|
|
|
|
|
|
|
|
|
||
внешним радиусом R2 |
|
|
|
|
|
|
|
|
|
|
|
|
Однородный шар массой т |
Проходит через центр шара |
|
|
2 |
m R2 |
|
||||||
и радиусом R |
|
5 |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
||||||||||
Теорема Штейнера: момент инерции тела относительно произвольной |
||||||||||||
оси равен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J J |
c |
m d 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Jc – момент инерции этого тела относительно оси, проходящей через
центр масс тела параллельно заданной оси; d – расстояние между осями; m – масса тела (рис. 1.15).
Момент импульса вращающегося тела относительно оси: |
|||
|
|
|
|
L J , |
|
– его угловая |
|
где J – момент инерции |
тела, |
|
|
скорость.
Закон сохранения момента импульса. Если суммарный момент внешних сил, действующих на систему, равен нулю, то полный момент импульса системы сохраняется:
Если M
i
или
внеш. 0, i
N
Liнач.
i1
|
N |
|
то |
Li const , |
|
|
i 1 |
Рис. 1.15 |
|
||
N |
|
|
Liкон. , i 1
где Li – момент импульса i-го тела, входящего в состав системы, N – число тел в системе. Для двух взаимодействующих тел замкнутой системы:
|
|
|
|
|
|
|
|
|
|
|
|
J1 1 J2 2 J1 1 J2 |
2 |
|
|||
где J1 , J2 , 1 |
и |
2 |
– |
моменты инерции |
и |
угловые |
скорости тел до |
|
взаимодействия: |
|
|
|
|
|
|
|
|
J1 , J2 |
, 1 |
и 2 – те же величины после взаимодействия. |
||||||
Закон сохранения момента импульса для одного тела, момент |
||||||||
инерции которого меняется: |
|
|
|
|
||||
|
|
|
|
J1 1 J2 2 , |
|
|
|
|
где J1 и J2 – начальный и конечный моменты инерции; 1 |
и 2 – начальная |
|||||||
и конечная угловые скорости тела.
16
Основное уравнение динамики вращательного движения твердого
тела |
относительно |
неподвижной оси |
(второй |
закон Ньютона для |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
вращательного движения): угловое ускорение тела прямо пропорционально |
||||||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
суммарному моменту |
Mi |
внешних |
сил |
и |
обратно пропорционально |
|||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
моменту инерции J тела: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
Mi |
|
|
|
||
|
|
|
|
|
|
i 1 |
|
|
|
|
||
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
J |
|
|
|
|
Второй закон Ньютона для вращательного движения в импульсной |
||||||||||||
форме |
(закон |
изменения момента |
импульса |
тела): изменение момента |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
импульса тела |
dL равно импульсу M dt суммарного момента M внешних |
|||||||||||
сил: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt . |
||||
|
|
|
dL |
M dt , |
или |
d J |
M |
|||||
Если момент сил, действующих на тело, постоянен, то |
||||||||||||
|
|
|
|
|
|
или |
|
|
|
|
t , |
|
|
|
|
L |
M t , |
J M |
|||||||
где t |
(или dt ) – промежуток времени, в течение которого действовал момент |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
сил M |
; J – момент инерции тела, – его угловая скорость. |
|||||||||||
Работа момента силы M при вращательном движении: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
dA M d , |
|
|
A dA M d . |
||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
Если момент сил постоянен ( M const ), то работа равна
A M .
Здесь (или d ) – угол поворота.
Мгновенная мощность, развиваемая при вращении тела:
PM .
Кинетическая энергия вращающегося тела:
|
|
|
|
|
|
|
|
|
W |
J 2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Кинетическая энергия тела, катящегося по плоскости без |
||||||||||||||||
скольжения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
W W |
W |
|
|
m 2 |
|
J 2 |
|||||
|
|
|
|
|
|
|
|
|
c |
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
k |
k.пост. |
k.вращ |
|
|
2 |
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
m 2 |
|
|
|
|
|
|
|
|
|
|
|
||
где W |
|
|
c |
– кинетическая энергия поступательного движения тела; |
||||||||||||||
|
|
|
||||||||||||||||
|
|
k.пост. |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
скорость |
центра масс |
тела; W |
|
|
|
J 2 |
– |
кинетическая энергия |
|||||||
c |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
k.вращ |
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вращательного движения тела вокруг оси, проходящей через центр масс.
17

Механические колебания
Кинематическое уравнение гармонических колебаний x Acos t 0 ,
Здесь х – смещение колеблющейся точки из положения равновесия; t – время;
А – амплитуда колебаний; ω – круговая (циклическая) частота колебаний;
0 – начальная фаза колебаний;
t 0 – фаза колебаний в момент t.
Круговая (циклическая) частота колебаний:
2 , или |
|
2 |
, |
|
T |
||||
|
|
|
где и Т – частота (линейная частота) и период колебаний соответственно.
Скорость точки, совершающей гармонические колебания:
dxdt A sin t 0 .
Ускорение колеблющейся точки при гармонических колебаниях:
a d 2 A cos t 0 . dt
Период колебаний пружинного маятника (тела массой m,
подвешенного на пружине жёсткостью k, рис. 1.16):
Tпруж. 2 
 mk .
mk .
Формула справедлива для малых колебаний, пока выполняется закон Гука F k x , и в пренебрежении массой пружины в сравнении с массой тела.
Период колебаний математического маятника (материальной точки массой m, подвешенной на нерастяжимой невесомой нити длиной l, рис. 1.17):
Tмат. 2 
 gl ,
gl ,
где g – ускорение свободного падения.
Период колебаний физического маятника (твёрдого тела,
подвешенного в поле силы тяжести и способного колебаться относительно оси, не проходящей через центр масс, рис. 1.18):
T |
2 |
|
lпр. |
|
2 |
|
J |
|
. |
|
|
||||||||
физ. |
|
|
g |
mgl |
|||||
|
|
|
|||||||
Здесь J – момент инерции колеблющегося тела относительно оси колебаний, l – расстояние от центра масс маятника до оси (длина физического
маятника), lпр. |
J |
– приведённая длина физического маятника (то есть |
|
|
|||
m l |
|||
|
|
18

Рис. 1.16 |
Рис. 1.17 |
|
Рис. 1.19 |
|
Рис. 1.18 |
||
|
|
||
|
|
|
длина такого математического маятника, который имеет тот же период колебаний).
Формулы для периода колебаний физического и математического маятников справедливы при малых углах отклонения, когда можно положить sin . Для α=150 ошибка в значении периода не превышает 1 %, а при α=30 ошибка равна 0.005 %.
Период колебаний крутильного маятника (тела, подвешенного на упругой нити, рис. 1.19):
T |
2 |
|
J |
|
, |
|
|||||
кр. |
|
|
kкр. |
||
|
|
|
|||
где J – момент инерции тела относительно оси, совпадающей с нитью, kкр. –
модуль кручения нити. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука: M kкр. . Здесь M – момент
упругой силы, возникающей при закручивании нити на угол .
Полная энергия гармонического осциллятора:
kA2 m 2 A2
Wполн. 2 2
Закон сохранения энергии при гармонических колебаниях:
|
W |
W |
|
W |
|
|
m 2 |
|
kx2 |
|
kA2 |
const . |
|
|
|
p |
|
|
|
|
|||||||
|
полн. |
k |
|
2 |
2 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||||
Амплитуда |
|
|
А |
|
|
результирующего |
колебания |
||||||
x x1 x2 |
Acos t 0 , |
полученного |
при |
сложении двух |
колебаний |
||||||||
одинаковой частоты, происходящих по одной прямой, x1 A1 cos t 1 и
x2 A2 cos t 2 ,
равна
A 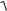
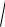 A12 A22 2A1 A2 cos( 2 1) ,
A12 A22 2A1 A2 cos( 2 1) ,
19
где А1 и А2 – амплитуды исходных колебаний; 1 и 2 – их начальные
фазы (см. сложение колебаний по методу векторных диаграмм на рис.
1.20).
Начальная фаза
результирующего колебания при сложении однонаправленных колебаний:
0 arctg A1 sin 01 A2 sin 02 . A1 cos 01 A2 cos 02
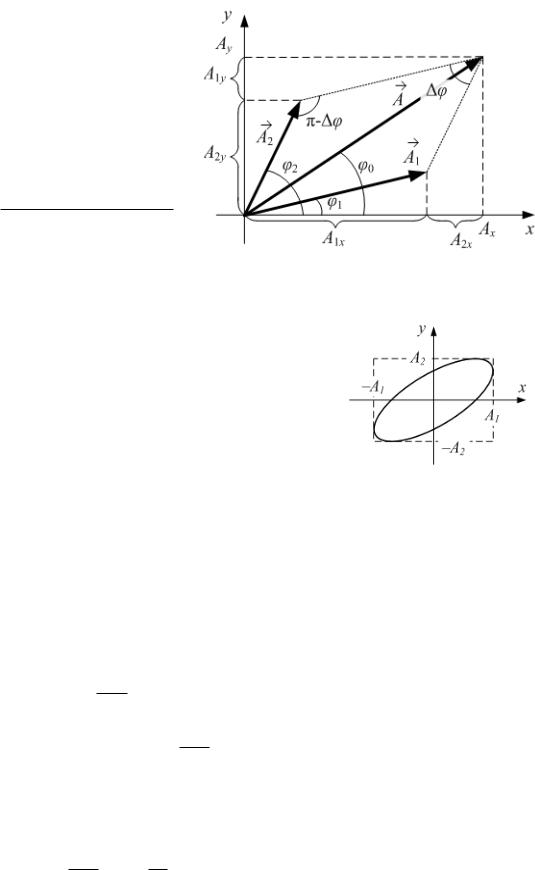
Уравнение траектории (рис.
1.21) точки, участвующей в двух Рис. 1.20
взаимно перпендикулярных
колебаниях одинаковой частоты,
x A1 cos t 1 и y A2 cos t 2 ,
самплитудами А1 и А2 и начальными фазами 1 и
2 :
|
x2 |
|
y2 |
2 |
xy |
cos( ) sin 2 ( ) , |
|
|
|
|
|
|
|
||||
|
A12 |
|
A22 |
A1A2 |
|
|
||
где 2 1 – сдвиг фаз колебаний. |
Рис. 1.21 |
|||||||
Возвращающая |
(квазиупругая) сила, |
|||||||
|
||||||||
действующая на тело массой m при гармонических колебаниях:
F 2 m x k x ,
где х – смещение колеблющейся точки из положения равновесия; ω –
циклическая частота колебаний; – коэффициент пропорциональности. В частном случае пружинного маятника он равен жёсткости пружины.
Дифференциальное уравнение гармонических колебаний
m d 2 x k x , или в стандартной форме: dt 2
d 2 x 2 x 0 , dt 2
где x – колеблющаяся величина; ω – круговая (циклическая) частота колебаний; k m 2 – коэффициент квазиупругой силы.
Дифференциальное уравнение затухающих колебаний
m d 2 x r dx k x , или в стандартной форме: dt2 dt
20
