Физика. Краткая теория и примеры решения задач. Методическое пособие 2016

Здесь p – давление газа; E – средняя энергия поступательного движения молекул; n – концентрация молекул; k – постоянная Больцмана.

Теорема о равнораспределении энергии по степеням свободы. На любую степень свободы приходится в среднем одинаковая энергия, равная

E1 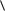k T . 2

Число i степеней свободы молекул газа:

-для одноатомных газов i=3;

-для двухатомных газов i=5;

-для многоатомных газов i=6.

Из них число поступательных степеней свободы: iпост. 3 для любых молекул; число вращательных степеней свободы: iвр. 2 для двухатомных газов и iвр. 3 для многоатомных газов.

Средняя кинетическая энергия молекулы идеального газа:

E 2i kT .

Внутренняя энергия произвольной массы идеального газа:

U 2i RT .

Суммарная кинетическая энергия поступательного движения

молекул газа:

Uпост. 23 RT .

Средняя энергия вращательного движения молекулы:

E вр. iвр2. kT .

Суммарная кинетическая энергия вращательного движения молекул

газа:

Uвр. iвр2. RT .

Здесь m – количество вещества; m – масса газа; – молярная масса;

R – универсальная газовая постоянная; k – постоянная Больцмана, i – число степеней свободы молекул; iвр. – число вращательных степеней свободы; T –

абсолютная температура.

Понятие о классической статистике

Вероятность того, что случайная величина x примет значение xi :

101

wi lim Ni ,

N N

где N – полное число измерений, Ni – число опытов, в которых величина x принимает значение xi .

Условие нормировки. Сумма вероятностей по всем возможностям есть

достоверное событие, вероятность которого равна единице:

wi 1.

i

Среднее арифметическое значение случайной величины x:

где xi – значение величины x в i-том измерении; N – число измерений; wi – вероятность того, что величина x принимает значение xi .

Среднее квадратичное случайной величины x:

Вероятность dw того, что случайная величина принимает значения

винтервале от x до x+dx ( x x; x dx ), прямо пропорциональна величине

интервала dx:

dw f x dx ,

где коэффициент пропорциональности f(x), зависящий от x, это – функция распределения вероятностей случайной величины x.

Вероятность dw того, что молекула идеального газа имеет скорость в промежутке от до d ( ; d ), равна отношению числа dN молекул, обладающих скоростями в заданном промежутке, к полному числу молекул N:

dw dNN .

Число dN молекул идеального газа, имеющих скорости в промежутке от до d ( ; d ), пропорционально полному числу молекул N и величине интервала скоростей d :

dN f ( ) N d ,

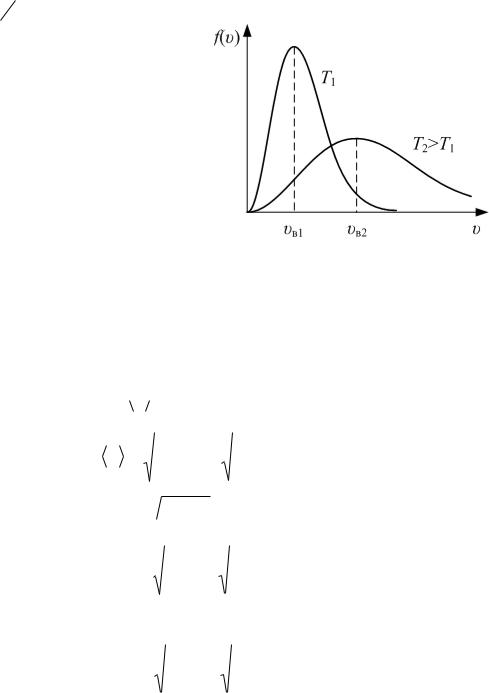
где f – функция распределения Максвелла (см. рис.6.1), равная

102

Доля молекул идеального газа, имеющих скорости в промежутке от

до d ( ; d ), равна N .

N

Характерные скорости молекул газа:

- средняя арифметическая: 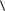f d , или

0

- средняя квадратичная: кв. 2 , где 2 2 f d , или

0

- наиболее вероятная (соответствует максимуму функции распределения Максвелла, см. рис. 6.1):

Здесь n – концентрации частиц в произвольной точке силового поля; Eпот. – их потенциальная энергия в данной точке; n0 – концентрации частиц в

точке, где потенциальная энергия равна нулю; k – постоянная Больцмана; T –

103

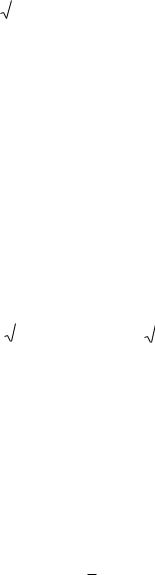
абсолютная температура; n1 и n2 – концентрации частиц в двух точках потенциального поля; E=E2–E1 – разность их потенциальных энергий в этих точках.

Барометрическая формула – закон уменьшения давления p идеального газа с высотой h в однородном потенциальном поле при постоянной температуре:

Здесь μ – молярная масса газа, p0 –давление при h=0, T – абсолютная температура, m0 – масса молекулы, R – универсальная газовая постоянная.

Явления переноса

Среднее число столкновений молекулы с другими молекулами в единицу времени:

средняя арифметическая скорость молекул; l – средняя длина свободного пробега.

Среднее время свободного пробега (средняя продолжительность свободного пробега):

Эффективное сечение молекулы

d 2 ,

где d – эффективный диаметр молекулы.

Средняя длина свободного пробега

где n – концентрация молекул; – эффективное сечение молекулы; d – эффективный диаметр молекулы.

Уравнение диффузии (закон Фика). Число частиц dN , перенесённых за время dt через малую площадку S , пропорционально градиенту

Здесь D – коэффициент диффузии, равный

D 13 l .

104

Масса вещества, перенесённого за время t через площадку S :

m D d S t , dz

где d – градиент плотности, D – коэффициент диффузии. dz

Закон Ньютона для вязкости. Сила вязкого трения, возникающая между слоями газа, движущимися параллельно, но с разными скоростями,

пропорциональна градиенту d скорости направленного движения слоёв в dz

направлении, перпендикулярном скорости (рис. 6.2):

молекул; l – средняя длина свободного пробега; D – коэффициент

105

удельная и молярная теплоемкости идеального газа при постоянном объёме; i

– число степеней свободы; – молярная масса газа, R – универсальная газовая постоянная.

Твёрдое тело: упругие свойства, тепловое расширение, классическая теория теплоемкости твёрдых тел

Относительная продольная деформация:

l , l

где l – абсолютное удлинение, l – длина тела.

Нормальное механическое напряжение – это сила, приходящаяся на единицу площади сечения:

FS .

Закон Гука:

жёсткость (коэффициент жёсткости), равный для стержня величине k ESl .

Закон Дюлонга и Пти. По классической теории теплоёмкостей, молярная изохорная теплоёмкость всех химически простых тел в твёрдом состоянии одинакова, не зависит от температуры и равна

CV=3R,

где R – универсальная газовая постоянная. Для химических соединений CV=3Rz, где z – число атомов в молекуле. При низких температурах закон несправедлив.

Зависимость длины твёрдого тела от температуры: l l0 1 t ,

где – температурный коэффициент линейного теплового расширения; t – температура в градусах Цельсия; l0 – длина тела при температуре t=00С.

Зависимость объёма твёрдого тела от температуры:

V V0 1 t ,

где – температурный коэффициент объёмного теплового расширения; t – температура в градусах Цельсия; V0 – объём тела при температуре t=00С. Для аморфных тел и для кристаллических тел с кубической решёткой 3 .

Число атомов, приходящихся на одну элементарную ячейку кристалла:

- для простой кубической решётки (рис. 6.3, а)

N 1;

- для гранецентрированной кубической решётки (рис. 6.3, б)

N 4 ;

106

- для объёмно-центрированной кубической решётки (рис. 6.3, в)

N 2 .

Рис. 6.3

Квантовые статистики. Энергия Ферми

Спин s – внутреннее характерное неотъемлемое свойство элементарных частиц (наряду с массой и зарядом). Спин электрона и фотона:

электрона, me – его масса. Спин – квантовый релятивистский эффект. Классического аналога для спина нет. Частицы подчиняются разным статистическим закономерностям, в зависимости от того, целый спин у частиц или полуцелый.

Функция распределения Бозе-Эйнштейна (квантовая статистика для бозонов – частиц с целым спином; пример - фотоны):

системы при добавлении в неё одной частицы при постоянных объёме и энтропии: V const и S const ).

107

Функция распределения Ферми-Дирака (квантовая статистика для фермионов – частиц с полуцелым спином; пример – электроны):

в i-том состоянии; – химический потенциал, в первом приближении для фермионов равный энергии Ферми ( EF ); k – постоянная Больцмана; T – температура. Для фермионов f (Ei ) имеет также смысл вероятности заполнения i-го состояния.

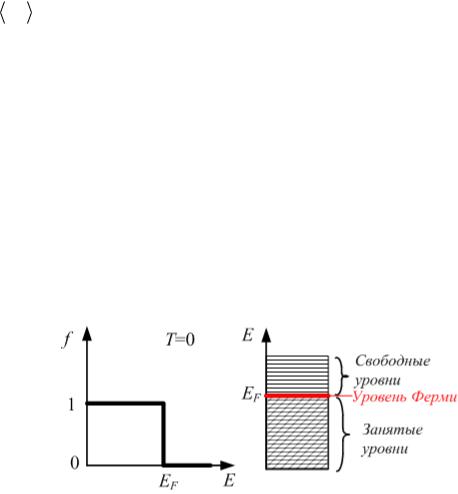
Энергия Ферми – это максимальная энергия электронов при T 0 ; она зависит от концентрации электронов n: чем больше частиц, тем большее число уровней будет занято и тем выше окажется последний занятый уровень (рис. 6.4), и тем выше соответствующая энергии EF температура Ферми TF :

равна 0.5:

Температурная зависимость сопротивления металлов и полупроводников. p-n – переход. Термоэлектричество

Зависимость сопротивления R и удельного сопротивления ρ

металла от температуры

Rме R0 1 t R0 T ,ме 0 1 t 0 T

108

где 2731 K 1 – температурный коэффициент сопротивления (удельного

сопротивления) для чистых металлов; R0 ( 0 ) – сопротивление (удельное

сопротивление) при t 00 C ., T – абсолютная температура.

Зависимость сопротивления R, удельного сопротивления ρ и

проводимости γ собственного полупроводника от температуры:

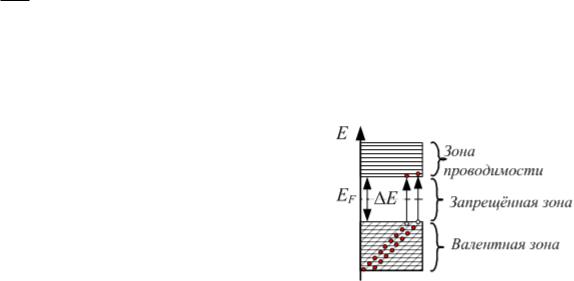
где k – постоянная Больцмана; T – абсолютная температура; E – ширина запрещённой зоны, то есть минимальная энергия, необходимая для

переходя электрона из валентной зоны в зону проводимости и образования пары электрон-дырка в беспримесном полупроводнике (рис. 6.5).

Сила тока, текущего через p-n – переход:

Здесь e – элементарный заряд, k – постоянная Больцмана, T – абсолютная температура, U – напряжение на p-n – переходе (U>0 для прямого включения

иU<0 – для обратного).

Термоэлектродвижущая сила (ТЭДС), возникающая в замкнутой

цепи, составленной из разнородных проводников с различными

температурами спаев (контактов):

T2 T1 ,

где (T2–T1) – разность температур спаев термопары; – удельная термо-ЭДС.

Ядерная физика

Дефект массы ядра:

m Z mp ( A Z ) mn mя , или m Z mH ( A Z ) mn ma ,

где mp – масса протона, mn – масса нейтрона, mH – масса атома водорода 11H , ma и mp – масса атома и его ядра ZA X , Z – зарядовое число ядра (число протонов в ядре), A – массовое число (суммарное число нуклонов – протонов

инейтронов – в ядре).

Энергия связи ядра

Eсв. m c2 ,

109

где m – дефект массы ядра, с – скорость света в вакууме. Если дефект массы

выражен в атомных единицах массы (а.е.м.), то c2 931.5 МэВ ; иначе говоря,

а.е.м.

1 а.е.м. эквивалентна энергии 931.5 МэВ.

Удельная энергия связи – это энергия связи, приходящаяся на один нуклон:

Eуд. EAсв. .

где А – массовое число.

Закон радиоактивного распада:

N N0 e t ,

где N0 – начальное число радиоактивных ядер в момент времени t=0; N –

число ядер, оставшихся нераспавшимися в момент времени t; λ – постоянная радиоактивного распада (вероятность распада ядра в единицу времени).

Период полураспада – это время, за которое распадается половина ядер; оно связано с постоянной радиоактивного распада:

ln 2

T12 .

Активность радиоактивного вещества – это число распадов в

единицу времени:

A dNdt , или A N ,

где λ – постоянная распада, N – число радиоактивных ядер в момент времени t.

Энергетический эффект ядерной реакции X a Y b :

E m c2 (система единиц СИ: [ m] кг , [ E] Дж), илиE 931.5 m (атомные единицы: [ m] а.е.м., [ E] МэВ ),

где mX , mY , mb и ma – массы ядер или частиц, участвующих в реакции;m mX ma mY mb – изменение массы при ядерной реакции.

Раздел 6. Задачи

401.В баллоне, объём которого 0,25 м3 находится газ, состоящий из смеси углекислого газа и паров воды. Температура газа 327 °С. Число молекул углекислого газа N1=6,6∙1021, число молекул паров воды N2=0,9∙1021. Вычислить давление р и среднюю молярную массу μ газовой смеси.

402.Плотность газа, состоящего из смеси гелия и аргона при давлении 1,5 атм и температуре 27 °С, равна ρ=2 г/л. Сколько атомов гелия содержится

в1 см3 газовой смеси?

403.Определить среднюю кинетическую энергию <Епост> поступательного движения и среднее значение <Екин> полной кинетической

энергии молекулы водяного пара при температуре Т=600 К. Найти

110