10. Назовите типовые законы регулирования.

В инженерной практике нашли наибольшее применение т. н. типовые алгоритмы (законы регулирования):

1. пропорциональный – П:

r(t)=k_Rε(t).

2. пропорционально - интегральный – ПИ (пропорциональный с воздействием по интегралу (изодромный)):

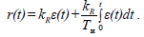
3. пропорциональный с воздействием по интегралу и первой производной – ПИД (пропорционально-интегрально дифференциальный):

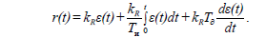
4. интегральный – И:

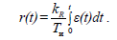
5) пропорциональный с воздействием по первой производной – ПД (пропорционально-дифференциальный):

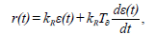
где k_R – коэффициент пропорциональности; T_и – время изодрома (время интегрирования); T_∂ – время предварения.

11. Классификация систем автоматического управления.

Все существующие системы автоматического управления можно классифицировать следующим образом:

1. По принципу управления:

• САУ по возмущению;

• САУ по отклонению;

• комбинированные САУ

2. По алгоритму функционирования:

• системы стабилизации (g(t) = const);

• системы программного управления [g(t)  заданная f(t)];

• следящие системы (g(t)  неизвестная функция).

3. По характеру функционирования:

• обычные;

• адаптивные:

• самонастраивающиеся;

• экстремальные;

• самоорганизующиеся.

4. По виду сигналов:

• непрерывные;

• дискретные:

• цифровые;

• релейные;

• импульсные.

5. По виду математического описания:

• линейные:

• стационарные;

• нестационарные;

• нелинейные:

• стационарные;

• нестационарные.

6. По количеству координат объекта управления:

• одномерные;

• многомерные:

• связанного управления;

• несвязанного управления.

7. По энергии, используемой для перемещения регулирующего органа:

• САУ прямого управления;

• САУ непрямого управления.

12. Что такое динамическое звено.

Динамическим звеном называется часть системы управления, либо вся система, описываемая дифференциальным (или иным) уравнением определенного вида

13. Назовите порядок составления дифференциального уравнения звена.

Порядок составления дифференциального уравнения звена:

1. Определяют входную(-ые) и выходную(-ые) величины (координаты) звена и устанавливают дополнительные факторы, от которых зависит выходная величина.

2. Используя основные законы той отрасли науки и техники, к которой относится исследуемое звено:

• законы Кирхгофа для электрических звеньев;

• законы Ньютона для звеньев механической природы;

• законы сохранения энергии и вещества для гидравлических и пневматических звеньев,

составляют математическое описание звена в форме дифференциального уравнения.

3. Вводят те или иные упрощающие предположения (допущения) с целью упрощения исходного математического описания.

4. При необходимости осуществляют линеаризацию полученного дифференциального уравнения с целью получения линейного дифференциального уравнения звена.