
Лаб_практикум_Вычисл_матем_Кузина-Кошев
.pdf
Задача численного интегрирования состоит в определении значений xi
|
N |
b |
|
и ci таких, чтобы величина DN ( f ) |
ci f (xi ) f (x)dx |
была минималь- |
|
|
i 0 |
a |
|
ной для функции f (x) из заданного класса функций.
При построении квадратурной формулы удобно рассматривать интеграл от a до b как сумму интегралов, заданных на некоторых интервалах
|
b |
i |
[ i, i], то есть |
f (x)dx f x dx. |
|
ai
Каждый интеграл вида f (x)dx сводится к вычислению интеграла
|
|
|
|
|
|
|
|
|
|
|
единичной |
длины |
вида 1 |
|
|
(s)ds |
с помощью следующей замены |
||||
|
f |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
переменной интегрирования: |
|
|
|
|
|
|
|
|||
x ( ) s, |
s [0,1]. |
|
|
|
|
|
|
|
||
При этом получаем: |
|
|
|
|
|
|
|
|
|
|
f (x) f ( ( ) s) |
|
(s); |
d( ( ) s) ( )ds; |
|||||||
f |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
f (x)dx f ( ( ) s)d( ( ) s) ( )1 |
|
(s)ds. |
||||||||
f |
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
Таким образом, достаточно получить формулу для вычисления ин-
теграла 1 f (s)ds , которую затем нетрудно использовать при определении
0
F(a,b) b f (x)dx.
a
Предположим, что на интервале [a, b] задана равномерная сетка, т.е. xi xi 1 h, (h const) , тогда
N xi |
N |
1 |
|
|
N |
1 |
|
|
|
|
||
F(a,b) f (x)dx h f (xi 1 h s)ds h f |
(s)ds I( f ). |
|||||||||||
i 1 x |
i 1 |
0 |
|
|
i 1 |
0 |
|
|
|
|
||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
Будем искать квадратурную формулу в виде |
|
|
|
|
|
|
||||||
1 |
|
|
m |
|
|
|
|
|
|
|||
I f |
|
|
(s)ds Pk |
|
(sk ). |
|
(7.1) |
|||||
f |
f |
|
||||||||||
0k 0
Ввыражении (7.1) 0 s0 s1 ... sm 1. Разбиение интервала [0, 1]
точками sk называется шаблоном квадратурной формулы.
Чтобы построить квадратурную формулу, необходимо определить весовые коэффициенты (веса) Pk и узлы шаблона sk таким образом, чтобы ошибка численного интегрирования была минимальной.
81
Допустим, что задан некоторый шаблон sk . Найдем Pk . Потребуем, чтобы формула интегрирования была точной для любого полинома Pr s
степени r m (где ( m 1) – количество точек шаблона). Для этого необходимо и достаточно, чтобы квадратурная формула была точной для
всех степенных функций s ( m) , так как
P |
(s) a |
0 |
a s a |
|
s2 .... a |
sr . |
|||||||
r |
|
1 |
2 |
|
|
|
|
|
r |
|
|
||
Заметим, что |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
s |
1 |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|||||||
|
I(s ) s ds |
|
|
|
|
|
|
|
. |
||||
|
1 |
|
|
1 |
|||||||||
|
|
|
0 |
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
||||||
Из формулы (7.1) следует, что формула интегрирования будет точной при значениях весов Pk , удовлетворяющих следующей системе уравнений:
P0 P1 Pm 1; |
|
1 |
|
|
|
||||
P0 s0 |
P1s1 Pm sm |
; |
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
2 |
2 |
|
1 |
|
|
||
P0 s0 |
P1s1 |
Pm sm |
|
3 |
; |
|
|||
........................................... |
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
m |
m |
m |
|
|
|
|
||
P0 s0 |
P1s1 |
Pmsm |
|
|
|
. |
|||
m 1 |
|||||||||
|
|
|
|
|
|
|
|||
Эта система является системой линейных алгебраических уравнений с определителем матрицы коэффициентов, называемым определителем Вандермонда.
Как известно, определитель Вандермонда никогда не равен нулю, и полученная система линейных уравнений всегда имеет единственное решение.
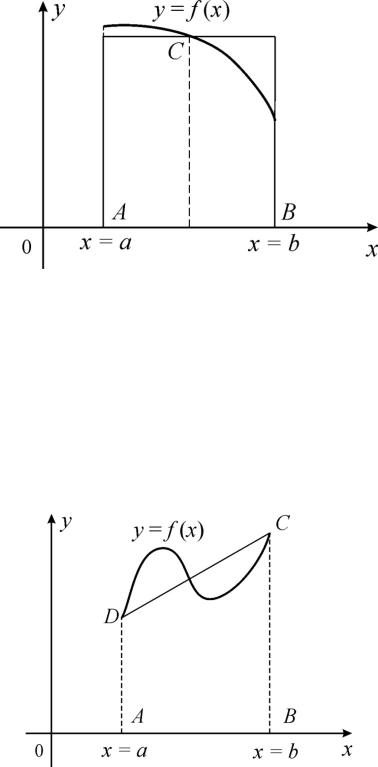
Формула прямоугольников
Если при вычислении интеграла b f (x)dx функцию f (x) заменить на
a
отрезке [a,b] горизонтальной прямой (рис. 14), то получим квадратурную
формулу прямоугольников. Шаблон содержит один узел.
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
m 0, s0 |
|
, P0 1; |
I0 ( f ) f (s)ds P0 f (s0 ) P0 |
|
|
|
||||||||||||||||
2 |
f |
f ; |
||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|||
|
|
N |
1 |
|
|
|
N |
|
|
h |
N |
|
|
|
|
|
|
h |
|
|||
IN f h f (xi 1 hs)ds hf xi 1 |
|
h f xi 1 |
2 |
; |
||||||||||||||||||
|
i 1 |
0 |
|
|
|
i 1 |
|
|
|
2 |
i 1 |
|
|
|
|
|
|
|
|
|||
82
N |
|
|
h |
(7.2) |
|
IN f h f xi 1 |
2 |
. |
|||
i 1 |
|
|
|
|
|
Рис. 14. Иллюстрация метода прямоугольников
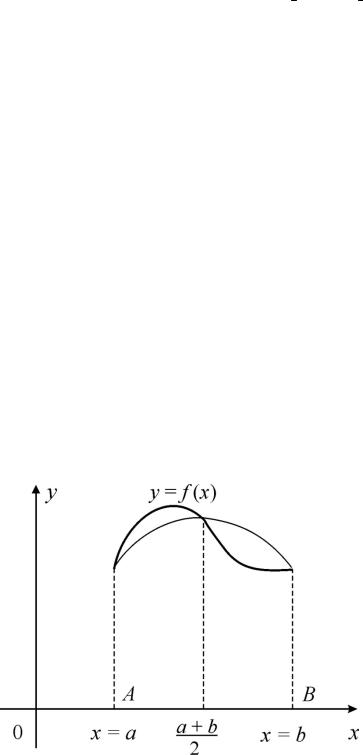
Формула трапеций
Если при вычислении интеграла b |
f (x)dx функцию f (x) заменить |
a |
|
интерполяционным полиномом первой степени (линейная интерполяция), который в узлах x0 a и x1 b принимает соответственно значения f (a)
и f (b) (рис. 15), то получим квадратурную формулу трапеций.
Рис. 15. Иллюстрация метода трапеций
83
Шаблон содержит два узла.
|
|
|
m 1, s |
|
0, s |
1, P |
P 1 ; |
I |
( |
|
) 1 f |
(0) 1 f |
(1); |
||||||||||
|
|
|
0 |
f |
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
0 |
1 |
|
2 |
1 |
2 |
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IN ( f ) 1 h ( f (xi 1 ) f (xi 1 |
h)). |
(7.3) |
||||||||||||||
Таким образом, |
|
|
2 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IN ( f ) h ci f (xi 1 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где c0 cN |
|
1 |
, а все остальные ci 1 |
i 1, , N 1 , то есть |
|||||||||||||||||||
|
|
|
|
2 |
|
|
|
N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
( f ) h |
|
|
|
|
f (x ) f (x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|||
N |
f (x ) 2 |
|
N |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
0 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
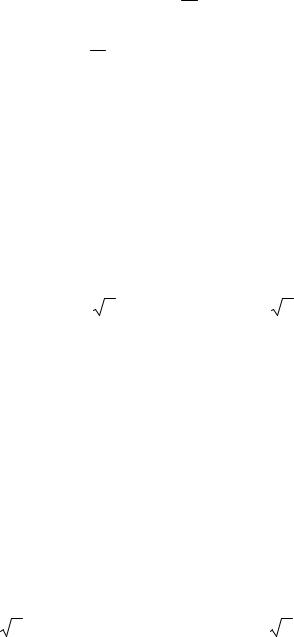
Формула Симпсона (формула парабол) |
||||||||||||||||||
Если при |
вычислении b |
f (x)dx |
функцию |
f (x) |
на [a, b] заменить |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интерполяционным полиномом второй степени, построенным по значе-
ниям функции f (x) в трех узлах x |
|
a , |
x |
|
a b |
, |
x |
|
b , то получим |
0 |
|
2 |
|||||||
|
|
1 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
формулу Симпсона (формулу парабол) (рис. 16).
Рис. 16. Иллюстрация метода парабол
Шаблон содержит три узла.
m 2, s0 0, s1 12 , s2 1.
84
Для определения коэффициентов Pi имеем систему:
|
|
|
|
|
|
|
|
|
|
P |
|
P |
|
1; |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
1 |
1 |
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
P2 |
1 |
; |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
P1 |
2 |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
P |
1 P |
1 1. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
P |
1 , |
|
P |
4 , |
|
P 1 , и, значит, |
|
||||||||||||||||||||||
|
|
0 |
|
|
6 |
|
|
1 |
|
6 |
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
I2 ( f ) |
f |
(0) |
|
|
|
|
f (1). |
|
|||||||||||||||||||||
|
6 |
6 |
f |
2 |
|
6 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда следует квадратурная формула Симпсона: |
|
|||||||||||||||||||||||||||||
IN ( f ) |
1 |
|
|
|
N |
|
|
|
|
|
|
|
4 f |
|
|
|
|
|
|
|
|
1 |
|
|
||||||
6 |
h f (xi 1 ) |
xi 1 |
|
2 |
h f (xi 1 |
|||||||||||||||||||||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(7.4) |
h) . |
|
|
|
Замечание. В формуле Симпсона число узлов обязательно нечетное, т.е. число отрезков четно.
Формулы Ньютона — Котеса
Данный метод основан на замене подынтегральной функции параболой m-го порядка (при m = 1 имеем формулу трапеций, при m = 2 – формулу Симпсона).
Потребуем, чтобы формула интегрирования была точной для полинома Лагранжа Pm (s):
|
m |
|
|
|
Pm (s) lkm (s) f (sk ) , |
|
|
|
k 0 |
|
|
где lkm (s) – интерполяционные коэффициенты Лагранжа. |
|||
Найдем I Pm : |
|
|
|
1 |
1 m |
m |
1 |
I Pm Pm (s)ds lkm (s) f (sk )ds f (sk ) lkm (s)ds. |
|||
0 |
0 k 0 |
k 0 |
0 |
|
1 |
m |
|
Квадратурная формула f s ds |
Pk f sk является точной формулой |
||
|
0 |
k 0 |
|
для интегрирования полинома степени m, если
Pk 1 lkm (s)ds .
0
85
|
|
Формула Котеса для четырехточечного шаблона. Разобьем интервал |
|||||||||||||||||||||||||||||||||||||||||
[0,1] точками |
sk k , |
k 0,1, 2, 3 |
(число интервалов кратно трем), то есть |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
s |
0 |
0, s 1, s |
2 |
2 , s 1; |
m 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
3 |
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
s |
3 |
s |
3 |
s |
|
|
|
|
|
1; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
8 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
3 |
0 |
3 |
0 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 s 0 s |
|
3 |
s 1 |
|
|
|
|
|
|
3; |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
8 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
0 |
3 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Аналогично |
P |
3; |
|
P 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
8 |
|
3 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
I3 ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (1) |
|
||||||||||||||||||||
|
|
|
|
f (0) 3 f |
|
3 |
|
|
3 f |
3 |
|
; |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.5) |
||
|
|
IN f |
N 1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
8 |
h f xi |
3 f xi |
3 |
h 3 f xi |
3 |
h |
f xi 1 h . |
|
||||||||||||||||||||||||||||||||
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Метод Ньютона – Котеса является обобщением рассмотренных нами методов численного интегрирования. Весовые коэффициенты не зависят от функции, зависят от количества точек шаблона. Выпишем их значения:
m 1, |
P |
P 1 – метод трапеций; |
|
|
|
|
|
|
|
||||||||||
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
P 1 , |
|
4 , |
P 1 |
|
|
|
|
|
|
|
|
|
||||||
m 2, |
P |
– метод Симпсона. |
|||||||||||||||||
|
0 |
6 |
1 |
|
6 |
|
2 |
6 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Метод Ньютона – Котеса соответственно для четырех-, пяти- и |
|||||||||||||||||||
шеститочечного шаблона: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
m 3, P P 1, |
P P 3 |
; |
|
|
|
|
|
|
|
|
|||||||||
|
0 |
3 |
8 |
|
1 |
|
2 |
8 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m 4, P P |
7 |
, |
P P 32, |
P |
2 |
|
; |
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||||
|
0 |
4 |
90 |
|
1 |
|
|
3 |
90 |
2 |
15 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
m 5, P P |
|
19 |
, P P 25, |
P P |
|
25 |
. |
||||||||||||
288 |
|
||||||||||||||||||
|
0 |
5 |
|
1 |
|
4 |
96 |
|
2 |
|
3 |
144 |
|||||||
86
Наиболее употребляемой среди квадратурных формул Ньютона – Котеса является формула Симпсона, поскольку она точна для полиномов не только второй, но и третьей степени.
Квадратурная формула Чебышева
Во всех предыдущих методах интервал интегрирования делился на равные участки, а весовые коэффициенты (в общем случае) были различны. Для некоторых задач хорошей точности метода численного интегрирования можно добиться исходя из оптимального выбора узлов интегрирования. Предположим, что все коэффициенты Pi квадратурной
формулы равны одной и той же константе Pi m1 , то есть
I f 1 m f (si ) . m i 1
Как и при построении предыдущих квадратурных формул, потребуем точности формулы интегрирования для одночленов 1, s, s2 , s3 , ..., sN .
Получим систему уравнений для определения si:
sk sk ... sk |
|
m |
|
|
, k 1, 2, ..., m. |
||
k |
1 |
||||||
1 2 |
m |
|
|
||||
Решая эту систему нелинейных алгебраических уравнений, можно получить значения неизвестных si узлов разбиения интервала интегрирования.
Например, при m = 3 формула Чебышева имеет вид:
1 |
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
||||
f (x)dx J3[ f ] |
|
|
2 |
|
|
|
|
|
2 |
(7.6) |
|||||||||||||||||||
3 |
f |
2 |
4 |
|
f |
2 |
|
f |
2 |
4 |
. |
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Запишем формулу для всего интервала интегрирования [a, b].
Пусть {xi} – разбиение интервала [a, b], x a (b a)s, xi xi 1 h . Тогда
b |
N xi |
N |
1 |
|
|
N |
m |
||
F(a,b) f (x)dx f (x)dx h |
|
|
|
|
|
||||
f |
(s)ds h Pk f (sk ) |
||||||||
a |
i 1 x |
i 1 |
0 |
|
|
i 1 |
k 0 |
||
|
i 1 |
|
|
|
|
|
|
|
|
N |
m |
N |
m |
|
|
|
|
||
h Pk f (xi 1 hsk ) h Pk f (xi 1 hsk ). |
|||||||||
i 1 |
k 0 |
i 1 k 0 |
|
|
|
|
|||
Для трехточечного шаблона формула Чебышева имеет вид:
|
h |
N |
|
|
|
1 |
|
1 |
|
f xi h |
2 |
4 |
|||||
|
3 i 1 |
|
|
|
|
|||
IN f b |
f (x)dx |
|
|
|
|
|
|
|
||||
|
|
a |
|
|
|
|
|
|
|
|
|
(7.7) |
|
|
|
|
h |
|
1 |
|
1 |
|
|
||
2 |
|
|
2 |
|
||||||||
|
f xi |
|
f xi h |
2 |
4 |
. |
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
||
87
Квадратурная формула Гаусса
Для получения квадратурной формулы отыскиваются оптимальные значения узлов интегрирования si и коэффициентов ci квадратурной
m
формулы I f ci f (si ) одновременно.
i 0
Потребуем точности формулы для полиномов степени, меньшей либо равной ( 2m 1).
Учитывая, что |
|
|
I(sm ) 1 smdx |
sm 1 |
|
|
1 |
|
|
1 |
|
|
, получим систему |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
m 1 |
|
|
m 1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
||||||||||
( 2m 2) алгебраических уравнений с ( 2m 2) неизвестными: |
|||||||||||||||||||||||||||||
c |
0 |
c ..... c |
m |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
c |
|
s |
|
c s |
..... c |
m |
s |
m |
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
0 |
|
|
1 1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||
c0 s0 |
|
c1s1 |
..... cm sm |
|
3 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
............................................ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2m 1 |
|
|
|
2m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
2m 1 |
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
c |
0 |
s |
0 |
|
|
c s |
|
|
..... c |
m |
s |
m |
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(m 1) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Например, при m = 2 получим следующую формулу:
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
8 |
|
|
(s1 ) |
5 |
|
|
|
(s2 ) , |
|
||||||||||||
|
|
|
|
|
|
|
f |
(s)ds J3 |
[ f ] |
|
|
f |
(s0 ) |
|
|
f |
f |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
18 |
|
18 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
||||||||
где s |
0 |
1 |
|
0,6 , |
|
|
s |
|
1 , |
s |
2 |
1 |
|
0,6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Аналогично формуле Чебышева можно записать: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
IN f b |
f (x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
N |
|
|
|
|
|
|
1 |
0,6 |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
1 |
0,6 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
f |
x |
|
|
|
|
|
|
|
|
|
f |
x |
|
|
|
|
|
f |
x |
|
|
|
|
|
. |
|||||||||||||||
18 |
|
h |
|
2 |
|
|
|
|
|
|
2 |
|
h |
|
|
2 |
|
|||||||||||||||||||||||||||
|
i 1 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(7.8)
(7.9)
Оценки погрешности квадратурных формул
Существуют следующие оценки погрешности квадратурных формул
|
N |
b |
|
DN ( f ) |
ci f (xi ) f (x)dx |
, полученные на основе разложения интегри- |
|
|
i 0 |
a |
|
руемой функции в ряд Тейлора, и оценки остаточного члена разложения.
88
Для формулы прямоугольника
DN f |
h2 |
|
DN f |
|
h2 |
(b a)max f |
|
|||||||
24 |
f ( )(b a) ; |
24 |
( ) ; (7.10) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
здесь и далее – некоторая точка [a,b]; |
|
h – шаг интегрирования. |
||||||||||||
Для формулы трапеций |
h2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
DN f |
f |
|
|
|
|
|
|
|
(7.11) |
|||
|
|
12 |
|
( )(b a) . |
|
|||||||||
Для формулы Симпсона |
|
|
|
|
|
|
|
|
|
|
||||
|
b a |
|
|
|
|
|
|
|
||||||
|
|
DN f |
h |
4 |
f |
|
|
|
(7.12) |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
180 |
|
|
( ) . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, что точное значение интеграла в методе прямоугольников можно получить только при f (x) – кусочно-постоянной, а в методе
трапеций – при f (x) линейной или кусочно-линейной функции.
Пример 2 7 .
|
|
1 |
dx |
|
|
Вычислить I 0 |
по формулам Ньютона – Лейбница, трапеций и |
||
|
1 x2 |
|||
Симпсона. |
|
|
||
|
Решение. |
|
|
|
1 |
По |
формуле |
Ньютона – Лейбница получим точное значение |
|
dx |
0,785398 . |
|
|
|
2 |
|
|
||
0 |
1 x |
|
|
|
Разобьем интервал интегрирования на 10 равных частей ( k 10). Для вычисления интеграла по формулам трапеций и Симпсона составляем табл. 23 значений подынтегральной функции f (x) в точках разбиения
интервала интегрирования [0, 1]:
Таблица 2 3
x |
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
|
0,7 |
0,8 |
0,9 |
f(x) |
1 |
0,9901 |
0,9615 |
0,9174 |
0,8621 |
0,8 |
0,7353 |
0,6711 |
0,6098 |
0,5525 |
||
|
Подставляя найденные значения в формулы (7.3) и (7.4), получим |
|||||||||||
соответственно I 0,78498 (по формуле трапеций) и I |
0,78539 (по фор- |
|||||||||||
муле Симпсона).
Отметим, что результат, полученный по формуле Симпсона, существенно точнее.
Пример 2 8 .
Вычислить методом Симпсона 2 x2dx , разбив [1, 2] на 4 части.
1
89
Решение.
Определим шаг: h 2 1 0,25. 4
Вычислим интеграл по формуле (7.4):
|
|
|
|
|
|
|
|
2 |
x2 dx |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0,25 |
12 |
4 |
(1 0,125)2 |
1,252 1,252 |
4 (1,25 0,125)2 1,52 |
|
|
|
||||
6 |
|
|
1,52 |
4 (1,5 0,125)2 |
1,752 1,752 4 (1,75 0,125)2 |
22 |
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,333.
Значение совпадает со значением, полученным в системе MathCAD.
Пример 2 9 .
Вычислить определённый интеграл
I 1 sin(0,5x 1)2 dx
0
всеми рассмотренными способами.
Решение.
Разобьем интервал интегрирования на 10 равных частей ( k 10):
|
|
|
|
|
|
|
|
|
|
|
|
h b a |
1 0 |
0,1. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вычисления интеграла составим табл. 24 значений подынтег- |
|||||||||||||||||||||||||||||
ральной функции в точках разбиения интервала интегрирования. |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 4 |
|||
xi |
|
0 |
|
0,1 |
|
0,2 |
|
0,3 |
|
0,4 |
0,5 |
|
|
|
0,6 |
|
|
0,7 |
|
0,8 |
0,9 |
|
1 |
||||||
f(xi) |
0,708 |
0,752 |
0,794 |
0,833 |
0,869 |
0,9 |
0,928 |
0,952 |
0,971 |
0,985 |
0,995 |
||||||||||||||||||
Используя простейшие квадратурные формулы численного интегриро- |
|||||||||||||||||||||||||||||
вания, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1) по формуле прямоугольников (7.2): |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
I 0,1 sin 0,5 xi 1 |
|
|
|
|
|
1 |
|
0,884249; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) по формуле трапеций (7.3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
I 0,1 sin 0,5xi 1 1 2 sin 0,5 xi 1 0,1 1 2 0,883769; |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3) |
|
по формуле Симпсона (7.4): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
0,1 |
10 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
0,1 |
|
2 |
|
|
2 |
|
||||||
I |
|
|
|
sin 0,5xi 1 |
1 |
4sin 0,5 xi 1 |
|
|
|
|
1 |
sin 0,5xi 1 |
|
||||||||||||||||
6 |
2 |
|
|||||||||||||||||||||||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,884089; |
|
|
|
|
|
|
|
|
|
|
|||||
90
