Лаб_практикум_Вычисл_матем_Кузина-Кошев

Добавил:

sergeis2077 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

Вычислительная математика

Файл:

f (x) ex x 2

f (a) 0.058038

f (b) 0.044074

f (z) 7.292781 10

.pdf

Скачиваний:

Добавлен:

03.02.2018

Размер:

1.53 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 134 5 6 7 8 9 10 11 12 13 > Следующая >>>

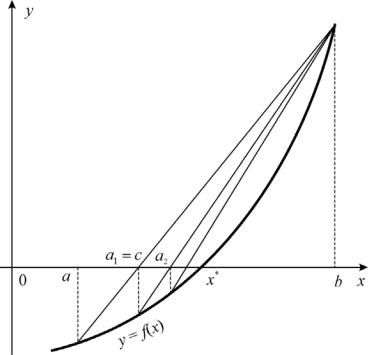
Рис. 3. Иллюстрация метода хорд

Если про вторую производную функции f (x) ничего не известно, то

метод хорд позволяет построить аналогичную итерационную схему, но после определения точки с интервал, на котором происходит дальнейшее определение корня, выбирается из условия противоположности знаков функции f (x) на его концах.

Метод Ньютона (метод касательных)

Метод Ньютона (метод касательных) аналогичен методу хорд, но в качестве прямой берется касательная к кривой в точке начального приближения (рис. 4).

Метод касательных применим только в случае, если функция f (x) не

имеет на интервале [a, b]

точек перегиба,

то есть

f (x) сохраняет знак.

Точку

или b),

из которой

начинается

схема

метода касательных,

выбираем из условия

0 .

f ( ) f ( )

Запишем

уравнение

касательной, выходящей

из точки (b,

f(b)):

y f (b)

k f (b) ,

где k – тангенс угла наклона касательной к оси Ox.

x b

Пусть (0, d) – точка пересечения касательной и оси Ox, тогда d b

f (b)

и итерационная схема метода касательных записывается в виде:

f (b)

b b,

f (bn 1 )

b .

(3.3)

f (bn 1 )

n 1

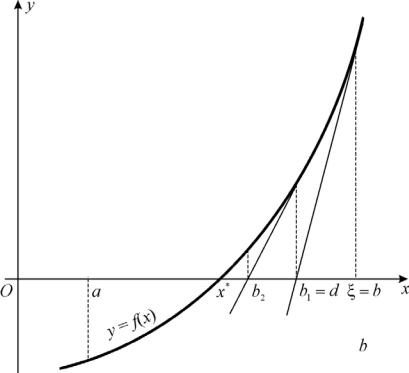
Рис. 4. Иллюстрация метода касательных

Комбинированный метод хорд и касательных

Комбинированный метод хорд и касательных (рис. 5) является одним из наиболее используемых методов поиска корней алгебраических уравнений. Идея метода состоит в одновременном применении метода хорд и метода касательных, которые дают приближение положительного корня с разных сторон. Комбинированный метод удобно использовать, если на отрезке [a, b], содержащем только один корень, вторая производная f x

сохраняет знак. Постоянство знака f x означает, что кривая либо выпуклая ( f x 0), либо вогнутая ( f x 0 ).

Рассмотрим 4 различных случая поведения функции на отрезке [a, b], в

зависимости от знака производных.
В 1-м	случае (рис.	5, а),	когда на отрезке [a, b] функция f (x)
монотонно	возрастает, f		0 , а кривая y f (x) вогнута,		,
		x		f x 0

имеем: касательная пересекает ось Ox со стороны выпуклости (справа), а хорда – со стороны вогнутости графика функции y f (x) , слева.

Абсциссы точек пересечения вычисляются по формулам:

ak 1 ak ak ;

bk 1 bk bk

k 0,1, 2, ,

(3.4)

где a

bk ak f ak

f bk

f bk f ak

f bk

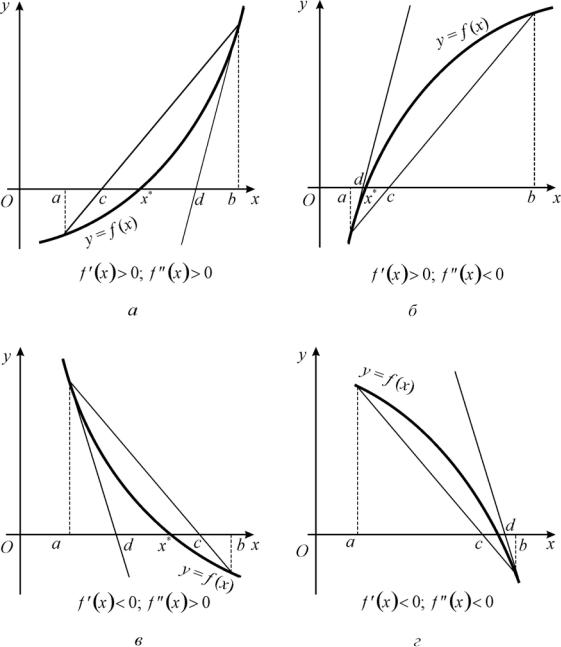
Рис. 5. Иллюстрация комбинированного метода хорд и касательных

Процесс вычисления заканчивается на m-м приближении, когда вы-

полняется неравенство	am bm	,	где – точность вычислений, в

качестве корня определяется величина			x* am bm .
			2

Аналогично использование формул для случая 4 (рис. 5, г), когда
функция f (x) монотонно убывает: f	x 0 , а кривая	y f (x) вогнута:

f x 0 .

Во 2-м случае (рис. 5, б), когда на отрезке [a, b] функция f (x)

монотонно возрастает:		, а кривая	y f (x) выпукла:	f		,
	f x 0				x 0

касательная пересекает ось Ox слева, а хорда – справа. 33

Абсциссы точек пересечения вычисляются по формулам:

ak 1

ak ak ;

bk 1 bk bk

k 0,1, 2, ,

(3.5)

где a

f ak

ak f bk

f bk f ak

f ak

Аналогично использование формул для случая 3 (рис. 5, в), когда

функция f (x) монотонно убывает: f x 0 ,

а кривая y f (x)

вогнута:

f x 0 .

Пример 5 .

1.Выделить отрезок, в котором лежит корень уравнения lg x x2 0 .

2.Определить корень на выделенном отрезке методами простой итерации, половинного деления, комбинированным методом хорд и касательных.

Решение.

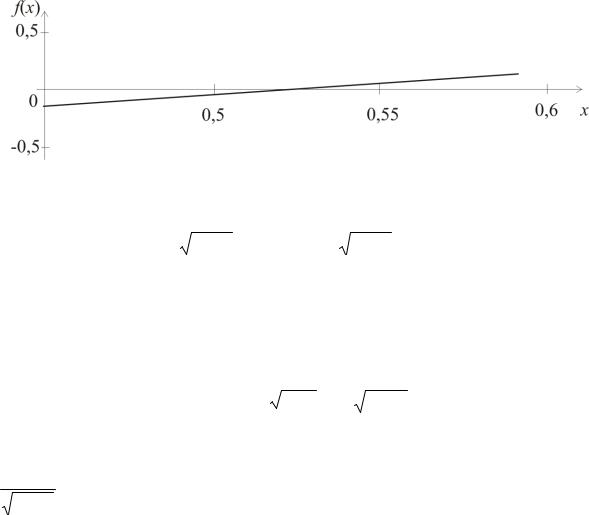
Построив график функции f (x) lg x x2 (рис. 6), определим интервал, в котором находится корень заданного уравнения: 0,5; 0,55 .

	Рис. 6. Отделение корня уравнения
Для решения	методом		простой итерации		уравнение lg x x2	0
приведем к виду	x	lg x ,	т.е. (x)	lg x .	Заметим, что в правой

части формулы x 1, следовательно, lg x 0.

Проверим сходимость итерационного процесса, для чего определим

max

(x)

x 0.5, 0.55

Из формулы

(x)

ln10

lg x

видно,

что

возрастает на

интервале

0,5; 0,55 , т.к. функции

(x)

1убывают с возрастанием x.

lg x

А поскольку

убывает

на

этом

интервале и,

(x) 0 , то

(x)

соответственно,

max

0,7916

что

обеспечивает

(x)

(0,5)

x 0.5, 0.55

сходимость метода, причем немонотонную.

0,5 0,55 0,525 ,

В качестве начального приближения выберем

x(0)

зададим точность решения =0,001. Тогда

x x

(1)

(2)

log(x(0) ) log(0,525) 0,529;

log(x(1) ) log(0,529) 0,5259;

x(3)	log(x(2) )			log(0,5259) 0,526				и т.д.
Все вычисления сведены в табл. 2.										Таблица 2
										Таблица 2
i		0		1	2	3	4	5	6		7	8
x(i)		0,525	0,529		0,5259	0,526	0,5282	0,5265	0,5278		0,5268	0,5276
(x(i) )		0,529	0,5259		0,526	0,5282	0,5265	0,5278	0,5268		0,5276	0,527
x(i 1)		0,529	0,5259		0,526	0,5282	0,5265	0,5278	0,5268		0,5276	0,527
x(i 1)

Решение x 0,527 получаем на 8-й итерации.

Методом половинного деления найдем корень на выделенном отрезке,

для чего вычислим zk ak 1 bk 1 .
		2	P	f (ak 1 ) f (zk ) :
Рассматриваем		произведение	P	f (ak 1 ) f (zk ) :				если	P 0 , то
принимаем ak zk , bk bk 1 , иначе ak ak 1					и bk zk .
Процесс заканчивается при таком m , когда						am bm	2 .
Процесс заканчивается при таком m , когда						am bm	2 .
Все вычисления сведены в табл. 3.								Таблица 3
								Таблица 3
a, b	x	f(x)	zk		f(zk)			P	am bm
a	0,5	–0,05103	0,525		–0,004216			+	0,05
b	0,55	–0,05103	0,525		–0,004216			+	0,05
b	0,55
a1	0,525	–0,004216	0,5375		0,019284			–	0,025
b1	0,55	–0,004216	0,5375		0,019284			–	0,025
b1	0,55
a2	0,525	–0,004216	0,5313		0,007525			–	0,00625
b2	0,5375	–0,004216	0,5313		0,007525			–	0,00625
b2	0,5375
a3	0,525	–0,004216	0,5281		0,001627			–	0,003125
b3	0,5313	–0,004216	0,5281		0,001627			–	0,003125
b3	0,5313
a4	0,525	–0,004216	0,5265		–0,00128			+	0,00156
b4	0,5281	–0,004216	0,5265		–0,00128			+	0,00156
b4	0,5281
a5	0,5266								0,00078
b5	0,52812								0,00078
b5	0,52812

Корень заданного уравнения x 0,527.

Решим задачу комбинированным методом хорд и касательных. Абсциссы точек пересечения вычислим по формулам (29). Процесс вычисления заканчивается на m -м приближении, когда выполняется соотно-

шение		am bm	.
шение		am bm	.
Все вычисления сведены в табл. 4.								Таблица 4
								Таблица 4
a, b		x		lg x	x2	lg x x2	Поправки		am bm
a	0,50			–0,3010	0,25	–0,05103	–0,02717		0,05
b	0,55			–0,2596	0,3025	0,04286	0,022682		0,05
b	0,55			–0,2596	0,3025	0,04286	0,022682
a1	0,52717			–0,2780	0,2779	–0,00014	–0,0000723		0,00014
b1	0,52731			–0,2779	0,2781	0,000122	0,00004815		0,00014
b1	0,52731			–0,2779	0,2781	0,000122	0,00004815
a2	0,52724								0,000019
b2	0,52726								0,000019
b2	0,52726

Корень заданного уравнения x 0,527.

Пример 6 .

1. Графическим способом определить отрезок [a, b], в котором нахо-

дится действительный корень уравнения ex x 2 0 и приближенное значение корня.

2.Вычислить корень уравнения с точностью 1 10 4 методом половинного деления, комбинированным методом и с использованием системы

MathCAD.

3.Оценить скорость сходимости метода Ньютона.

Решение.

1) Построив график функции f x ex x 2 в системе MathCAD (рис. 6),

определим интервал, в котором находится корень заданного уравнения.

f(x) ex x 2

0.4

0.2

f(x) 0

0.2

0.4

0.42

0.43

0.44

0.45

0.46

Рис. 6. Графический способxопределения интервала нахождения корня уравнения

[a, b] [0.42; 0.46]. Приближенное значение корня x 0,44.

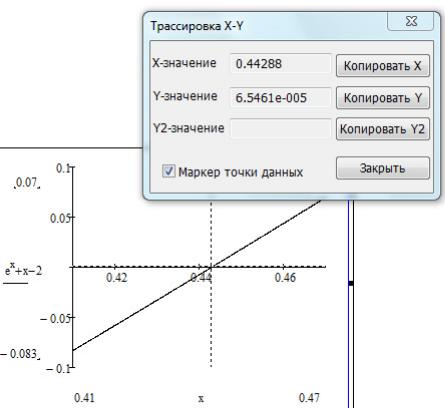
Графическое решение уравнения: Format Graph Trace (рис. 7). Чтобы найти корень уравнения графически, необходимо включить трассировку в меню «Формат» и установить маркер в точке пересечения графика с осью абсцисс. В окне диалога отобразятся координаты маркера.

		Рис. 7. Графический способ определения корня уравнения
	2) Решим уравнение методом половинного деления.
	Найденный		отрезок делим		пополам	точкой	zk ak 1 bk 1	ak 1	и
вычисляем f zk . Если				P f ak 1 f zk 0 , то принимаем				2
вычисляем f zk . Если				P f ak 1 f zk 0 , то принимаем				ak zk ,
bk bk 1,		иначе	ak ak 1	и	bk zk .	Процесс	заканчивается, когда
	am bm	.
	am bm	.

Фрагмент вычислений в среде MathCAD:

a z

		z a		b a			z 0.45	f (z) 0.018312
	b z			2
	b z			b a
				b a						3
		z a		2			z 0.445	f (z) 5.490196 10
	b z и т.д.					0.0001 0.4428 – корень уравнения.
	На 9-й итерации				a b
	На 9-й итерации				a b
	Все вычисления сводим в табл. 5.									Таблица 5
										Таблица 5
a,b		x			f x		zk	f zk	P	am bm
a		0,42		–0,058			0,44	–0,0072	+	0,04
		0,42
b		0,46
b		0,46
a1		0,44		–0,0072			0,45	0,018	–	0,02
b1		0,46		–0,0072			0,45	0,018	–	0,02
b1		0,46
a2		0,44		–0,0072			0,445	0,054	–	0,01
b2		0,45		–0,0072			0,445	0,054	–	0,01
b2		0,45
a3		0,44		–0,0072			0,4425	–0,0009	+	0,005
b3		0,445		–0,0072			0,4425	–0,0009	+	0,005
b3		0,445
a4		0,4425		–0,0009			0,44375	0,0022	–	0,025
b4		0,4425		–0,0009			0,44375	0,0022	–	0,025
b4		0,4425
a5		0,4425		–0,0009			0,443125	0,000692	–	0,00125
b5		0,44375		–0,0009			0,443125	0,000692	–	0,00125
b5		0,44375
a6		0,4425		–0,0009			0,4428125	–0,000107	+	0,00625
b6		0,443125		–0,0009			0,4428125	–0,000107	+	0,00625
b6		0,443125
a7		0,4428125	–0,000107				0,44296875	0,000292	–	0,0003125
b7		0,443125	–0,000107				0,44296875	0,000292	–	0,0003125
b7		0,443125
a8		0,4428125	–0,000107				0,442890625	–0,000093	-	0,00015625
b8		0,44296875	–0,000107				0,442890625	–0,000093	-	0,00015625
b8		0,44296875
a9		0,4428125								0,000078125
b9		0,442890625								0,000078125
b9		0,442890625

3) Решим уравнение ex x 2 0 комбинированным методом хорд и

касательных в среде MathCAD. f (x) ex x 2

a 0.42 b 0.46

f (a) 0.058038

f (b) 0.044074

Определим аналитически первую производную функции и найдем ее

значения на концах интервала.

x 2

f (a)

2.521962

f (b )

2.584074

метод

слева –

метод

f b f

справа применяем

касательных,

хорд:

(b a)f (a)

a1 a

f (b) f (a)

a1 0.442735

b1 b

f (b)

b1 0.442944

a a1

b b1

a2 a

(b a)f (a)

a2 0.442854

f (b) f (a)

b2 b

f (b)

b2 0.442854

f (b)

b2 a2

0.442854

0 1 10 4

0.442854 –

корень

урав-

нения.

4) Оценим скорость сходимости метода Ньютона.

Известно,

что

итерационный процесс

x(n)

x(n 1)

сходится

при

n , если max

(x)

x a,b

f (x)

Итерационная

схема

метода

Ньютона

(x) x

т.е.

f (x)

(x)

. После подстановки в последнюю формулу функции

f x ex

f (x)

x 2 , а также ее первой и второй производных, получим:

(ex x 2) ex

(x)

ex 1 2

(0,46) 0,027

На

концах

интервала (0,42) 0,035 ,

max

1, что говорит о хорошей сходимости метода Ньютона.

x 0,42, 0,46

Пример 7 .	56 x графическим способом определить
1. Для функции f (x) (28 x)3

отрезок [a, b], в котором находится действительный корень уравнения

f(x) 0 и приближенное значение корня.

2.Вычислить корень уравнения с точностью 1 10 3 с использованием системы MathCAD методами простой итерации, половинного деления и комбинированным.

3.Оценить скорость сходимости метода Ньютона.

Решение.
1)	Графический метод отделения корней (рис. 8).
				2
	0.06	0.04	0.02	0	0.02	0.04	0.06
				2
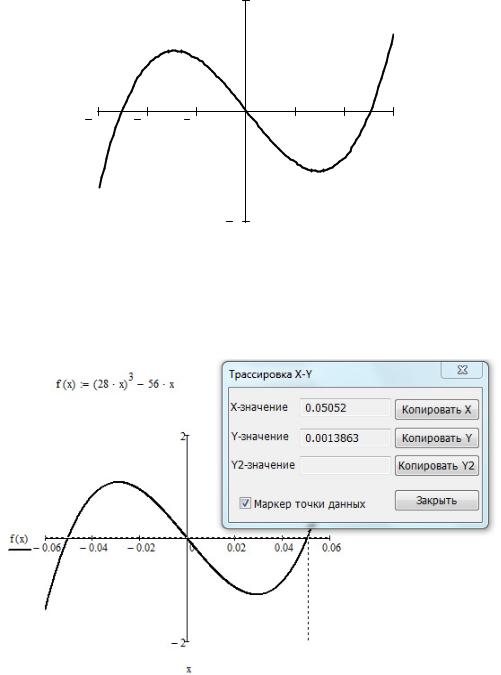
	Рис. 8. Графический способ отделения корней уравнения

Как видно из графика, уравнение имеет 3 корня: 1-й корень в интер-

вале [– 0,06; – 0,04], 2-й – в [– 0,01; 0,01], 3-й – в [0,04; 0,06]. Уточним ко-

рень, находящийся внутри 3-го интервала различными методами. На рис. 9 представлено графическое решение уравнения: Format Graph Trace.

Рис. 9. Графический способ определения корня уравнения

<<< < Предыдущая 1 2 34 / 134 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете Вычислительная математика

#
03.02.20187.71 Кб11Итерация.xlsx
#
03.02.20181.24 Mб5КП.docx
#
03.02.20181.12 Mб7КП.pdf
#
03.02.201833.55 Кб10Кп.xlsx
#
03.02.20187.08 Кб12Крамер.xlsx
#
03.02.20181.53 Mб29Лаб_практикум_Вычисл_матем_Кузина-Кошев.pdf
#
03.02.20187.03 Кб8Обратка.xlsx
#
03.02.20184.18 Mб43УП_Вычисл_матем_Кузина-Кошев.pdf