
Лаб_практикум_Вычисл_матем_Кузина-Кошев
.pdf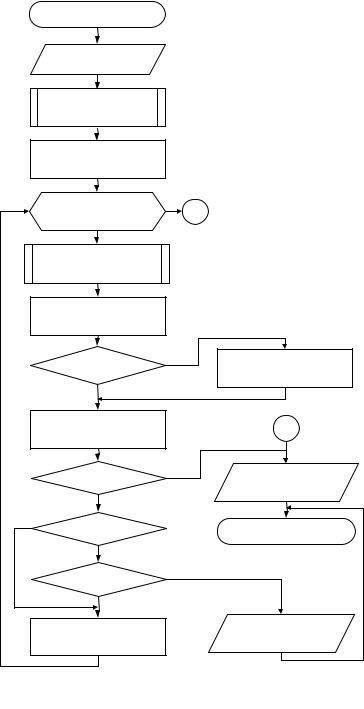
Продолжение прил. 1 Метода Гаусса или метод последовательного исключения неизвестных относится к прямым методам решения СЛАУ и основан на приведении матрицы коэффициентов A(i,j) к треугольному виду – прямой ход;
обратный ход – последовательное нахождение неизвестных (рис. 1-П). Входные данные: N – число уравнений; A(i,j) – массив коэффициентов
системы; B(i) – массив свободных членов.
Выходные данные: X(i) – массив неизвестных – решения СЛАУ.
Блок-схема алгоритма метода Зейделя
Рис. 2-П. Блок-схема алгоритма метода Зейделя |
111 |

Продолжение прил. 1 Метод Зейделя относится к итерационным методам решения СЛАУ
(рис. 2-П).
Входные данные:
n – число уравнений, число неизвестных;
aij – матрица коэффициентов системы; bi – столбец свободных членов; e – погрешность.
Выходные данные:
xi –решение; k – число итераций.
Блок-схемы алгоритмов итерационных методов решения нелинейных уравнений
Блок схема алгоритма метода отделения корня
Входные данные (рис. 3-П): XN – начальное значение координаты, от которого производится поиск; DX – шаг изменения.
Выходные данные: LG и PG – левая и правая границы интервала.
|
|
|
Начало |
|
|
|
|
|
|
XN, DX |
|
|
|
|
|
|
|
|
|
|
|
|
Y1=f (XN) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y2=f (XN+DX) |
|
|
|
|
|
|
|
|
|
|
|
Нет |
|
Y1*Y2<0 |
Да |
|||
|
|
|
|
|
||
|
|
|
|
|
|
LG=XN |
Y1=Y2 |
|
|
|
|
|
|
|
|
|
|
|
|
PG=XN+DX |
XN=XN+DX Конец
Рис. 3-П. Блок-схема алгоритма метода отделения корня
112

Продолжение прил. 1
Блок схема алгоритма метода простых итераций
Входные данные (рис. 4-П): a и b левый и правый концы интервала; e – погрешность.
Выходные данные: x – решение.
Начало |
|
Ввод x, e |
|
y = F(x) |
|
tmpX = x |
|
x = y |
|
|x-tmpX| ≤ e |
Нет |
|
|
Да |
|
Корень x ± e |
|
Конец |
|
Рис. 4-П. Блок-схема алгоритма метода простых итераций
113

Продолжение прил. 1
Блок схема метода половинного деления
Входные данные (рис. 5-П): a и b левый и правый концы интервала; e – погрешность.
Выходные данные: x – решение.
Начало |
a, b, e |
Нет |
f (a)·f(b) < 0 |
Да |
x = (a + b) / 2 |
|
|
|
Да |
|
|
|
|
|||
x – точное |
|
|
|
|
||||||
решение |
|
f (x) = 0 |
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
Да |
|
|
|
|
|||
|
|
|
|
b - a ≤ e |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Нет |
Да |
|
|||
|
|
|
|
|
|
|||||
Корень x ± e |
|
f (a)·f(x) < 0 |
|
|
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
Нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Конец |
|
|
|
|
|
|
|
|
||
|
a = x |
|
b = x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5-П. Блок-схема алгоритма метода половинного деления
114

|
Продолжение прил. |
1 |
Блок схема алгоритма метода хорд |
|
|
Входные данные (рис. 6-П): xa и xb – левый и правый концы интервала; |
||
e – погрешность. |
|
|
Выходные данные: xn – решение. |
|
|
|
Начало |
|
|
xa, xb, e |
|
Нет |
Да |
|
|
f (b)·f "(b) > 0 |
|
V = xa, x=xb, |
V = xb, x=xa, |
|
FV=f(xa) |
FV=f(xb) |
|
Нет |
Да |
|
|
V = xb |
|
xn = a + |
xn = x - |
|
+ (FV(x-xa))/(FV-f(x)) |
- (f(x)(xb-x))/(FV-f(x)) |
|
Нет |
|xn - x| ≤ e |
|
|
|
|
|
Да |
|
x = xn |
Корень xn |
|
|
Конец |
|
Рис. 6-П. Блок-схема алгоритма метода хорд |
|
|
115

Продолжение прил. 1
Блок схема метода Ньютона (касательных)
Входные данные (рис. 7-П): x0 – точка начального приближения; e – погрешность.
Выходные данные: x – решение.
Рис. 7-П. Блок-схема алгоритма метода Ньютона (касательных)
Блок-схемы алгоритма метода Ньютона для решения СНУ
На рис. 7-П, иллюстрирующем алгоритм итерационного метода Ньютона для решения СНУ, используются следующие обозначения:
fi – заданные функции fi x1, x1, , xn ;
fij – частные производные fi x1, x1, , xn  x j ;
x j ;
x – поправка для приближения корня, вычисляется из матричного уравнения f (k 1) x(k) f (k 1) .
Входные данные: n – число уравнений; M – число итераций; xi – вектор начальных приближений; e – погрешность.
Выходные параметры: xi – вектор решений, k – число итераций.
П р и м е ч а н и е .
Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы. Практически метод Ньютона применяется для уточнения решения полученного каким-либо другим методом.
116

Продолжение прил. 1
Рис. 7-П. Блок-схема алгоритма метода Ньютона
117

Продолжение прил. 1
Блок-схема алгоритма интерполирования функций методом Лагранжа
На рис. 8-П приведен алгоритм интерполирования функции методом Лагранжа.
Входные данные: массивы X и Y, общее число пар n.
Выходные данные: L(X) – массив значений полинома Лагранжа в узлах интерполирования.
Начало |
|
X |
n |
|
L = 0 |
|
|
|
I=0, N |
|
|
|
|
I = 0,N |
X(I),Y(I) |
|
L1= C(I) |
|
|
|
I=0, N |
|
|
|
|
J= 0, N |
S(I)=1 |
да |
нет |
|
||
|
|
I=J |
L1 = L*(X-X(J))
J=0, N
L=L+L1
да нет
I=J
L(X) = L1
S(I) = S(I) (X(I)-X(J))
|
|
|
Конец |
|
C(I) = Y(I) / S(I) |
||
|
|
|
|
|
|
|
|
Рис. 8-П. Блок-схема алгоритма метода Лагранжа
118

Продолжение прил. 1
Блок-схемы алгоритмов численного интегрирования Блок схема алгоритма метода прямоугольников
b
На рис. 9-П приведен алгоритм расчета интеграла S f (x)dx
a
методом прямоугольников.
Входные данные: a и b минимальное и максимальное значения интервала интегрирования, n – количество разбиений.
Выходные данные: S – решение.
Начало
a, b, n
h = (b - a) / n
S = S+f (a + (i-1)h)h i = 1, n
S
Конец
Рис. 9-П. Блок-схема алгоритма метода прямоугольников
Блок схема алгоритма метода трапеций
На рис. 10-П приведен алгоритм расчета определенного интеграла методом трапеций.
Входные данные: a и b минимальное и максимальное значения интервала интегрирования, n – количество разбиений.
Выходные данные: I – решение.
119

Продолжение прил. 1
Начало
a, b, n
h = (b - a) / n
S = S+f (a+(i-1)·h)+ + f (a+ i·h); i = 1, n
I = S ·h / 2
I
Конец
Рис. 10-П. Блок-схема алгоритма метода трапеций
Блок схема алгоритма метода Симпсона
На рис. 11-П приведен алгоритм расчета определенного интеграла
b
S f (x)dx методом Симпсона.
a
Входные данные: a и b минимальное и максимальное значения интервала интегрирования, n – количество разбиений.
Выходные данные: I – решение.
120
