КП

Задание 1.

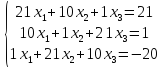
Метод Крамера.

∆=

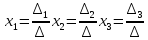
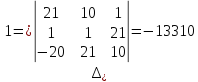
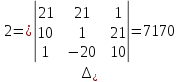
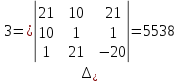
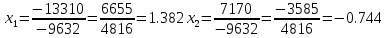
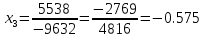
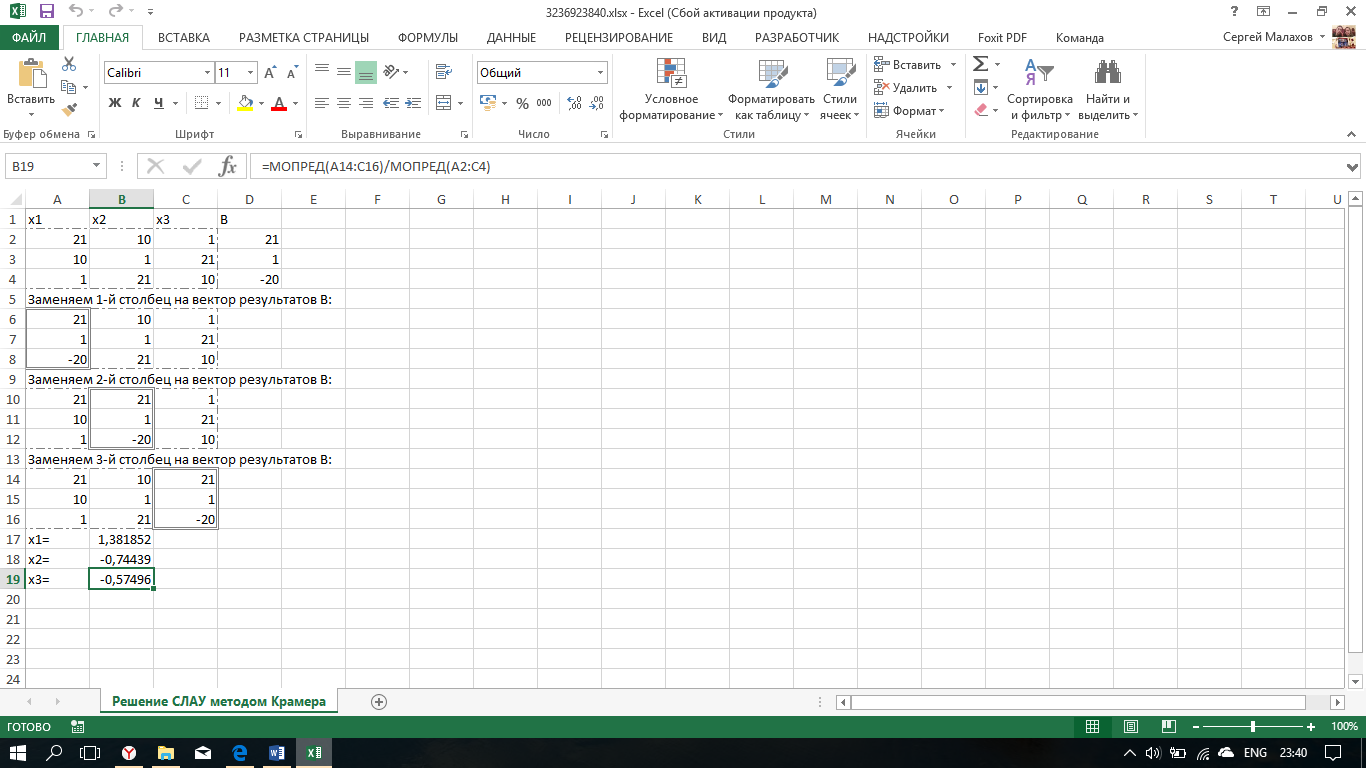
Метод Гаусса.

Нашёл единицу в 1-ом столбце и поменял местами 3-ю и 1-ую строки. Умножил 1-ю строку на 10.

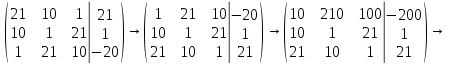
Вычел 1-ую строку из 2-ой строки и восстановил ее. Умножил 1-ую строку на 21.

Вычел 1-ую строку из 3-ей строки и восстановил ее. Получил единицу в 2-ом столбце разделив 2-ую строку на -209. Умножил 2-ую строку на 21.

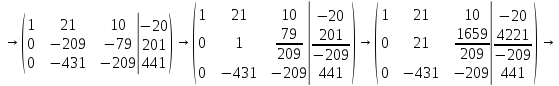
Вычел 2-ую строку из 1-ой строки и восстановил ее. Умножил 2-ую строку на -431. Вычел 2-ую строку из 3-ей строки и восстановил ее. Получил единицу в 3-ем столбце разделив 3-ю строку на -9632/209. Умножил 3-ю строку на 431/209

Вычел 3-ю строку из 1-ой строки и восстановил ее. Умножил 3-ю строку на 79/209.

Вычел 3-ю строку из 2-ой строки и восстановил ее.

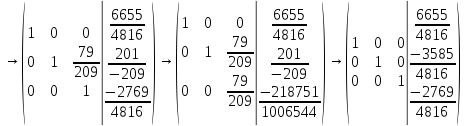
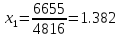
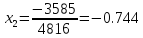
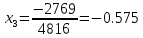
Метод обратной матрицы.

∆=

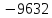
А=

В=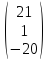

Х=А^-1*В

Для вычисления обратной матрицы найдем дополнительные миноры и алгебраические дополнения матрицы А.

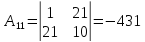
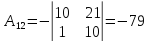
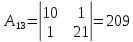
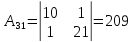
Транспонированная союзная матрица:

С^*Т=

А^-1=

=

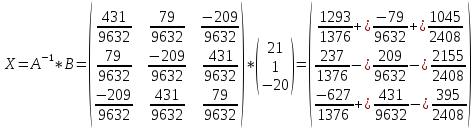
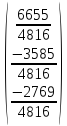
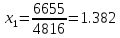
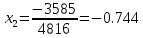
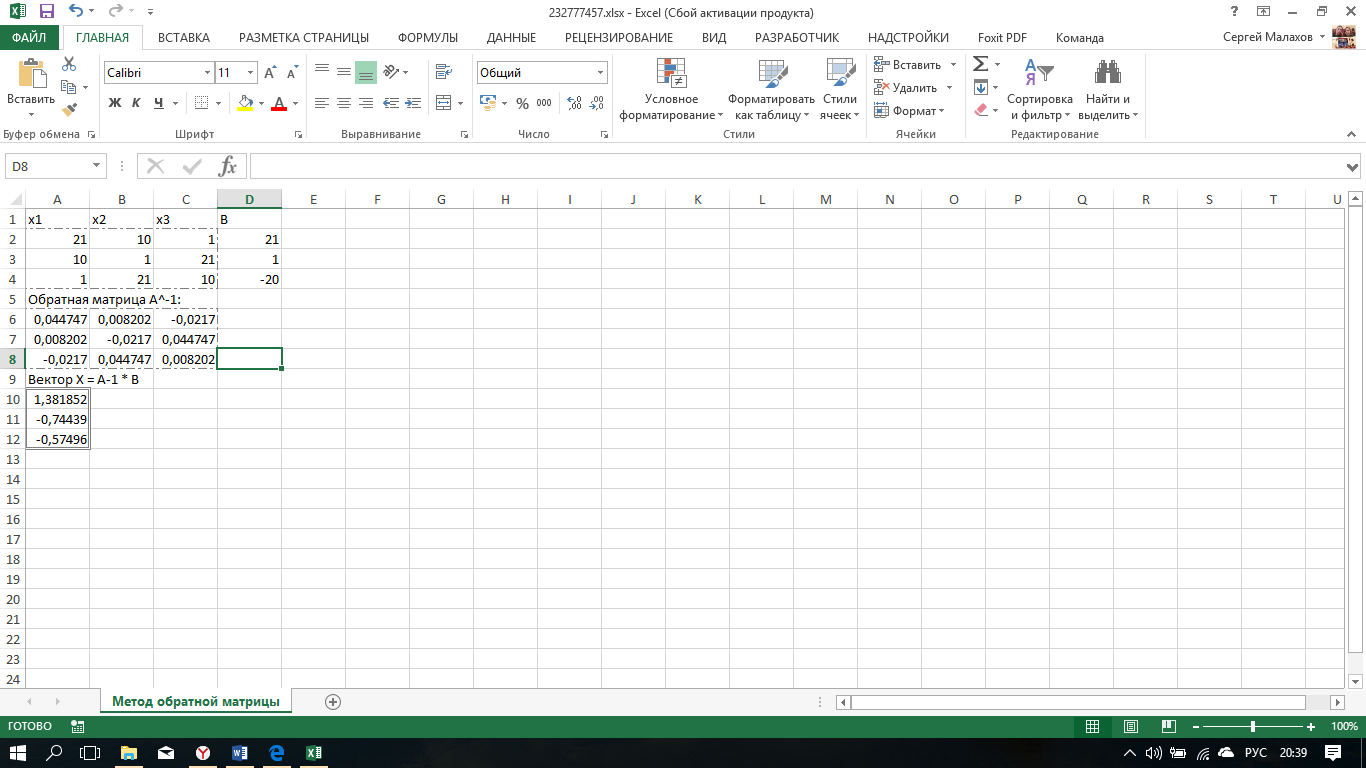
Метод LU-разложения.

A=B*C

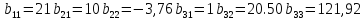
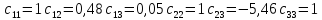
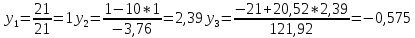
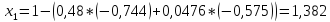
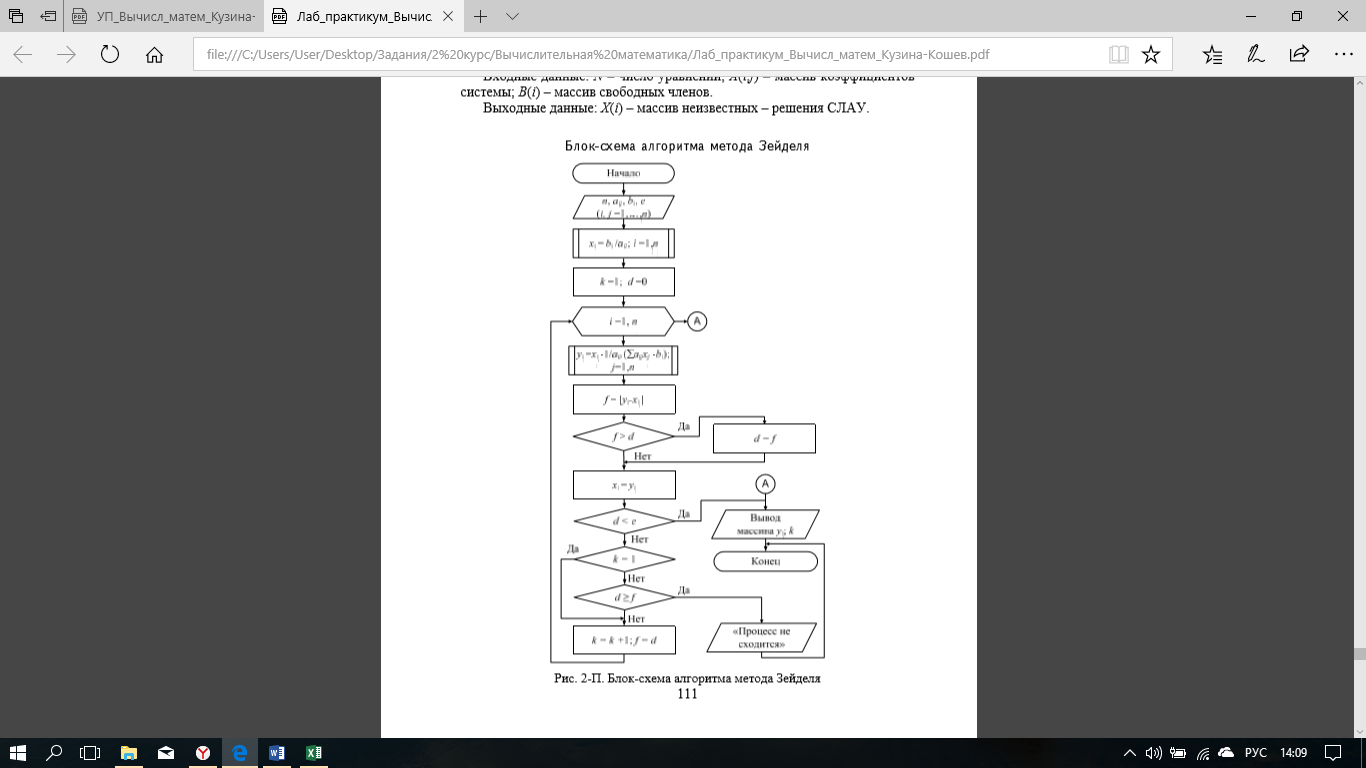
Блок-схемы:

Метод Крамера.

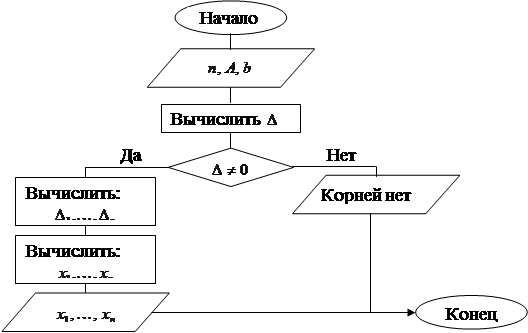
Метод Гаусса.

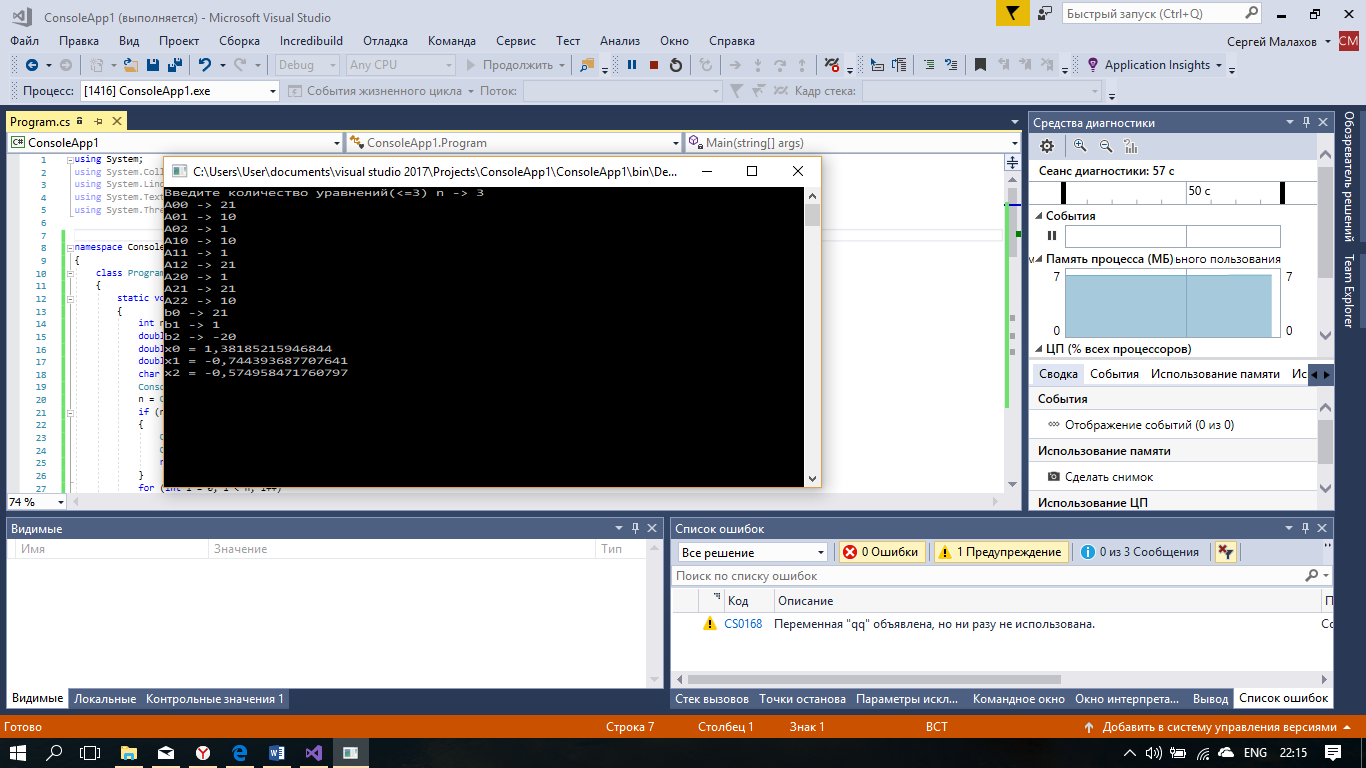
using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

namespace ConsoleApp1

{

class Program

{

static void Main(string[] args)

{

int n; /* количество уравнений */

double[,] A = new double[3, 3]; /* матрица системы */

double[] b = new double[3]; /* вектор правых частей */

double[] x = new double[3]; /* вектор решения */

Console.Write("Введите количество уравнений(<=3) n -> ");

n = Convert.ToInt32(Console.ReadLine());

if (n > 3 || n <= 1)

{

Console.WriteLine("Ошибка в размерности системы (n=2,3)");

Convert.ToInt32(Console.ReadLine());

return;

}

for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

{

Console.Write("A{0}{1} -> ", i, j);

A[i, j] = Convert.ToDouble(Console.ReadLine());

}

for (int i = 0; i < n; i++)

{

Console.Write("b{0} -> ", i);

b[i] = Convert.ToDouble(Console.ReadLine());

}

if (SLAU_kramer(n, A, b, x) == 1)

{

Console.WriteLine("Система не имеет решение");

Convert.ToInt32(Console.ReadLine());

return;

}

else

for (int i = 0; i < n; i++)

Console.WriteLine("x" + i + " = " + x[i]);

Console.ReadLine();

}

private

static double det(int n, double[,] B)

{

if (n == 2)

return B[0, 0] * B[1, 1] - B[0, 1] * B[1, 0];

return B[0, 0] * (B[1, 1] * B[2, 2] - B[1, 2] * B[2, 1]) - B[0, 1] * (B[1, 0] * B[2, 2] - B[1, 2] * B[2, 0]) +

B[0, 2] * (B[1, 0] * B[2, 1] - B[1, 1] * B[2, 0]);

}

static void equal(int n, double[,] A, double[,] B)

{

for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

A[i, j] = B[i, j];

}

static void change(int n, int N, double[,] A, double[] b)

{

for (int i = 0; i < n; i++)

A[i, N] = b[i];

}

public

static int SLAU_kramer(int n, double[,] A, double[] b, double[] x)

{

double[,] An = new double[3, 3];

double det1 = det(n, A);

if (det1 == 0) return 1;

for (int i = 0; i < n; i++)

{

equal(n, An, A);

change(n, i, An, b);

x[i] = det(n, An) / det1;

}

return 0;

}

}

}

Задание 2.

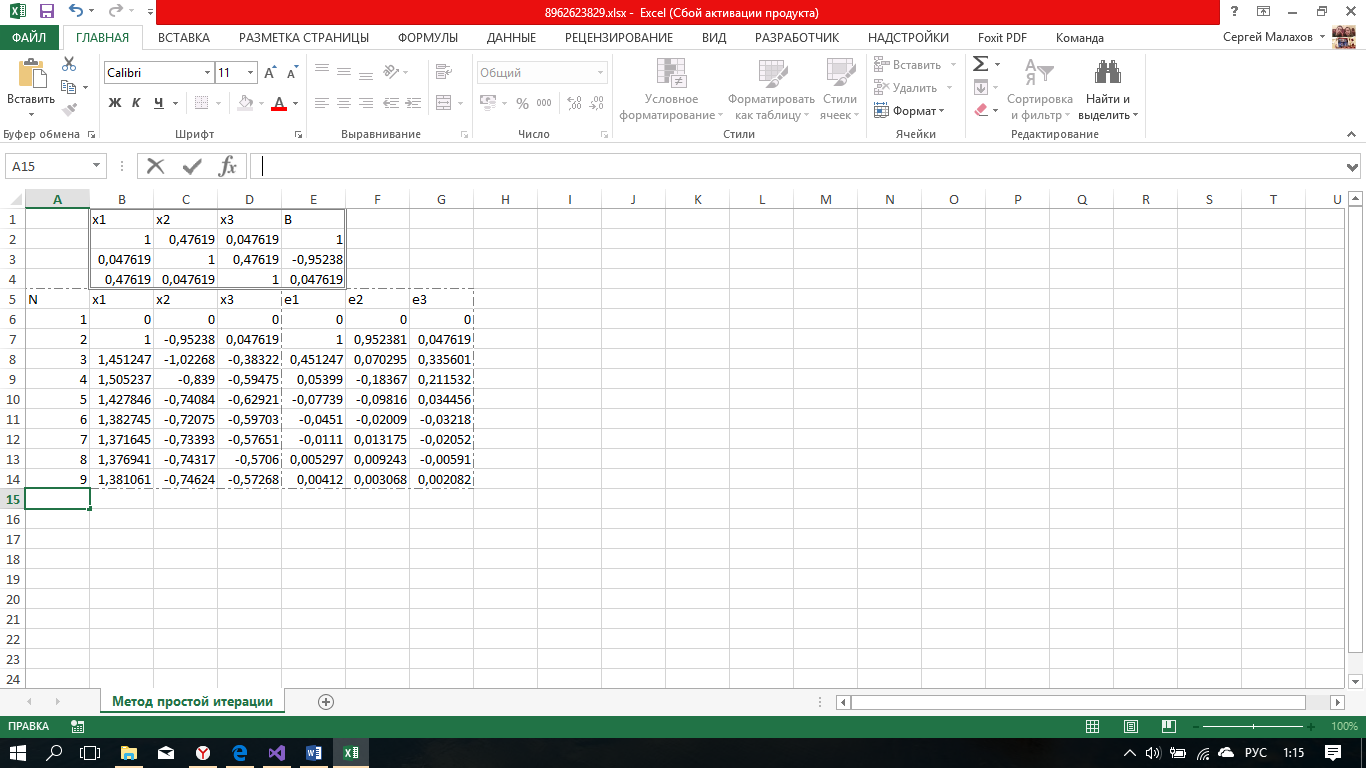
Метод простой иттерации.

Прежде чем применять метод итераций, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы. Если при этом условие все-таки не выполняется, то иногда удается обеспечить сходимость метода с помощью следующего метода.

x₁=β₁ -α₁₂x₂ -α₁₃x₃ -...-α_1nx_n x₂=β₂ -α₂₁x₁ -α₂₃x₃ -...-α_2nx_n x_n=β_n -α_n1x_n -α_n3x₃ -...-α_nn-1x_n-1 где βi=bi / aii; αij =aij/aii при i≠j; αii=0

Система (2) в матричной форме имеет вид:

x=β-αx

Пусть x0=β, тогда:

x1=b - a x0

x2=b - a x1

....

xk+1=b - a xk

Приведем к виду:

x1=1+0.48x2+0.0476x3

x2=-0.95238+0.0476x1+0.48x3

x3=0.0476+0.48x1+0.0476x2

Вычисления заканчиваются по критерию:

a = 0.47619+0.047619 = 0.5238

Покажем вычисления на примере нескольких итераций.

N=1

x1=1 - 0 • 0.47619 - 0 • 0.0476=1

x2=-0.95238 - 0 • 0.0476 - 0 • 0.47619=-0.95238

x3=0.0476 - 0 • 0.47619 - 0 • 0.0476=0.0476

N=2

x1=1 - (-0.95238) • 0.47619 - 0.0476 • 0.0476=1.45125

x2=-0.95238 - 1 • 0.0476 - 0.0476 • 0.47619=-1.02268

x3=0.0476 - 1 • 0.47619 - (-0.95238) • 0.0476=-0.38322

N=3

x1=1 - (-1.02268) • 0.47619 - (-0.38322) • 0.0476=1.50524

x2=-0.95238 - 1.45125 • 0.0476 - (-0.38322) • 0.47619=-0.839

x3=0.0476 - 1.45125 • 0.47619 - (-1.02268) • 0.0476=-0.59475

Остальные расчеты сведем в таблицу.

N	x1	x2	x3	e1	e2	e3
0	0	0	0
1	1	-0.952	0.0476	1	0.952	0.0476
2	1.451	-1.023	-0.383	0.451	0.0703	0.336
3	1.505	-0.839	-0.595	0.054	-0.184	0.212
4	1.428	-0.741	-0.629	-0.0774	-0.0982	0.0345
5	1.383	-0.721	-0.597	-0.0451	-0.0201	-0.0322
6	1.372	-0.734	-0.577	-0.0111	0.0132	-0.0205
7	1.377	-0.743	-0.571	0.0053	0.00924	-0.00591
8	1.381	-0.746	-0.573	0.00412	0.00307	0.00208
9	1.383	-0.745	-0.574	0.00156	-0.000795	0.00182
10	1.382	-0.745	-0.575	-0.000292	-0.00079	0.000781

Для оценки погрешности вычисляем коэффициент α:

mах[∑|αij|] = 0.47619+0.047619 = 0.52381<1

mах [|x9, x10|] = ρ (x9, x10) = |-0.57527 - (-0.57449) | = 0.00079

Вычисляем погрешность:

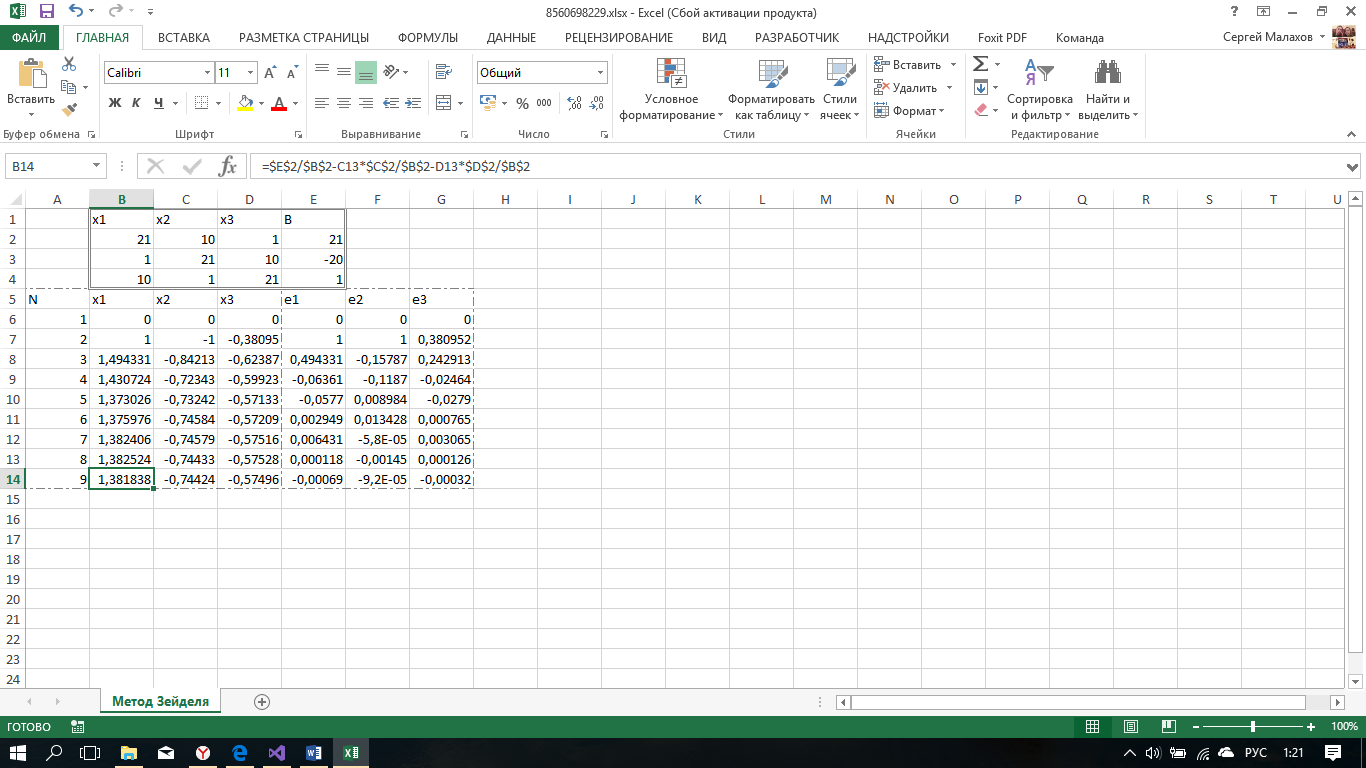
Метод Зейделя.

Имеем СЛАУ: Аx=b

Предполагая, что разрешим новое уравнение системы относительно х₁, второе – относительно х₂ и т.д. В результате получим:

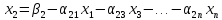
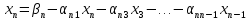
где , при

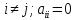
Известно начальное приближение: x⁰=(x⁰_1,….,x⁰_n).

Итерационная схема имеет вид:

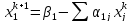
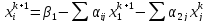Прежде чем применять метод, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы.

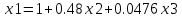
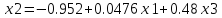
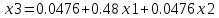
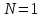
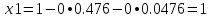
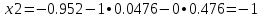
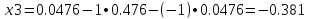
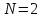
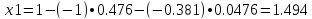
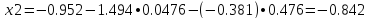
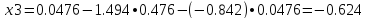
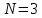
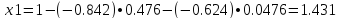
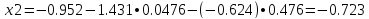
Остальные расчеты сведем в таблицу.

N	x1	x2	x3	e1	e2	e3
0	0	0	0
1	1	-1	-0.381	1	1	0.381
2	1.494	-0.842	-0.624	0.494	-0.158	0.243
3	1.431	-0.723	-0.599	-0.0636	-0.119	-0.0246
4	1.373	-0.732	-0.571	-0.0577	0.00898	-0.0279
5	1.376	-0.746	-0.572	0.00295	0.0134	0.000765
6	1.382	-0.746	-0.575	0.00643	-5.8E-5	0.00306
7	1.383	-0.744	-0.575	0.000118	-0.00145	0.000126
8	1.382	-0.744	-0.575	-0.000686	-9.2E-5	-0.000322

Для оценки погрешности вычисляем коэффициент α:

mах[∑|αij|] = 0.476+0.0476 = 0.524<1

mах [|x7, x8|] = ρ (x7, x8) = |-0.575 - (-0.575) | = 0.000686

Вычисляем погрешность:

namespace ConsoleApp2

{

class Program

{

static void Main(string[] args)

{

do

{

try

{

Console.WriteLine("Введите размер матрицы:");

int n = int.Parse(Console.ReadLine());

double[,] a = new double[n, n];

double[] b = new double[n];

double[] x = new double[n]; //нулевые приближения

for (int i = 0; i < n; i++)

{

x[i] = 0;

}

for (int i = 0; i < n; i++) //ввод матрицы

{

for (int j = 0; j < n; j++)

{

Console.WriteLine("Введите элемент [" + (i + 1) + "," + (j + 1) + "]:");

a[i, j] = double.Parse(Console.ReadLine());

}

}

for (int j = 0; j < n; j++) //ввод значений b

{

Console.WriteLine("Введите элемент [" + (j + 1) + "]:");

b[j] = double.Parse(Console.ReadLine());

}

Zeidel test = new Zeidel(a, b, 500, n, x);

bool IsDiagonal = test.DiagonallyDominant();

test.algoritm();

for (int j = 0; j < n; j++)

{

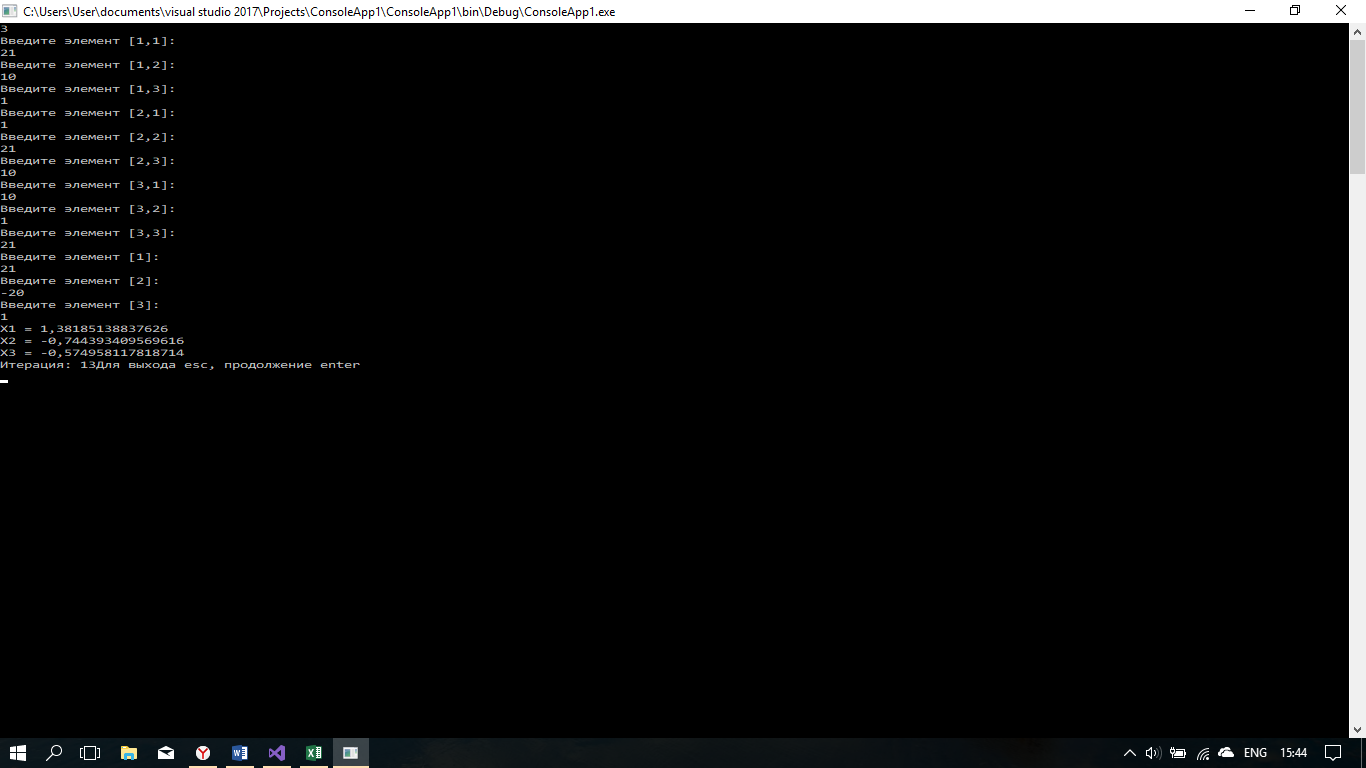
Console.WriteLine("X" + (j + 1) + " = " + test.roots[j]);

}

Console.WriteLine("Итерация: " + test.k + "Для выхода esc, продолжение enter");

}

catch (Exception ex)

{

Console.WriteLine(ex.ToString());

}

} while (Console.ReadKey().Key != ConsoleKey.Escape);

}

}

public class Zeidel

{

public static double epsilon = 0.000001; //точность вычисления

public int n, k, N; //N -допустимое число итераций, n - размерность квадратной матрицы коэффицентов, k-количество итераций

public double s, Xi, diff = 1; //s - сумма, величина погрешности

public double[,] matrix; //матрица коэффицентов

public double[] value; //матрица значений

public double[] roots; //матрица корней

public bool diagonal;

public Zeidel(double[,] matrix, double[] value, int N, int n, double[] roots)

{

this.matrix = matrix;

this.N = N;

this.value = value;

this.n = n;

this.roots = roots;

}

public bool DiagonallyDominant()

{

for (int i = 0; i < n; i++)

{

double sum = 0;

for (int j = 0; j < n; j++)

{

if (i != j)

{

sum += Math.Abs(matrix[i, j]);

}

}

if (Math.Abs(matrix[i, i]) >= sum)

{

diagonal = true;

break;

}

else

{

diagonal = false;

}

}

return diagonal;

}

public void algoritm()

{

k = 0;

while ((k <= N) && (diff >= epsilon))

{

k = k + 1;

for (int i = 0; i < n; i++)

{

s = 0;

for (int j = 0; j < n; j++)

{

if (i != j)

{

s += matrix[i, j] * roots[j];

}

}

Xi = (value[i] - s) / matrix[i, i];

diff = Math.Abs(Xi - roots[i]);

roots[i] = Xi;

}

}

}

}

}

Задание 3.

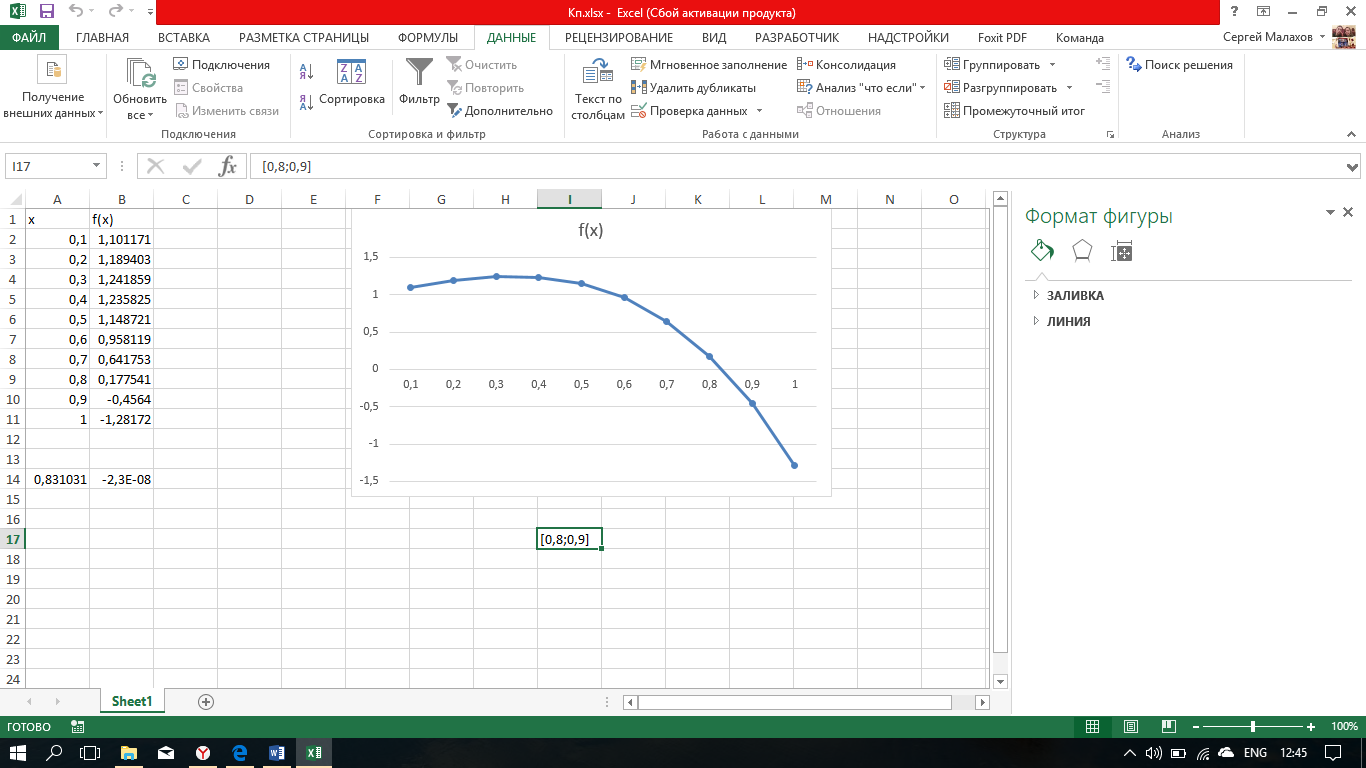
F(x)= e^x-4x³

ε = 0.0001

Метод половинного деления (метод дихотомии).

Число шагов, необходимых для достижения заданной точности определяется неравенством:

Поскольку F(0.8) *F(0.9) <0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0.8; 0.9].

N=1.

c = (0.8 + 0.9) /2 = 0.85

F(x) = -0.117

F(c) = 0.178

Поскольку F(c)•F(a) <0, то b=0.85

N=2.

c = (0.8 + 0.85) /2 = 0.825

F(x) = 0.0358

F(c) = -0.117

Поскольку F(c)•F(b) <0, то a=0.825

Остальные расчеты сведем в таблицу.

N	c	a	b	f(c)	f(x)	ε
1	0.85	0.85	0.9	0.1775	-0.1169	0.05
2	0.825	0.825	0.85	-0.1169	0.03582	0.025
3	0.8375	0.8375	0.85	0.03582	-0.03913	0.0125
4	0.8313	0.8313	0.8375	-0.03913	-0.00131	0.00625
5	0.8281	0.8281	0.8313	-0.00131	0.01734	0.00313
6	0.8297	0.8297	0.8313	0.01734	0.00804	0.00156
7	0.8305	0.8305	0.8313	0.00804	0.00337	0.000781
8	0.8309	0.8309	0.8313	0.00337	0.00103	0.000391
9	0.8311	0.8311	0.8313	0.00103	-0.000139	0.000195

Таким образом, в качестве корня можно принять:

x=(0.8309+0.8311) /2 = 0.831

Ответ: x = 0.831; F(x) = -0.000139.

Метод хорд.

Рассмотрим более быстрый способ нахождения корня на интервале [a, b], в предположении, что f(a)f(b) <0.

В точке x=x1, y=0, в результате получим первое приближение корня Проверяем условия:

1. f(x1) f(b) <0,

2. f(x1) f(a) <0.

Если выполняется условие (1), то в формуле точку a заменяем на x1, получим: Продолжая этот процесс, получим для n-го приближения: Пусть f(xi)f(a) <0. Записав уравнение хорды, мы на первом шаге итерационного процесса получим x1. Здесь выполняется f(x1) f(a) <0. Затем вводим b1=x1 (в формуле точку b заменяем на x1), получим:

Остановка процесса:

|xn – xn-1| <ε, ξ = xn.

Находим первую производную:

dF/dx = -12•x2+ex

Находим вторую производную:

d2F/dx2 = -24•x+ex

Поскольку F(0.8) *F(0.9) <0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0.8; 0.9].

Вычисляем значения функций в точке a = 0.8

f(0.8) = 0.178

f''(0.8) = -16.974

Поскольку f(a)•f''(a) <0, то x0 = b = 0.9

Остальные расчеты сведем в таблицу.

N	x	F(x)	h = F(x)*(b-x) /(f(b)-f(x))
1	0.8	0.1775	-0.02801
2	0.828	0.01805	-0.00274
3	0.8307	0.00172	-0.00026
4	0.831	0.000163	-0.000139

Ответ: x = 0.831; F(x) = -0.000139.

Метод Ньютона.

Поскольку F(0.8) *F(0.9) <0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0.8; 0.9].

Вычисляем значения функций в точке a = 0.8

f(0.8) = 0.178

f''(0.8) = -16.974

Критерий остановки итераций.

|f(xk)| <εm1

или где M2 = max|f "(x)|, m1 = min|f'(x)|.

Поскольку f(a)•f''(a) < 0, то x0 = b = 0.9

Остальные расчеты сведем в таблицу.

N	x	F(x)	dF(x)	h = f(x) / f'(x)
1	0.9	-0.4564	-7.2604	0.06286
2	0.8371	-0.03692	-6.0999	0.00605
3	0.8311	-0.000325	-5.9926	5.4E-5

Скорость сходимости метода Ньютона квадратичная с коэффициентом

α = M2/2m1, где M2 = max|f "(x)|, m1 = min|f'(x)|.

Ответ: x = 0.8311 - (-0.000325) / (-5.9926) = 0.83103146; F(x) = 0

Комбинированный метод.

Поскольку F(0.8) *F(0.9) <0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0.8; 0.9].

Вычисляем значения функций в точке a = 0.8

f(0.8) = 0.178

f''(0.8) = -16.974

Поскольку f(a)•f''(a) <0, то x0 = b = 0.9

Остальные расчеты сведем в таблицу.

N	x	F(x)	b	F(b)	h = f(b)*(b-x) /(f(b)-f(x))	hb = f(b)/f'(b)
1	0.8	0.1775	0.9	-0.4564	-0.02801	0.06286
2	0.828	0.01805	0.8371	-0.03692	-0.003	0.00605
3	0.831	0.000163	0.8311	-0.000325	-2.7E-5	5.4E-5