2.3. Содержание отчета

1. Структурные схемы и численные значения их параметров.

2. Результаты по каждому пункту программы работы и комментарии к ним. Ответы на вопросы, содержащиеся в программе работы.

3. Вычисление критических значений контурного коэффициента в заданиях 2.2.1 и 2.2.2 исходя из условия нахождения системы на границе устойчивости (по критерию Гурвица).

4. Графики зависимости и от . При определении учесть, что (Прокомментировать графики, изобразив по ПФ (см. начало программы работы) асимптотические ЛАХ разомкнутой системы при различных и (эскизно) ЛФХ.)

5. Значения корней стандартных полиномов и значения с анализом влияния на них значения и пояснением связи характера ПХ с картиной расположения корней на плоскости.

6. Эскиз диаграммы Вышнеградского с нанесенными на нее точками, определяющими заданные в таблице на с. 11 сочетания параметров и ; вывод о связи характера ПХ с полюсами ПФ.

Для построения диаграммы необходимо:

• изобразить систему координатных осей для параметров (ось абсцисс) и (ось ординат); оцифровку осей задать в пределах от 0 до 6;

• изобразить границу устойчивости согласно уравнению (выше этой границы располагается область устойчивости);

• для значений 0  A  3 изобразить кривую DC, описываемую уравнением ; правая граница этой кривой – точка C имеет координаты (3;3);

• изобразить кривые CE и CF (симметричные относительно биссектрисы квадранта), которые описываются одним и тем же параметрически заданным уравнением где – параметр; для построения кривой CE необходимо задавать (здесь ), а для построения кривой CF – 0  a  1 (здесь );

• обозначить цифрами I, II, и III следующие области:

I – между границей устойчивости и линией DCF (в этой области ХП имеет один вещественный корень и пару комплексно-сопряженных корней, расположенных ближе к мнимой оси, чем вещественный);

II – выше кривой DCE (здесь ХП имеет те же типы корней, что и в области I, но ближайшим к мнимой оси является вещественный корень);

III – между кривыми CF и CE (здесь все корни ХП вещественны).

2.4. Контрольные вопросы

1. Дайте определения основных показателей качества динамики САУ.

2. Как уменьшение запаса устойчивости отражается на значениях других показателей качества ?

3. Какими мерами можно повысить критическое значение контурного коэффициента усиления системы?

4. В чем польза диаграммы Вышнеградского?

5. Почему граница устойчивости на диаграмме описывается уравнением ?

6. Каковы значения корней ХП в точке C ?

Лабораторная работа № 3

Методы коррекции систем автоматического управления

Цель работы – изучение методов последовательной и параллельной коррекции САУ, типовых корректирующих устройств и их влияния на динамические свойства и точность систем.

3.1. Основные сведения

Синтез САУ, удовлетворяющей заданным требованиям к точности системы и качеству ее динамики, обычно проводят в два этапа:

1-й этап ­– проектирование основного регулятора, обеспечивающего заданную точность;

2-й этап – синтез специальных корректирующих устройств (КУ) для стабилизации системы, если она неустойчива, и(или) улучшения ее динамических свойств.

Среди КУ различают последовательные, включаемые в прямой канал системы, и параллельные, представляющие собой, как правило, различного рода обратные связи, чаще местные, т. е. охватывающие часть звеньев прямого канала. Достоинством таких КУ по сравнению с последовательными является то, что при правильном расчете (таком, чтобы в существенном диапазоне частот ЧПФ разомкнутого внутреннего контура была значительно больше единицы) ПФ внутреннего контура определяется в основном ПФ корректирующей обратной связи, вследствие чего вариации параметров звеньев, охваченных обратной связью, слабо влияют на динамику системы. Применяют также КУ, включаемые параллельно звеньям прямого канала.

Синтез САУ в частотной области обычно состоит в формировании желаемой ЛАХ разомкнутой системы с последующим расчетом корректирующего устройства, чаще параллельного, введение которого обеспечит эту ЛАХ. Однако в случае последовательной коррекции часто можно обойтись более простой процедурой введения в систему типовых КУ. Объединяя одним понятием "регулятор в прямом канале" основной регулятор и последовательное КУ, можно указать следующие типовые регуляторы, широко применяемые для улучшения динамики и повышения точности систем:

• П-регулятор: (при  1 увеличивает и уменьшает );

• И-регулятор: 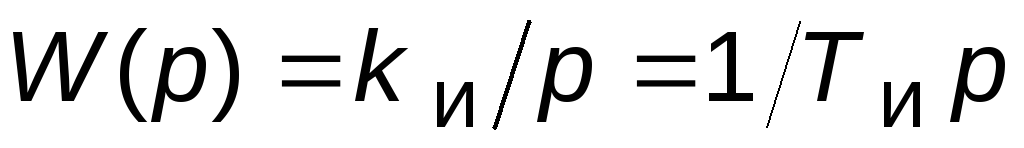(повышает порядок астатизма и уменьшает на );

• ПД-регулятор (форсирующее звено): (повышает ; реализуемая ПФ , где  );

• ПИ-регулятор: (обладает свойствами П-регулятора и первым из свойств И-регулятора);

• ПИД-регулятор: (сочетает свойства ПИ- и ПД-регуляторов; реально 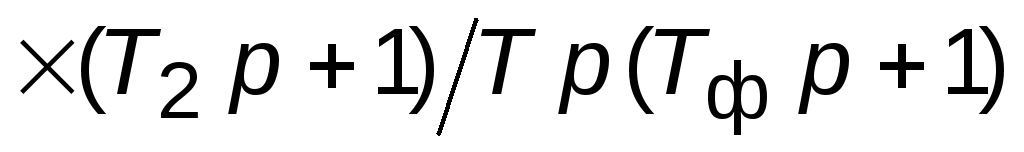, где – малая постоянная времени).

Некоторые способы определения порядка астатизма системы в отношении воздействия :

• представить ПФ для ошибки = E(p)/U(p) в виде где M(p) и N(p) – полиномы, причем ; тогда ;

• определить порядок астатизма как максимальное число не охваченных местными обратными связями интегрирующих звеньев в обратной связи системы с входом u и выходом e (ошибкой).