1. Индукция магнитного поля В.Закон Био-Савара-Лапласа. Сила Лоренца. Сила Ампера Если в данную точку магн. поля помещать рамки с различными магн. моментами, то на них действуют различные вращающие моменты, однако отношение М_max/р_m для всех контуров одно и то же и поэтому может служить харак-ой магнитного поля, назыв. Магн. индукцией: Магн. индукция в данной точке однородного магн. поля опр-ся макс. вращающим моментом, действующим на рамку с магн. момен­том =1, когда нормаль к рамке перпен-на направ-ию. поля. Связь между индукцией и напряженностью магн. Поля:

Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля dB, записывается в виде где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направ-ию с током, r—радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Модуль вектора dB: Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнит­ном поле, равна где dl—вектор, по модулю равный dl и совпадающий по направлению с током, В — вектор магнитной индукции. Модуль силы Ампера: . Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой где В — индукция магнитного поля, в котором заряд движется. Модуль силы Лоренца: . Направ-е силы Лоренца опред. с помощью правила левой руки.

2.Теорема о циркуляции вектора В и ее применения. Поле соленоида и тороида. Поток вектора магнитной индукции. З-н полн. тока для магн. поля в вакууме (теорема о циркуляции вектора В): цирк-ия вектора В по произвольн. замкн. контуру равна произведению магн. постоянной ₀ на алгебраич. сумму токов, охватываемых этим кон­туром: где n — число проводников с токами, охват-мых контуром L произвол. формы.

П отоком вектора магнитной индукции (магнитным потоком) через площадку dS называ­ется скалярная физич. величина, равная где B_n=Вcos—проекция вектора В на направление нормали к площадке dS (— угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направ.его совпадает с направ. нормали n к площадке. В может быть как полож., так и отриц. в зависимости от знака cos. Ф_B через произвольную поверхность S равен Для однородного поля и плоской поверх-и, располож. перпенд-о вектору В, B_n=B=const и Единица - вебер (Вб). Внутри соленоида поле является однородным, вне соленоида — неоднородным и оч. слабым. Магн. индукции поля внутри соленоида (в вакууме): Магн. поле, сосредоточено внутри тороида, вне его поле отсутствует, магн. индукция:

3.Электромагнитная индукция. Закон Фарадея. Правило Ленца. Самоиндукция.Взаимоиндукция. Явление электромаг­нитной индукции заключ. в том, что в замкн. проводящем контуре при изменении потока магн. индукции, охват-мого этим контуром, возникает электрич. ток, получив. название индукционного. З.н электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магн. индукции, охват-мого замкн. проводящим кон­туром, возник-ая в контуре э. д. с. Знак минус показывает, что увеличение потока вызывает э. д. с. т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока вызывает т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле определяется правилом Ленца. Правило Ленца: индукционный ток в контуре имеет всегда такое направ., что создав-ое им магн. поле препятствует изменению магн. потока, вызва­вшему этот индукц-ый ток.

При изменении силы тока в контуре будет изменяться также и сцепленный с ним магн.поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. (Гн): э. д. с. самоиндукции Явление возник-ия э.д.с. в одном из контуров при изменении силы тока в другом назыв. взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Взаимная индуктивность двух катушек, намотанных на общий тороидальный сердечник,

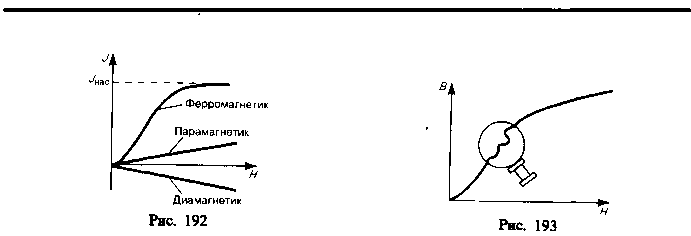
4. Магнитное поле в.Веществе. Диа-, пара- магнетизм. Вектор намагниченности.

Парамагнетики — вещ-ва, которые намагнич. во внеш. магн. поле в направ. внеш. магн. поля (J↑↑H) и имеют полож. магн. восприимчивость. Парамагнетики относятся к слабомагнитным вещ-ам, магнитная проницаемость Диамагне́тики — вещ-ва, намагнич-ся против направ. внеш. магн. поля. В отсутствие внеш. магн. поля диамагнетики не магнитны. Магнитная проницаемость и слабо зависит как от напряжённости магнитного поля, так и от температуры. Для колич-го описания намагничения магнетиков вводят вектор. величину — намагниченность, определяемую магн. моментом единицы объема магнетика: где — магн. момент магнетика, представ-ий собой вектор. сумму магн. моментов отдельных молекул. С другой стороны, I'/l — ток, приходящийся на единицу длины цилиндра, или его лин. плотность, поэтому магн. момент этого тока p = I'lS/l = I'V/l, где V — объем магнетика. Если Р — магн. момент магнетика объемом V, то намаг­нич. магнетика В несильных полях намагнич. прямо пропорц. напряженности поля, вызывающего намагничение, т. е.

5.Закон полного тока для магнитного поля в веществе.

З-н полного тока для магн. поля в вещ-ве (теорема о циркуляции вектора В) является: где I и I' — соответственно алгебраич. суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охват-мых произв-ым замкн. кон­туром L. Таким образом, циркуляция вектора магн. индукции В по произв-му замкн. контуру равна алгебраич. сумме токов проводимости и молеку­лярных токов, охватываемых этим контуром, умнож. на магнитную постоянную. Вектор В харак-ет результирующее поле, созданное как мак­роскопич.токами в проводниках (токами проводимости), так и микроскопич. токами в магнетиках, поэтому линии вектора магн.индукции В не имеют источников и являются замкнутыми.Циркуляция намагниченности J по произв. Замк. контуру:

Тогда закон полного тока для магнитного поля в вещ-ве

6.Ферромагнетики.Ферромагнетики — вещ-ва, облад. спонтанной намагниченностью, т. е. они намагниче­ны даже при отсутствии внеш. магн. поля. К ферромагнетикам кроме железа от­носятся, кобальт, никель, гадолиний, их сплавы и соединения. По мере возрастания Н намагниченность J сначала растет быстро, затем медленнее и, наконец, достигается так называемое магнитное насыщение J_нас, уже не завис. от напряженности поля. Сущест. особенность ферромагнетиков — не только большие значения  (для железа — 5000, для сплава супермаллоя — 800 000!), но и зависимость  от Н .Вначале  растет с увеличением Н, затем, достигая максимума, начинает уменьшаться, стремясь в случае сильных полей к 1 (= B/(₀H) = 1 + J/H, поэтому при J = J_нас = const с ростом Н отношение J/H 0,1). Зависимость J от H (а следовательно, и В от Н) определяется предысторией намагниче­ния ферромагнетика. Это явление получило название магнитного гистерезиса. При действии на ферромагнетик переменного магнитного поля намагниченность J изменяется в соответствии с кривой 1—2—3—4—5—6—1, которая называется петлей гистерезиса. Для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. Процесс намагничения ферромагнетиков сопровождается изменением его линейных размеров и объема. Это явление получило название магнитострикции.