6. Кинетическая энергия вращения.

гдеJ_z —момент инерции тела относительно оси z. Таким образом,Кинетическая энергия вращающегося телаВ случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:гдеm— масса катящегося тела;v_c —скорость центра масс тела;Jc —момент инер­ции тела относительно оси, проходящей через его центр масс;— угловая скорость тела.

7. Момент сил. Основное уравнение динамики вращательного движения.

Моментом силы F относительно неподвижной точкиОназывается физическая величина, определяемая векторным произведением радиуса-вектораr, проведенного из точ­киОв точкуАприложения силы, на силуF(рис. 25):

Здесь М — псевдовектор,его направление совпадает с направлением поступательного движения правого винта при его вращении отrк F. Модуль момента силы

где — угол междуrиF;rsin=l— кратчайшее расстояние между линией действия силы и точкойО — плечо силы.

Моментом силы относительно неподвижной осиzназываетсяскалярнаявеличинаM_z , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точкиОданной осиz(рис. 26). Значение моментаМ_zне зависит от выбора положения точкиОна оси z.

Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

Уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Можно показать, что если ось zсовпадает с главной осью инерции проходящей через центр масс, то имеет место векторное равенство

где J —главный момент инерции тела (момент инерции относительно главной оси).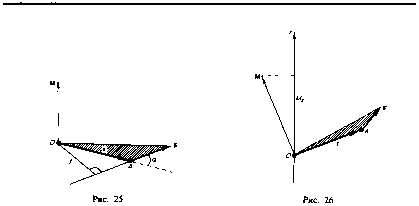

8. Момент импульса. Закон сохранения момента импульса.

Моментом импульса (количества движения) материальной точкиА относительно неподвижной точки О называется физическая величина, определяемая векторным произ­ведением:

где r— радиус-вектор, проведенный из точки О в точкуA, p=mv —импульс мате­риальной точки (рис. 28);L—псевдовектор,его направление совпадает с направлением поступательного движения правого винта при его вращении отrк р.

Модуль вектора момента импульса

где  —угол между векторами r и р, l— плечо вектораротносительно точкиО.

Моментом импульса относительно неподвижной осиzназывается скалярная величинаL_z,равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точкиОданной оси. Момент импульсаL_zне зависит от положения точкиОна осиz.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:или

В замкнутой системе момент внешних сил откуда

Выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. Закон сохранения момента импульса —фундаментальный закон природы.

9.Гармонические колебания. Физический и математический маятник. Пружинный маятник.

Колебанияминазываются движения или процессы, которые характеризуются опреде­ленной повторяемостью во времени.Гармонические колебания —колебания, при которых колеб­лющаяся величина изменяется со временем по закону синуса (косинуса).периодические процессы(процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колеба­ния величиныsописываются уравнением типагдеА —максимальное значение колеблющейся величины, называемое амплитудой колебания,₀— круговая (циклическая) частота, — начальная фаза колебанияв мо­мент времениt=0, (₀t+) —фаза колебанияв момент времениt. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, тоsможет принимать значения от+Адо–А.

Пружинный маятник совершает гармоничес­кие колебания с циклической частотойи периодомПотенциальная энергия равнаУравнение движения маятникаФизический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точкуО, не совпадающую с центром массСтела. Период колебаний:гдеL=J/(ml) —приведенная длина фи. Математический маятник— этоидеализированнаясистема, состоящая из материальной точки массойт,подвешенной на нерастяжимой невесомой нити, и колеб­лющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятникагдеl— длина маятника, выражение для периода малых колебаний