5.6. Системы осей координат

   При определении сил и моментов, действующих на самолет в полете, при исследовании траекторий движения самолета, при решении многих других вопросов в процессе проектирования используют несколько прямоугольных (ортогональных) декартовых правых систем осей координат.

Рис. 5.27. Нормальная земная система осей координат	Рис. 5.28. Связанная система осей координат

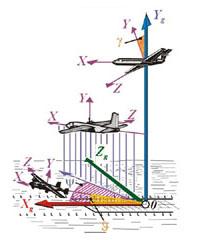
   Положение самолета относительно Земли определяется углами между осями связанной (0XYZ) и нормальной земной (0X_gY_gZ_g) системами осей координат.

Рис. 5.29. Положение самолета относительно Земли

Рис. 5.30. Положение самолета относительно вектора скорости

Взаимно перпендикулярные оси нормальной земной системы осей координат (рис. 5.27) 0X_g и 0Z_g лежат на поверхности Земли, ось 0Y_g направлена по местной вертикали вверх. Начало системы координат и направление осей 0X_g и 0Z_g выбираются в соответствии с решаемой задачей. Так, при исследовании траекторий взлета самолета оказывается удобно поместить начало координат в точке старта самолета, а горизонтальную ось 0X_g совместить с осью ВПП.    Начало0 связанной системы осей координат (рис. 5.28) помещено в центр масс (ц. м.) самолета, ось 0X направлена от хвостовой к носовой части самолета, ось 0Y перпендикулярна оси 0X и направлена вверх в плоскости симметрии, ось 0Z перпендикулярна плоскости симметрии самолета и направлена в сторону правой консоли крыла.    Таким образом, положение самолета относительно Земли определяется (рис. 5.29) углом тангажа , углом крена  и углом рыскания .    В общем случае движения самолета в пространстве вектор скорости самолета (или, в соответствии с законом обратимости движения, вектор скорости набегающего потока) не совпадает со связанной продольной осью самолета 0X.    Положение самолета относительно вектора скорости определяется углами между осями связанной (0XYZ) и скоростной (0X_aY_aZ_a) систем осей координат.    Начало 0 скоростной системы (рис. 5.30) осей координат помещено в центр масс самолета, ось 0X_a совпадает по направлению с вектором скорости самолета, ось 0Y_a направлена к верхней части самолета в плоскости его симметрии, ось 0Z_a перпендикулярна плоскости 0X_aY_a.
Положение самолета относительно вектора скорости набегающего потока определяетсяуглом атаки  и углом скольжения .

5.7. Аэродинамические характеристики самолета

   В общем случае при полете самолета (при наличии угла атаки α и угла скольжения β) вектор полной аэродинамической силы самолета R_a ориентирован в пространстве произвольным образом. В соответствии с записанным ранее выражением для полной аэродинамической силы проекции ее на оси скоростной системы координат можно записать в следующем виде:

Здесь Y_a - подъемная сила самолета, Н; X_a - сила лобового сопротивления (составляющая силы R_a по оси OX_a скоростной системы осей координат, взятая с обратным знаком), Н; Z_a - боковая сила, Н; C_Ya, C_Xa , C_Za - соответственно безразмерные коэффициенты подъемной силы, силы лобового сопротивления и боковой силы; S - площадь крыла самолета, м²; ρV²/2 - скоростной напор, Па.    Отсюда

   Физический смысл коэффициентов C_Ya, C_Xa, C_Za аналогичен физическому смыслу коэффициента полной аэродинамической силы C_Ra .    Составляющие ( C_Ya, C_Xa и C_Za ) безразмерного коэффициента полной аэродинамической силы C_Ra и положение точки ее приложения (центр давления) полностью описывают аэродинамические характеристики самолета.    В установившемся полете без скольжения (β=0) боковая сила отсутствует, поэтому, естественно,

Обычно принято представлять аэродинамические характеристики самолета в виде зависимостей составляющих коэффициента полной аэродинамической силы ( C_Ya и C_Xa ) от полетных углов (α и β). Примерные зависимости C_Ya(α) и C_Xa (α) приведены на рис. 5.31.

Рис. 5.31. Зависимость аэродинамических коэффициентов от угла атаки (пример)

Рис. 5.32. Поляра самолета (пример)

При достижении критического угла атаки на крыле начинается срыв потока, подъемная сила резко падает. Срыв обычно начинается не одновременно на левой и правой консоли крыла (франц.console - конструкция, жестко закрепленная одним концом при свободном другом).
Это происходит вследствие наличия скольжения, технологических неточностей при изготовлении самолета - возможна"валежка" (резкое кренение самолета). Поэтому в эксплуатации ограничивают диапазон летных углов атаки самолета предельно допустимым углом α_доп, который меньше α_кр на 2-5°.
Одной из форм представления аэродинамических характеристик самолета являетсяполяра - взаимозависимость коэффициентов C_Ya и C_Xa (рис. 5.32). Каждая точка на поляре соответствует определенному углу атаки α.
Обычно при построении поляры принято масштаб дляC_Ya брать крупнее, чем для C_Xa.
Если построить поляру в одинаковых масштабах дляC_Ya и C_Xa (рис. 5.33), то ее можно рассматривать как полярную диаграмму в координатах C_Ra и φ, где φ - угол наклона полной аэродинамической силы к направлению потока V_. В этом случае поляра является геометрическим местом концов вектора коэффициента полной аэродинамической силы C_Ra. Характерными точками поляры являются:

Рис. 5.33. К объяснению сущности поляры Начало формы Конец формы

-угол α_о нулевой подъемной силы (C_Ya=0; C_Xa= C_Xa0 C_Xamin );
-наивыгоднейший угол атаки α_нв, соответствующий максимальному аэродинамическому качеству самолета, определенному нами ранее как отношение подъемной силы самолета к силе лобового сопротивления.
При фиксированном угле атакиαi, соответствующем определенному режиму полета, K_a = Y_a/X_a=C_Ya/C_Xa, т. е. аэродинамическое качество определяется безразмерными коэффициентами аэродинамических сил, учитывающими форму обтекаемого тела, состояние его поверхности и его положение относительно набегающего потока воздуха при заданной скорости полета (M=const). Из рис. 5.33 видно, что аэродинамическое качество определяется как

K_a=Y_a / X_a=tgφ

Максимальному качеству K_a max будет соответствовать угол атаки aнв, полученный как точка касания поляры с прямой, проведенной из начала координат.    Критическому углу атаки α_кр соответствует максимальный коэффициент подъемной силы C_Ya max.    Углу атаки α_доп соответствует предельно допустимый коэффициент подъемной силы C_Ya доп.    Ранее отмечалось, что сила индуктивного сопротивления X_{a i} ~ Y_a², соответственно коэффициент индуктивного сопротивления запишем в виде C_{Xa i}=AC_Ya², где коэффициент A, характеризующий сопротивление, обусловленное подъемной силой, учитывает влияние формы крыла самолета на скос потока. Естественно, что, чем длиннее крыло, тем меньше будет влияние перетекания потока с нижней поверхности крыла на верхнюю, тем меньше будет скос потока и меньше C_{Xa i}.    Принимая во внимание выражение C_Xa=AC_Ya ² , в диапазоне летных углов атаки можно аппроксимировать поляру самолета квадратичной параболой

C_Xa=C_Xa0 + A C_Ya²

Коэффициент A называют иногда коэффициентом отвала поляры или просто отвалом поляры.

Рис. 5.34. Зависимость аэродинамического качества от угла атаки (пример)

На основании поляры самолета можно построить зависимость аэродинамического качества от угла атаки (рис. 5.34).
Значения аэродинамических коэффициентов существенным образом зависят от скорости (числаМ) полета. Для скоростей полета, соответствующих M_< M_крит, коэффициент лобового сопротивления C_Xaо определяется только силами сопротивления трения и сопротивления давления. Для скоростей полета, соответствующих M_M_крит, к этому сопротивлению добавляется волновое сопротивление.
В общем виде

C_Xaо=C_Xa тр _тр + C_Xa д _д + C_{Xa в}

где	CXa тр	-	коэффициент лобового сопротивления сил трения;
	CXa д	-	коэффициент лобового сопротивления сил давления;
	CXa в	-	коэффициент волнового сопротивления.

Следовательно, все аэродинамические характеристики самолета должны быть известны не только в диапазоне летных углов атаки, но и во всем диапазоне скоростей (чисел М) полета.    Примерная зависимость аэродинамических коэффициентов для прямого крыла от числа М приведена на рис. 5.35. Здесь коэффициент C ^α_Ya - производная коэффициента подъемной силы C_Ya по углу атаки α, 1/рад; C ^α_Ya=C_Ya/(α - α_о) (см. рис. 5.31).

Рис. 5.35. Зависимость аэродинамических коэффициентов прямого крыла от числа М (пример)

До чиселМ  0,4 значения всех аэродинамических коэффициентов практически постоянны, так как сжимаемость воздуха в потоке не проявляется.
С ростом скорости до соответствующейM_крит увеличение коэффициента C ^α_Ya происходит из-за проявления сжимаемости и увеличения зоны разрежения над крылом; коэффициент C_Xaо медленно растет из-за увеличения зоны повышенного давления перед крылом.
В диапазоне чиселМ от M_крит до М=1 увеличение C ^α_Ya замедляется из-за образования местной сверхзвуковой зоны и прямого скачка уплотнения над крылом и достигает максимума к моменту появления местной сверхзвуковой зоны и скачка уплотнения под крылом. С дальнейшим ростом скорости происходит сначала уменьшение до минимума, а затем опять увеличение коэффициента C ^α_Ya, так как смещаются к задней кромке скачки уплотнения сначала на нижней, а затем на верхней поверхности крыла, что сопровождается соответствующим увеличением зон разрежения на этих поверхностях. Увеличение коэффициента C ^α_Ya прекращается с появлением головного прямого отсоединенного скачка при М=1.
Одновременно резко увеличивается коэффициент лобового сопротивления в связи с развитием волнового кризиса; коэффициентC_Xaо достигает максимального значения при М=1 вследствие появления головного прямого отсоединенного скачка.
В диапазоне чиселM>1 с ростом сверхзвуковой скорости головной скачок уплотнения приближается к передней кромке, приобретая форму косого, затем скачок становится присоединенным, углы наклона скачков уменьшаются, соответственно уменьшаются зоны возмущений на верхней и нижней поверхностях профиля, что приводит к уменьшению коэффициентов C ^α_Ya и C_Xaо.
Резкое увеличение лобового сопротивления (рис. 5.35, 5.36) и, соответственно, уменьшение качества самолета (рис. 5.37) требуют для полета со скоростями, соответствующимиM >M_крит (преодоления так называемого "звукового барьера"), значительного увеличения тяги двигателя P.
Напомним, что для совершения горизонтального полета необходимо выполнить условия:

   Отсюда потребная для горизонтального полета тяга двигателя

   Самолеты с прямым крылом и поршневыми двигателями с воздушными винтами не могли не только достигнуть скоростей полета, соответствующих M 1, но даже и приблизиться к таким скоростям.

Рис. 5.36. Зависимость максимального аэродинамического качества от числа М и конфигурации крыла самолета (пример)	Рис. 5.37. Зависимость коэффициента лобового сопротивления от числа М и конфигурации самолета (пример)

   Рис. 5.36 и 5.37 достаточно наглядно показывают, что выбор соответствующих форм самолета позволяет существенным образом снизить неблагоприятное влияние сжимаемости при полете на высоких скоростях.    Приблизиться к "звуковому барьеру", а затем и преодолеть его стало возможным в связи с созданием реактивных двигателей и разработкой аэродинамиками и конструкторами новых форм самолета.