7. Математическое ожидание и его свойства. Вычисление математического ожидания по выбору

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Пусть случайная величина Х может принимать только значения х_1, х₂ … х_n, вероятности которых соответственно равны p_1, p_2, … p_n. Тогда математическое ожидание М (Х) случайной величины Х определяется равенством: 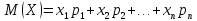. Если дискретная случайная величина Х принимает счетное множество возможных значений, то 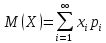, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С. ДОКАЗАТЕЛЬСТВО: будем рассматривать постоянную С как дискретную случайную величину, которая имеет одно возможное значение С и принимает его с вероятностью p=1. Следовательно, M(C)=C1=C

2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х). ДОКАЗАТЕЛЬСТВО: пусть случайная величина Х задана законом распределения вероятностей: Х х₁ х₂… х_n

P p₁ p₂ … p_n

Напишем закон распределения случайной величины СХ: CX Cx₁ Cx₂ … Cx_n

P p₁ p₂ … p_n

Математическое ожидание случайной величины СХ:

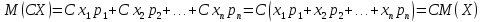
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)M(Y). ДОКАЗАТЕЛЬСТВО: пусть независимые случайные величины X и Y заданы своими законами распределения вероятностей: X х₁х₂ Y y₁y₂

P p₁p₂ g g₁g₂

Составим все значения, которые может принимать случайная величина X. Для этого перемножим все возможные значения Х на каждое возможное значение Y; в итоге получим 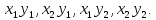Напишем закон распределения ХУ, предполагая, что все возможные значения произведения различны: XY

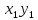
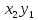
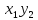
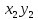
p

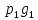
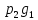
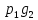
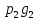
Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:

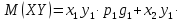
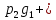
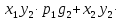
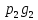
СЛЕДСТВИЕ: математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y)=M(X)+M(Y). СЛЕДСТВИЕ: математическое ожидание сумм нескольких случайных величин равно сумме математических ожиданий слагаемых.

8. Дисперсия случайной величины и ее свойства.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: .

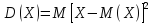Свойства дисперсии:

1. Дисперсия постоянной величины С равна нулю: D(C)=0. ДОКАЗАТЕЛЬСТВО: по определению дисперсии, 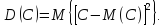Пользуясь первым свойством мат ожидания (мат ожидание постоянной равно самой постоянной), получим

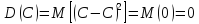
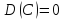
Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 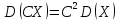. ДОКАЗАТЕЛЬСТВО: по определению дисперсии имеем 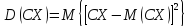. Пользуясь вторым свойством мат ожидания (постоянный множитель можно выносить за знак мат ожидания), получим

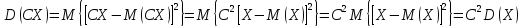
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: 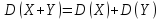. ДОКАЗАТЕЛЬСТВО: по формуле для вычисления дисперсии имеем 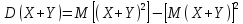. Раскрыв скобки и пользуясь свойствами мат ожидания суммы нескольких величин и произведения двух независимых случайных величин, получим

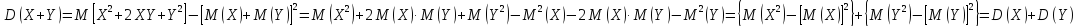
СЛЕДСТВИЕ 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

СЛЕДСТВИЕ 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины D(C+X)=D(X). ДОКАЗАТЕЛЬСТВО: величины С и Х независимы, поэтому, по 3-у свойству, D(C+X)=D(C)+D(X). В силу первого свойства D(C)=0. Следовательно, D(C+X)=D(X).

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X-Y)=D(X)+D(Y). ДОКАЗАТЕЛЬСТВО: в силу 3-го свойства D(X-Y)=D(X)+D(-Y). По 2-у свойству D(X-Y)=D(X)+(-1)²D(Y)