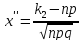3.Условная вероятность. Формула полной вероятности. Формула Бейеса.

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной.

Условной вероятностью 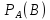 называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна 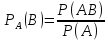(P(A)›0)

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события А равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

.

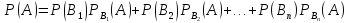Эта формула называется формулой полной вероятности.

ДОКАЗАТЕЛЬСТВО: по условию, событие А может наступить, если наступит одно из несовместных событий В₁, В₂, …,B_n. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В₁А, В₂А, …, B_nА. Пользуясь для вычисления события А теоремой сложения, получим

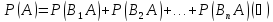
Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем

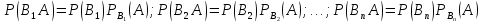
Подставив первые части этих равенств в соотношение 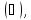получим формулу полной вероятности

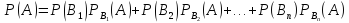
Пусть событие А может наступить при условии появления одного из несовместных событий В₁, В₂, …,B_n, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности

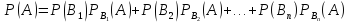
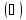
Допустим, что произведено испытание, в результате которого появилось событие А. Будем искать условные вероятности

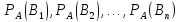
Найдем сначала условную вероятность 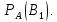По теореме умножения имеем

Заменив здесь Р(А) по формуле 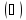, получим

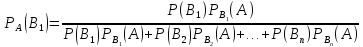
4. Повторные независимые испытания. Формула Бернулли. Локальная и интегральная теорема Лапласа.

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность.

Сложное событие – это совмещение нескольких отдельных событий, которые называют простыми.

Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна p^kq^n-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. 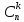. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженного на их число:

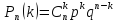
или

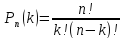
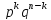
Полученную формулу называют формулой Бернулли.

ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА: если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятностью Р_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (чем точнее, тем больше n) значению функции

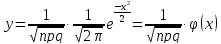
при 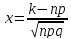. Имеются таблицы, в которых помещены значения функции 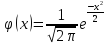, соответствующее положительным значениям аргумента х. для отрицательных значений аргумента пользуются теми же таблицами, т.к. функция 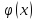четна, т.е. .

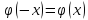Вероятность того, что событие А появится в n независимых испытаниях ровно k раз, приблизительно равна 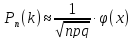, при .

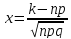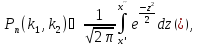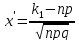ИНТЕГРАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА: если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность где и

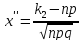
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, т.к. неопределенный интеграл не выражается через элементарные функции. Функцию Ф(х) часто называют функцией Лапласа. Для того, чтобы можно было пользоваться таблицей функции Лапласа, преобразуем отношение 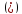так:

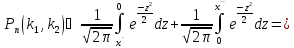
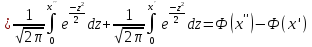
Вероятность того, что событие А появится в n независимых испытаниях от k₁ до k₂ раз,

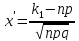, где и