
- •Предмет теории вероятности. Случайные события. Пространство элементарных событий. Операции над событиями.
- •Классическое определение вероятности. Теорема сложения несовместных событий. Геометрические вероятности.
- •3.Условная вероятность. Формула полной вероятности. Формула Бейеса.
- •Повторные независимые испытания. Формула Бернулли. Локальная и интегральная теорема Лапласа.
- •Определение дискретной случайной величины. Закон распределения случайной величины. Биноминальная и Пуассоновская случайная величина.
- •Функции распределения случайных величин. Ее свойства и график.
- •Математическое ожидание и его свойства. Вычисление математического ожидания по выбору
- •Дисперсия случайной величины и ее свойства.
- •Вычисление дисперсии по выбору
- •Числовые характеристики непрерывных случайных величин. Функции распределения и функции плотности случайных величин. Их графики.
- •Функция распределения и функция плотности распределения. Графики функций
- •Гауссовское распределение. Условия нормировки.
- •Определение математического ожидания непрерывной случайной величины. Вычисление мат ожидания по выбору
- •Дисперсия непрерывной случайной величины. Вычисление дисперсии по выбору.
- •Вероятность попадания случайной величины в заданный промежуток. Правило трех сигм
- •Момент случайных величин. Асимметрия и эксцесс
- •Определение двумерной случайной величины, ее распределение и свойства.
- •Корреляционный момент. Ковариация случайной величины и ее свойства. Коэффициент ковариации и его свойства
- •Двумерное равномерное распределение
- •Неравенство Чебышева. Неравенство Маркова
- •Теорема Чебышева. Теорема Маркова. Теорема Бернулли.
- •Двумерная случайная величина неопределенного типа. Свойства функций плотности.
- •Центральная предельная теорема. Теорема Ляпунова и Леви.
- •Предмет математической статистики. Генеральная совокупность. Выборка. Объем выборки. Репрезентативная (представительная) выборка. Полигон частот
- •Эмпирический закон распределения. Эмпирическая функция распределения. Гистограмма.
- •Точечные оценки параметров распределения и их свойства. Выборочное среднее и выборочная дисперсия.
- •Смещенность выборочной дисперсии. Исправленная дисперсия.
- •Метод моментов
- •Метод наибольшего правдоподобия
- •Метод наименьших квадратов
- •Интервальное оценивание параметров распределения. Доверительный интервал
- •Интервальная оценка мат ожидания при неизвестной дисперсии
- •Оценка мат ожидания при известной дисперсии.
- •Основные понятия проверки гипотез.
- •Ошибка первого и второго рода. Мощность критерия.
- •Гипотеза о равенстве средних при известной дисперсии
- •37. Гипотеза о равенстве средних при неизвестной дисперсии
- •38. Гипотеза о равенстве дисперсии при неизвестных средних
-
Предмет теории вероятности. Случайные события. Пространство элементарных событий. Операции над событиями.
Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные.
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность событий S.
Невозможными называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность событий S.
Случайным называют событие, которое при осуществлении совокупности событий S либо произойдет, либо не произойдет.
Предметом теории вероятности является изучение вероятностных закономерностей массовых однородных случайных событий.
Построение логически полноценной теории вероятностей основана на аксиоматическом определении случайного события и его вероятности. В системе аксиом, предложенной Колмогоровым, неопределяемыми понятиями являются элементарные события и вероятность. Аксиомы, определяющие вероятность:
-
Каждому событию А поставлено в соответствие неотрицательное действительное число P(A). Это число называется вероятностью события А.
-
Вероятность достоверного события равна единице:
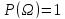
-
Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.
Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем.
Виды случайных событий:
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Несколько событий образуют полную группу, если в результате испытания появляется хотя бы одно из них.
Если события, образующие полную группу, попарно несовместны, то в результате испытания появляется одно и только одно из этих событий.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным чем другое.
Множество всех элементарных событий, которые могут появиться в испытании, называют пространством элементарных событий, а сами элементарные события – точками пространства.
Операции над событиями:
1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. При этом если элементарное событие входит и в A, и в B, то в C оно входит один раз. В результате испытания событие C происходит тогда, когда произошло событие, которое входит или в A или в B. Сумма произвольного количества событий состоит из всех элементарных событий, которые входят в одно из Ai, i=1, ..., m.
B A 
2. Событие C произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B. Произведением произвольного числа событий называется событие состоящее из элементарных событий, входящих во все Ai, i=1, ..., m.

3. Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.

4.
Событие называется противоположным
событию A, если оно удовлетворяет двум
свойствам. Формулы де Моргана:
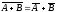 и
и
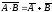

5. События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания. События A и B называются несовместными, если они не имеют общих элементарных событий. C=AB=V Тут V - пустое множество.
