5. Определение дискретной случайной величины. Закон распределения случайной величины. Биноминальная и Пуассоновская случайная величина.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

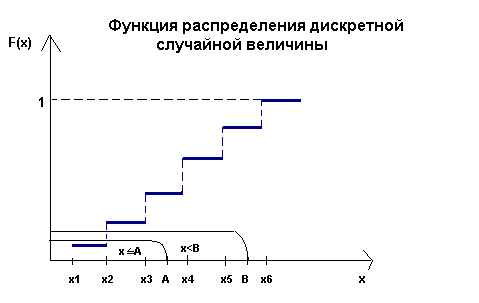
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

Х х₁ х₂… х_n

P p₁ p₂ … p_n

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события Х=х_1; Х=х_2, …, Х= х_n образуют полную группу; следовательно, сумма вероятностей второй строки таблицы, равна единице: 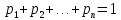. Если множество возможных значений Х бесконечно, то ряд 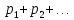сходится и его сумма равна единице.

Биноминальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биноминальным» потому, что правую часть равенства 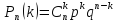можно рассматривать как общий член разложения бинома Ньютона:

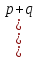
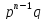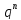Таким образом, первый член разложения pⁿ определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член определяет вероятность события n-1 раз; …; последний член определяет вероятность того, что событие не появится ни разу.

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:

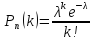 – среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p≤0,1 и np≤10. События, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).

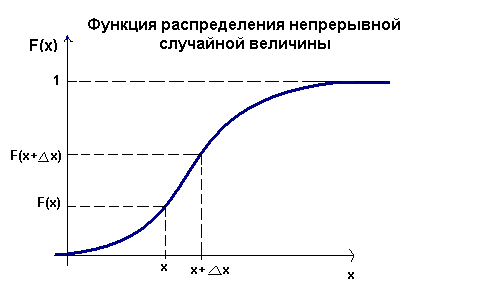
6. Функции распределения случайных величин. Ее свойства и график.

Функцией распределения вероятностей F(x) случайной величины Х в точке х называется вероятность того, что в результате опыта случайная величина примет значение, меньше, чем х, т.е. F(x)=P{X < х}. 

Рассмотрим свойства функции F(x):

1. F(-∞)=lim_(x→-∞)F(x)=0. Действительно, по определению, F(-∞)=P{X < -∞}. Событие (X < -∞) является невозможным событием: F(-∞)=P{X < - ∞}=p{V}=0.

2. F(∞)=lim_(x→∞)F(x)=1, так как по определению, F(∞)=P{X < ∞}. Событие Х < ∞ является достоверным событием. Следовательно, F(∞)=P{X < ∞}=p{U}=1.

3. Вероятность того, что случайная величина примет значение из интервала [Α Β] равна приращению функции распределения вероятностей на этом интервале. P{Α ≤X<Β}=F(Β)-F(Α).

4. F(x₂)≥ F(x₁ ), если x_2, > x₁, т.е. функция распределения вероятностей является неубывающей функцией.