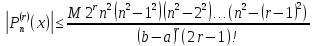- •Предмет теории вероятности. Случайные события. Пространство элементарных событий. Операции над событиями.
- •Классическое определение вероятности. Теорема сложения несовместных событий. Геометрические вероятности.
- •3.Условная вероятность. Формула полной вероятности. Формула Бейеса.
- •Повторные независимые испытания. Формула Бернулли. Локальная и интегральная теорема Лапласа.
- •Определение дискретной случайной величины. Закон распределения случайной величины. Биноминальная и Пуассоновская случайная величина.
- •Функции распределения случайных величин. Ее свойства и график.
- •Математическое ожидание и его свойства. Вычисление математического ожидания по выбору
- •Дисперсия случайной величины и ее свойства.
- •Вычисление дисперсии по выбору
- •Числовые характеристики непрерывных случайных величин. Функции распределения и функции плотности случайных величин. Их графики.
- •Функция распределения и функция плотности распределения. Графики функций
- •Гауссовское распределение. Условия нормировки.
- •Определение математического ожидания непрерывной случайной величины. Вычисление мат ожидания по выбору
- •Дисперсия непрерывной случайной величины. Вычисление дисперсии по выбору.
- •Вероятность попадания случайной величины в заданный промежуток. Правило трех сигм
- •Момент случайных величин. Асимметрия и эксцесс
- •Определение двумерной случайной величины, ее распределение и свойства.
- •Корреляционный момент. Ковариация случайной величины и ее свойства. Коэффициент ковариации и его свойства
- •Двумерное равномерное распределение
- •Неравенство Чебышева. Неравенство Маркова
- •Теорема Чебышева. Теорема Маркова. Теорема Бернулли.
- •Двумерная случайная величина неопределенного типа. Свойства функций плотности.
- •Центральная предельная теорема. Теорема Ляпунова и Леви.
- •Предмет математической статистики. Генеральная совокупность. Выборка. Объем выборки. Репрезентативная (представительная) выборка. Полигон частот
- •Эмпирический закон распределения. Эмпирическая функция распределения. Гистограмма.
- •Точечные оценки параметров распределения и их свойства. Выборочное среднее и выборочная дисперсия.
- •Смещенность выборочной дисперсии. Исправленная дисперсия.
- •Метод моментов
- •Метод наибольшего правдоподобия
- •Метод наименьших квадратов
- •Интервальное оценивание параметров распределения. Доверительный интервал
- •Интервальная оценка мат ожидания при неизвестной дисперсии
- •Оценка мат ожидания при известной дисперсии.
- •Основные понятия проверки гипотез.
- •Ошибка первого и второго рода. Мощность критерия.
- •Гипотеза о равенстве средних при известной дисперсии
- •37. Гипотеза о равенстве средних при неизвестной дисперсии
- •38. Гипотеза о равенстве дисперсии при неизвестных средних
-
Определение двумерной случайной величины, ее распределение и свойства.
Совокупность двух случайных величин, заданных на вероятностном пространстве, называют двумерными случайными величинами или двумерным вектором; x и y называют векторами случайных величин.
Функции распределения случайных векторов (x;y) называют вероятностью их совместного наступления.
Свойства:
-
0≤F(x;y)≤1
-
F(x;y) является нечетной функцией по каждому из своих аргументов при фиксированном другом аргументе. Если х1<х2, F(x;y)≤ F(x1;х2).
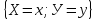
-
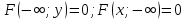
-
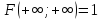
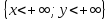 -
достоверные
события
-
достоверные
события
-
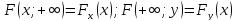
-
Функция F(x;y) является непрерывной слева по каждому из аргументов
-
В случае одной случайной величины:
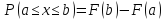 .
Две случайные величины:
.
Две случайные величины:
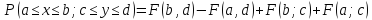
-
Корреляционный момент. Ковариация случайной величины и ее свойства. Коэффициент ковариации и его свойства
Корреляционный момент – это момент от математического ожидания. Обозначается COV (X;Y)=M(x-M(X))(y-M(Y))
Свойства:
-
COV(x;y)=Mxy-MxMy
-
COV (x;x)=D(X)
-
Если x и y независимы, то их ковариация равна нулю: COV(x;y)=0
Если у случайной величины ковариация равна нулю, то они называются не корреляционными
-
COV (ax+b; cy+b)=ac COV(x;y)
-
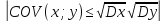
-
Для того, чтобы случайные величины были линейно зависимы Y=ax+b необходимо достаточно, чтобы выполнялось равенство в 5 пункте
Коэффициентом корреляции называют отношение ковариации к квадратному корню дисперсии.
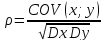
Свойства:
-
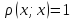
-
Если x и y независимы, то коэффициент корреляции равен нулю.
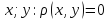
-
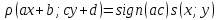
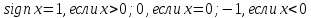
-
-1≤
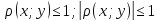
-
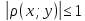 тогда
и только тогда, когда x
и y
линейно зависимы
тогда
и только тогда, когда x
и y
линейно зависимы
-
Двумерное равномерное распределение
Система
двух случайных величин называется
равномерно распределенной на плоскости,
если ее плотность вероятности f(x,
y)
= const
внутри некоторой области и равна 0 вне
ее. Пусть данная область – прямоугольник
вида
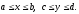 Тогда
из свойств f(x,
y)
следует, что
Тогда
из свойств f(x,
y)
следует, что
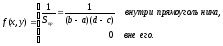
Найдем двумерную функцию распределения:
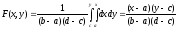 при
a
< x
< b,
c
< y
< d,
F(x,
y)
= 0 при x
≤ a
или
y
≤ c,
F(x,
y)
= 1 при x
≥ b,
y
≥ d.
при
a
< x
< b,
c
< y
< d,
F(x,
y)
= 0 при x
≤ a
или
y
≤ c,
F(x,
y)
= 1 при x
≥ b,
y
≥ d.
Функции
распределения составляющих, вычисленные
по формулам, приведенным в свойстве 4
функции распределения, имеют вид:
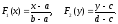
-
Неравенство Чебышева. Неравенство Маркова
Неравенство Чебышева, используемое для доказательства дальнейших теорем, справедливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.
(неравенство Чебышева). p( | X – M(X)| < ε ) ≥ D(X) / ε². (13.1)
Доказательство. Пусть Х задается рядом распределения
|
Х |
х1 |
х2 |
… |
хп |
|
р |
р1 |
р2 |
… |
рп |
Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то
р ( |X – M(X)| < ε ) + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).
D(X) = (x1 – M(X))²p1 + (x2 – M(X))²p2 + … + (xn – M(X))²pn . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда D(X) ≥ (xk+1 – M(X))²pk+1 + (xk+2 – M(X))²pk+2 + … + (xn – M(X))²pn ≥ ε² (pk+1 + pk+2 + … + pn).
Отметим, что pk+1 + pk+2 + … + pn есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требовалось доказать.
МАРКОВА
НЕРАВЕНСТВО: для производной от
алгебраического многочлена - неравенство,
дающее оценку максимального значения
этой производной через наибольшее
значение самого многочлена. Пусть Р п (х).-
алгебраич. многочлен степени не выше
пи 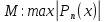
a≤x≤b
Тогда
для любого х
из отрезка [ а,
b]выполняется
неравенство
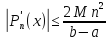
Неравенство
получено А. А. Марковым в 1889. М. н. является
точным. Так, если a= -1, b=1,
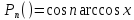 ,
то
,
то 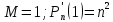
и в неравенстве достигается знак равенства.
Для
производной любого порядка 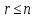 из
М. н. следует соотношение
из
М. н. следует соотношение
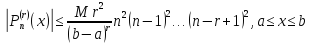
к-рое
при 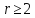 уже
не является точным. Точное неравенство
для
уже
не является точным. Точное неравенство
для 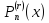 получено
В. А.
Марковым [2]:
получено
В. А.
Марковым [2]: