2. Классическое определение вероятности. Теорема сложения несовместных событий. Геометрические вероятности.

Вероятность есть число, характеризующее степень возможности появления события. Каждый из возможных результатов испытания называется элементарным исходом (элементарным событием). Элементарные исходы, в которых интересующие нас события наступают, называются благоприятствующими.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов в общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность события А определяется формулой 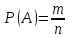, где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.

Из определения вероятности вытекают следующие свойства:

1. Вероятность достоверного события равна единице: если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно,

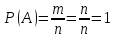
2. Вероятность невозможного события равна нулю: если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m=0, следовательно,

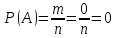
3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей: случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0<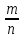<1, следовательно, 0<P(A)<1.

Вероятность любого события удовлетворяет двойному неравенству 0≤ P(A)≤1.

Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

ТЕОРЕМА: Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

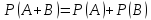
ДОКАЗАТЕЛЬСТВО: введем обозначения: n- общее число возможных элементарных исходов испытания; m₁ – число событий, благоприятствующих событию А; m₂ – число событий, благоприятствующих событию В. Число элементарных исходов, благоприятствующих наступления либо событию А, либо события В, равно m₁+m₂, следовательно,

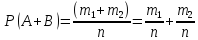
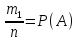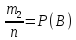Приняв во внимание, что и , окончательно получим

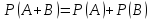
СЛЕДСТВИЕ: вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

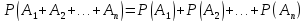
ДОКАЗАТЕЛЬСТВО: рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, А, В и С, равносильно наступлению одного из двух событий, А+В и С, поэтому в силу указанной теоремы

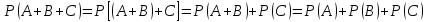
Для произвольного числа попарно несовместных событий доказательство проводится методом математической индукции.

Геометрические вероятности – это вероятности попадания точки в область (отрезок, часть плоскости и т.д.)

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l ∕ Длина L

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством

Р = Площадь g ∕ Площадь G