
- •Утверждаю
- •План Основы построения и эксплуатации рэт ртв пво
- •Тема 1 основные принципы и методы радиолокации
- •Учебные вопросы и распределение времени (слайд №3).
- •Задачи курса обучения
- •Основные определения радиолокации
- •Первый принцип радиолокации
- •Диффузное или рассеянное отражение
- •Дифракция
- •Второй принцип радиолокации
- •Третий принцип радиолокации
- •Так как за время tз волна проходит расстояние, равное удвоенной дальности, то
- •Четвертый учебный вопрос Виды радиолокации
- •Заключительная часть
- •Руководитель занятия:
- •Учебные вопросы и распределение времени (слайд №3).
- •1. Местоположение летательного аппарата относительно рлс определяется тремя пространственными координатами
- •3. Виды радиолокации
- •Параметры рлс
- •Параметры цели
- •Из последней формулы определим дальность действия рлс
- •А. Влияние параметров передатчика (Ри) Из уравнения (1) следует, что
- •Б. Влияние параметров антенны (g и Sa)
- •Эффективная отражающая поверхность цели учитывает:
- •Поскольку сложного объекта (ракеты, самолета и т.П.) рассчитать достаточно трудно, то практически её определяют экспериментальным путем. При расчетах можно использовать следующие данные в м2.
- •Поскольку Rз во много раз больше ha и Нц, то
- •Рефракция и сверхрефракция
- •Подполковник запаса ж.Атчабаров
- •Учебные вопросы и распределение времени (слайд №3).
- •Наибольшее распространение и радиолокационной технике получил импульсный метод. Импульсный метод радиолокации
- •Принцип работы импульсной рлс
- •Заключительная часть
- •Утверждаю
- •Учебные вопросы и распределение времени (слайд №3).
- •Отношение длительности импульса на входе сжимающего фильтра τu к длительности импульса на выходе τu2 называется коэффициентом сжатия к
- •Второй учебный вопрос.
- •На изменение фазы отраженного сигнала влияет радиальная составляющая νr скорости цели.
- •Отраженный сигнал от цели запишется
- •Метод пеленгации по максимуму
- •Метод пеленгации по минимуму
- •Метод равносигнальной зоны
- •Заключительная часть
- •Подполковник запаса ж.Атчабаров
- •Круговой обзор
- •Секторный обзор
- •Винтовой обзор
- •Спиральный обзор
- •Конический обзор
- •Пилообразный обзор
- •Строчный обзор
- •Принцип измерения высоты целей в современных рлс
- •Заключительная часть
- •Утверждаю
- •Поскольку Rз во много раз больше ha и Нц, то
- •Подполковник запаса ж.Атчабаров
Строчный обзор
Строчный обзор – разновидность пилообразного обзора.
ВЫВОД
Рассмотренные выше методы обзора пространства в РЛС, использующих однолучевые антенны, позволяют одновременно определять одну (круговой и секторный обзоры) или обе угловые координаты всех целей, находящихся в заданной части пространства.
Периоды обзора пространства слишком велики и не всегда обеспечивают необходимой информацией о местоположении современных скоростных воздушных целей.
Необходимость уменьшения периода обзора пространства привела к созданию многолучевых РЛС. Антенные системы таких РЛС создают два и более лучей, что позволяет уменьшить период обзора и повысить точность определения угловых координат за счет сравнения сигналов, принятых различными лучами.
Второй учебный вопрос.
Принцип определения высоты полета целей
В предыдущем учебном вопросе были рассмотрены методы определения угловых координат целе βо и εо . Однако, на практике для обеспечения боевых действий истребительной авиации целесообразно выдавать третью координату, определяющую пространственное положение цели не как угол места цели εо , а выдавать данные о высоте полета цели над поверхностью земли Нц, так как на большей части маршрута самолеты летят, как правило, на одной высоте, а угол места непрерывно изменяется.
В радиолокации
высота полета цели Нц
измеряется путем определения угла места
εо
и наклонной дальности Дн
. При известных значениях угла места и
наклонной дальности высоты цели Н1
для ровной горизонтальной поверхности
определяется тригонометрическим путем
(рис. 5.6, слайд 57)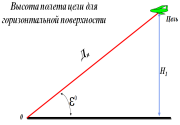
Н1 = Дн ∙sinεо.
Однако в этом уравнении не учитываются такие факторы, как атмосферная рефракция и кривизна земной поверхности. Атмосферная рефракция может быть учтена путем замены действительного радиуса Земли Rз так называемым эффективным радиусом Земли. Для нормальной атмосферной рефракции Rэ
Rэ = 4/3 Rэ= 4/3 ·6370 = 8500; Rэ = 8500 км.
Для реальных условий Рис. 5.7 (слайд 41, 58), когда Нц <<Rз и Дн <<Rз
Нц = Н1 + Н2,
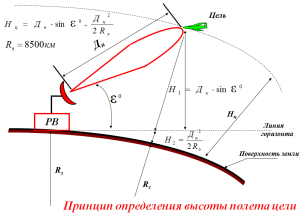
где Н1 = Дн ·sinεо - высота цели относительно линии горизонта;
Н2 = Д2 н/2Rэ - поправка на кривизну Земли, зависящая от дальности цели.
Тогда
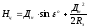 .
(5.5)
.
(5.5)
Из уравнения (5.5) видно, что задача определения высоты полета цели сводится к измерению угла места цели и дальности.
Наиболее
распространенным методом измерения
угла места цели в сантиметровом диапазоне
волн является метод
максимума
с качанием луча в вертикальной плоскости.
Для реализации этого метода ДНА должна
быть широкой в горизонтальной плоскости
и узкой в вертикальной. Такая ДНА качается
в вертикальной плоскости, дважды облучая
цель за период
качания (рис. 5.8. слайд 42, 59).
Управление ДНА осуществляется механически поворотом всей антенной системы.
Отраженные сигналы наблюдаются на экране ЭЛТ с яркостной индикацией цели в прямоугольной системе координат ДАЛЬНОСТЬ-ВЫСОТА. Развертка высоты (вертикальная развертка) создается подачей на вертикально отклоняющие катушки ЭЛТ напряжения, пропорционального углу наклона антенны (ДНА), которое вырабатывается в специальном счетно-решающем устройстве.
Достоинствами данного метода определения высоты цели являются простота и высокая точность.
Метод максимума также используется при определении угла места с использованием парциальных диаграмм (парциальный – частичный, составляющая часть чего-то). Сущность этого метода состоит в том, что создается веерообразная ДНА в вертикальной плоскости. При этом каждый лепесток облучает пространство в определенном секторе по углу места и на своей рабочей длине волны (рис. 5.9, слайд 43, 60).

Приемное устройство имеет число каналов, равное числу лепестком. Для определения угла места цели достаточно узнать канал, по которому ведется прием отраженных сигналов.
Достоинства этого метода:
способность определять высоту полета цели на «проходе»;
простота отсчета высоты.
Недостатки:
сложность антенного и приемо-передающего устройства;
точность определения высоты зависит от ширины лепестков парциальной диаграммы в вертикальной плоскости.
Третий учебный вопрос.
