Добавил:

pmaxim2006 fizmathim.ru Решаю задачи по высшей математике. Фотографии решенных заданий по высшей математике https://fizmathim.ru/photo/ Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Павлодарский государственный университет им. С. Торайгырова

Предмет:

Математика

Файл:

ИДЗ 14.2 Рябушко пример решения

.pdf

Скачиваний:

Добавлен:

20.02.2017

Размер:

189.82 Кб

Скачать

☆

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

ИДЗ 14.2 – Вариант 0

1. Показать, что данное выражение является полным дифференциалом функции u(x, y). Найти функцию u(x, y)

1.0. (4x3y3 – y2)dx + (3x4y2 – 2xy)dy

Проверим, выполняется ли условие полного дифференциала

для функции u(x, y). Имеем:

P x, y 4x3 y3

y2 ; Q x, y 3x 4 y2 2xy

тогда

4x3 y3

y2 4x3 y3 y y2 y 4x3

3y3 1

2y2 1

12x3 y2

4 1

2xy

2xy x

3 4x

12x

Так как выполняется условие

, то данное выражение является полным дифференциалом

функции u(x, y).

Положив x0 = 1, y0 = 1, по формуле (1) найдем u(x, y)

u x, y P x, y0 dx Q x, y dy C

Вычисляем:

4 2

u x, y 4x

dx 3x

2xy dy 4x

1 dx 3x y

2xy dy

2xy

x 4 x

x 4 y3

xy 2

4 x 14

1 x

4 y3 xy 2 x 4

x 12

x 4 x x 4 y3 xy 2 x 4 x x 4 y3 xy 2 C

Результат верен, если

u x, y

P x, y ,

u x, y Q x, y

Сделаем проверку:

4 y3 xy 2

x 4 y3 x

xy 2

4 1y3 y

2 4x3 y3 y2

4 y3

xy 2

x 4 y3 y

xy 2

4 y3 1 x

2y2 1 3x 4 y2 2xy

Ответ: u x, y x 4 y3

xy 2 C

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

2. Решить следующие задачи

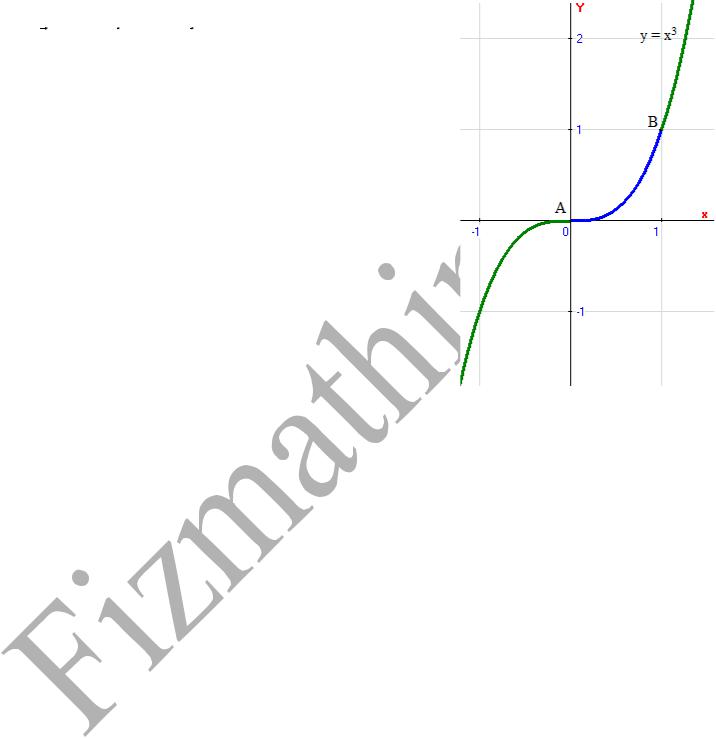
2.0. Вычислить работу силы F = (x2 + y2 + 1)i + 2xyj вдоль дуги параболы y = x3, заключенной между точками A(0, 0) и B(1, 1).

Решение:

Пусть F P x, y i Q x, y j есть переменная сила,

совершающая работу А вдоль пути L, функции P(x, y) и Q(x, y) непрерывны на кривой L, тогда работа силы равна

A P x, y dx Q x, y dy

y = x3 dy = 3x2dx

Переменная x в данном направлении изменяется от x1 = 0 до x2 = 1

Пределы интегрирования 0 ≤ x ≤ 1

Тогда работа силы А равна:

A x				2	y			2							1		2	x		3	2					x		3	3x		2	dx		1		2	x		6	1 dx				6x	6	dx
A x					y				1 dx 2xydy x									x				1 dx 2x				x			3x			dx	x				x			1 dx				6x		dx
	L														0																			0
1												1												3		7				1				3							1		3
																								3		7				1				3							1		3
																						x			7x							x										1
		2				6					6			2				6				x			7x							x					7					1			7
x			x				1 6x					dx x				7x			1 dx								x								x			x						1			1
x			x				1 6x					dx x				7x			1 dx				3		7		x						3		x			x					3	1			1
0												0											3		7					0			3								0		3
0												0																		0											0
	03									1			1				7
		07				0					1 1			2
		07				0					1 1			2
	3									3			3				3
	3									3			3				3

Соседние файлы в предмете Математика

#
20.02.2017291.86 Кб207ИДЗ 12.2 Рябушко пример решения.pdf
#
20.02.2017279.38 Кб292ИДЗ 13.1 Рябушко пример решения.pdf
#
20.02.2017274.9 Кб126ИДЗ 13.2 Рябушко пример решения.pdf
#
20.02.2017252.34 Кб69ИДЗ 13.3 Рябушко пример решения.pdf
#
20.02.2017248.61 Кб99ИДЗ 14.1 Рябушко пример решения.pdf
#
20.02.2017189.82 Кб47ИДЗ 14.2 Рябушко пример решения.pdf
#
20.02.2017305.45 Кб99ИДЗ 15.1 Рябушко пример решения.pdf
#
20.02.2017240.54 Кб87ИДЗ 15.2 Рябушко пример решения.pdf
#
20.02.2017255.44 Кб499ИДЗ 2.1 Рябушко пример решения.pdf
#
20.02.2017248.21 Кб305ИДЗ 2.2 Рябушко пример решения.pdf
#
20.02.2017218.55 Кб342ИДЗ 3.1 Рябушко пример решения.pdf