- •1. Предмет курса «Гидравлика и гидропривод». Основные этапы развития гидравлики как инженерной науки.
- •2. Физическое понятие жидкости как агрегатного состояния вещества.
- •3. Реальная и идеальная жидкость. Понятие вязкости.
- •4.1 Вязкость, как свойство жидкости.
- •4.2 Вязкость, как свойство жидкости.
- •5. Основные физические свойства реальных жидкостей.
- •6. Поверхностное натяжение. Капиллярный эффект.
- •7. Классификация сил, действующих на жидкость.
- •8.1 Свойства гидростатического давления.
- •8.2 Свойства гидростатического давления.
- •9. Уравнение равновесия покоящейся жидкости.
- •10. Основное уравнение гидростатики.
- •11. Понятие абсолютного и избыточного давления. Пьезометрическая высота. Вакуум.
- •12.1 Приборы для измерения давления.
- •12.2 Приборы для измерения давления.
- •13. Сообщающиеся сосуды. Закон Паскаля.
- •14.1 Относительный покой жидкости.
- •14.2 Относительный покой жидкости.
- •15. Поверхности равного давления.
- •16. Сила гидростатического давления, действующая на плоскую фигуру.
- •17. Определение положения центра давления на плоскую фигуру. Понятие эксцентриситета давления.
- •18. Сила гидростатического давления.
- •19. Построение эпюр гидростатического давления.
- •20. Закон Архимеда, плавание тел.
- •21. Линия тока, элементарная струйка.
- •22. Классификация видов движения жидкости.
- •23. Понятие расхода жидкости, средней скорости, живого сечения, гидравлического радиуса, смоченного периметра.
- •24. Дифференциальное уравнение неразрывности потока.
- •25. Дифференциальное уравнение движения идеальной жидкости.
- •26. Вывод уравнения Бернулли для идеальной жидкости.
- •27. Геометрическая и энергетическая интерпретация уравнения Бернулли.
- •28. Уравнение Бернулли для элементарной струйки реальной жидкости.
- •29. Уравнение Бернулли для потока реальной жидкости.
- •30.1 Пример использования уравнения Бернулли в технике.
- •30.2 Пример использования уравнения Бернулли в технике.
- •31. Понятие ламинарного и турбулентного режимов движения реальных жидкостей.
- •32. Критическое значение критерия Рейнольдса и его вывод.
- •33. Ламинарный режим движения. Распределение скорости жидкости по сечению потока.
- •34. Определение расхода жидкости и средней скорости ламинарного потока.
- •35. Понятие пульсационной, мгновенной, осредненной и средней скоростей течения.
- •36.1 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •36.2 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •37.1 Дифференциальное уравнение движения реальной жидкости Навье-Стокса.
- •39. Природа потерь напора, их связь с режимом движения жидкости.
- •40. Уравнение Дарси-Вейсбаха для расчета потерь напора по длине трубопровода.
- •41.1 Понятие гидравлически гладких и шероховатых труб.
- •41.2 Понятие гидравлически гладких и шероховатых труб.
- •42.1 Потери напора при турбулентном режиме движения.
- •42.2 Потери напора при турбулентном режиме движения.
- •43. Графики Никурадзе.
- •44.1 Условие возникновения местных потерь напора.
- •44.2 Условие возникновения местных потерь напора.
- •45. Резкое расширение трубопровода. Формула Борда.
- •46. Случаи местных сопротивлений, наиболее часто встречающиеся в инженерной практике.
- •47.1 Истечение жидкости через отверстие. Типы сжатия струи.
- •47.2 Истечение жидкости через отверстие. Типы сжатия струи.
- •48. Коэффициенты истечения и
- •49. Определение коэффициентов ипри истечении жидкости через малое и большое отверстие в тонкой стенке.
- •50. Определение коэффициентов ипри истечении жидкости через затопленное малое отверстие.
- •51. Истечение через насадки. Типы и применение насадков.
- •52.1 Истечение жидкости через внешний цилиндрический насадок.
- •52.2 Истечение жидкости через внешний цилиндрический насадок.
- •53. Истечение жидкости через отверстие при переменном напоре. Время опорожнения сосуда.
- •54. Классификация трубопроводов.
- •55.1 Гидравлический расчет простых трубопроводов.
- •55.2 Гидравлический расчет простых трубопроводов.
- •56 Характеристика трубопроводов. Кривые потребного напора.
- •57.1 Последовательное и параллельное соединение простых трубопроводов.
- •57.2 Последовательное и параллельное соединение простых трубопроводов.
- •58. Расчет разветвленного трубопровода.
- •59. Классификация насосов.
- •60. Принцип действия динамических насосов.
- •61. Основные характеристики насосов.
- •62.1 Устройство и принцип действия центробежного насоса.
- •62.2 Устройство и принцип действия центробежного насоса.
- •63. Движение жидкости в рабочем колесе центробежного насоса.
- •64. Основное уравнение центробежного насоса.
- •65.1 Характеристики центробежного насоса.
- •65.2 Характеристики центробежного насоса.
- •66. Законы пропорциональности для центробежных насосов.
- •67.1 Совместная работа насоса и трубопровода.
- •67.2 Совместная работа насоса и трубопровода.
- •68. Определение рабочей точки системы насос-трубопровод.
- •69.1 Регулирование подачи центробежных насосов.
- •69.2 Регулирование подачи центробежных насосов.
- •70.1 Последовательное и параллельное соединение насосов.
- •70.2 Последовательное и параллельное соединение насосов.
- •71. Общие сведения об объемных насосах.
- •72. Принцип действия объемных насосов.
- •73.1 Рабочие характеристики объемных насосов.
- •73.2 Рабочие характеристики объемных насосов.
- •74. Устройство и принцип действия поршневых насосов.
- •75. Роторные насосы.
- •76.1 Объемный гидропривод. Основные понятия и определения.
- •76.2 Объемный гидропривод. Основные понятия и определения.
- •77.1 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
- •77.2 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
12.2 Приборы для измерения давления.
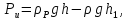
 где
где
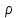 – плотность жидкости, заполняющей сосуд
и левое колено прибора (до уровня рабочей
жидкости);
– плотность жидкости, заполняющей сосуд
и левое колено прибора (до уровня рабочей
жидкости); – плотность рабочей жидкости;
– плотность рабочей жидкости; – разность уровней точки
– разность уровней точки и рабочей жидкости в левом колене.Дифференциальный
манометр
применяется для измерения разности
давлений. Разность
давлений может быть определена путем
измерения каждого из давлений в
отдельности. Однако таким способом
нельзя воспользоваться в тех случаях,
когда разность давлений мала, а каждое
из давлений велико, ибо для получения
достаточно высокой точности измерения
малой разности измерение каждого из
больших давлений должно быть выполнено
со значительно более высокой, практически
недостижимой, точностью. Поэтому
для измерения разности давлений
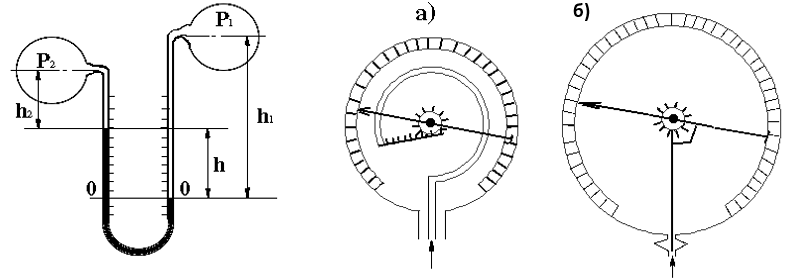
применяются специальные приборы. На
рис. изображена схема U-образного
дифференциального манометра. Он состоит
из U-образной стеклянной трубки, примерно
до середины заполненной рабочей
жидкостью. Под действием разности
давлений рабочая жидкость в коленах
перемещается. Для горизонтальной
плоскости равного давления 0-0 можно
записать:
и рабочей жидкости в левом колене.Дифференциальный
манометр
применяется для измерения разности
давлений. Разность
давлений может быть определена путем
измерения каждого из давлений в
отдельности. Однако таким способом
нельзя воспользоваться в тех случаях,
когда разность давлений мала, а каждое
из давлений велико, ибо для получения
достаточно высокой точности измерения
малой разности измерение каждого из
больших давлений должно быть выполнено
со значительно более высокой, практически
недостижимой, точностью. Поэтому
для измерения разности давлений
применяются специальные приборы. На
рис. изображена схема U-образного
дифференциального манометра. Он состоит
из U-образной стеклянной трубки, примерно
до середины заполненной рабочей
жидкостью. Под действием разности
давлений рабочая жидкость в коленах
перемещается. Для горизонтальной
плоскости равного давления 0-0 можно
записать:
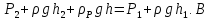 идно,
что разность давлений по показанию
манометра определяется следующим
образом:
идно,
что разность давлений по показанию
манометра определяется следующим
образом:
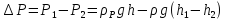 .
Если точки, где измеряется давление,
находятся на одном уровне, то
.
Если точки, где измеряется давление,
находятся на одном уровне, то
 В этом случае
В этом случае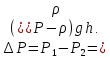 Из
других жидкостных приборов находят
широкое применение микроманометры
(пьезометры с наклонной трубкой), чашечные
манометры и вакуумметры, а также
дифференциальные пьезометры.
Из
других жидкостных приборов находят
широкое применение микроманометры
(пьезометры с наклонной трубкой), чашечные
манометры и вакуумметры, а также
дифференциальные пьезометры.
Механические приборы используются в тех случаях, когда более точные, жидкостные, не могут применяться из-за чрезмерно больших измеряемых давлений. В некоторых конструкциях механических манометров и вакуумметров используются упругие рабочие элементы (например, полые пружины, гибкие диафрагмы, сильфоны и т.п.), которые деформируются под действием давления жидкости. На схемах приведены две принципиальные схемы таких приборов.
13. Сообщающиеся сосуды. Закон Паскаля.
Сообщающимися сосудами называют сосуды, соединенные друг с другом таким образом, чтобы жидкость свободно перетекала из одного сосуда в другой. Закон сообщающихся сосудов гласит: в открытых сообщающихся сосудах при равновесии жидкости давление на любом горизонтальном уровне одинаково. Если в открытые сообщающиеся сосуды налита одинаковая жидкость, то независимо от формы сосудов жидкость в обоих сосудах жидкость будет находится на одном уровне (рис.).
Если
заполнить открытые сообщающиеся сосуды
двумя несмешивающимися жидкостями,
имеющими плотности
 и
и ,
например, ртутью и водой, то жидкость
также распределится таким образом,
чтобы давления этих жидкостей на любом
горизонтальном уровне в обоих сосудах
было одинаково. Выберем горизонтальный
уровень жидкости AB, ниже которого
жидкость однородна. Тогда
,
например, ртутью и водой, то жидкость
также распределится таким образом,
чтобы давления этих жидкостей на любом
горизонтальном уровне в обоих сосудах
было одинаково. Выберем горизонтальный
уровень жидкости AB, ниже которого
жидкость однородна. Тогда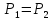 .
.
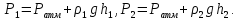
Откуда
следует, что
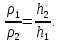 Это уравнение представляет собой условие
равновесия жидкостей в сообщающихся
сосудах. На законе сообщающихся сосудов
основано действие шлюзов, фонтанов и
других устройств. Французский
ученыйБ. Паскальв
середине XVII века эмпирически установил
закон, названный законом Паскаля:
Давление в жидкости или газе передается
во всех направлениях одинаково и не
зависит от ориентации площадки, на
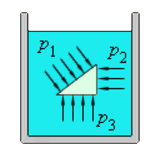
которую оно действует. Для иллюстрации
закона Паскаля на рис. изображена
небольшая прямоугольная призма,
погруженная в жидкость. Если предположить,
что плотность материала призмы равна
плотности жидкости, то призма должна
находиться в жидкости в состоянии
безразличного равновесия. Это означает,
что силы давления, действующие на грани
призмы, должны быть уравновешены. Это
произойдет только в том случае, если
давления, т. е. силы, действующие на
единицу площади поверхности каждой
грани, одинаковы:
Это уравнение представляет собой условие
равновесия жидкостей в сообщающихся
сосудах. На законе сообщающихся сосудов
основано действие шлюзов, фонтанов и
других устройств. Французский
ученыйБ. Паскальв
середине XVII века эмпирически установил
закон, названный законом Паскаля:
Давление в жидкости или газе передается
во всех направлениях одинаково и не
зависит от ориентации площадки, на
которую оно действует. Для иллюстрации
закона Паскаля на рис. изображена
небольшая прямоугольная призма,
погруженная в жидкость. Если предположить,
что плотность материала призмы равна
плотности жидкости, то призма должна
находиться в жидкости в состоянии
безразличного равновесия. Это означает,
что силы давления, действующие на грани
призмы, должны быть уравновешены. Это
произойдет только в том случае, если
давления, т. е. силы, действующие на
единицу площади поверхности каждой
грани, одинаковы: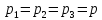 .
.