- •1. Предмет курса «Гидравлика и гидропривод». Основные этапы развития гидравлики как инженерной науки.
- •2. Физическое понятие жидкости как агрегатного состояния вещества.
- •3. Реальная и идеальная жидкость. Понятие вязкости.
- •4.1 Вязкость, как свойство жидкости.
- •4.2 Вязкость, как свойство жидкости.
- •5. Основные физические свойства реальных жидкостей.
- •6. Поверхностное натяжение. Капиллярный эффект.
- •7. Классификация сил, действующих на жидкость.
- •8.1 Свойства гидростатического давления.
- •8.2 Свойства гидростатического давления.
- •9. Уравнение равновесия покоящейся жидкости.
- •10. Основное уравнение гидростатики.
- •11. Понятие абсолютного и избыточного давления. Пьезометрическая высота. Вакуум.
- •12.1 Приборы для измерения давления.
- •12.2 Приборы для измерения давления.
- •13. Сообщающиеся сосуды. Закон Паскаля.
- •14.1 Относительный покой жидкости.
- •14.2 Относительный покой жидкости.
- •15. Поверхности равного давления.
- •16. Сила гидростатического давления, действующая на плоскую фигуру.
- •17. Определение положения центра давления на плоскую фигуру. Понятие эксцентриситета давления.
- •18. Сила гидростатического давления.
- •19. Построение эпюр гидростатического давления.
- •20. Закон Архимеда, плавание тел.
- •21. Линия тока, элементарная струйка.
- •22. Классификация видов движения жидкости.
- •23. Понятие расхода жидкости, средней скорости, живого сечения, гидравлического радиуса, смоченного периметра.
- •24. Дифференциальное уравнение неразрывности потока.
- •25. Дифференциальное уравнение движения идеальной жидкости.
- •26. Вывод уравнения Бернулли для идеальной жидкости.
- •27. Геометрическая и энергетическая интерпретация уравнения Бернулли.
- •28. Уравнение Бернулли для элементарной струйки реальной жидкости.
- •29. Уравнение Бернулли для потока реальной жидкости.
- •30.1 Пример использования уравнения Бернулли в технике.
- •30.2 Пример использования уравнения Бернулли в технике.
- •31. Понятие ламинарного и турбулентного режимов движения реальных жидкостей.
- •32. Критическое значение критерия Рейнольдса и его вывод.
- •33. Ламинарный режим движения. Распределение скорости жидкости по сечению потока.
- •34. Определение расхода жидкости и средней скорости ламинарного потока.
- •35. Понятие пульсационной, мгновенной, осредненной и средней скоростей течения.
- •36.1 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •36.2 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •37.1 Дифференциальное уравнение движения реальной жидкости Навье-Стокса.
- •39. Природа потерь напора, их связь с режимом движения жидкости.
- •40. Уравнение Дарси-Вейсбаха для расчета потерь напора по длине трубопровода.
- •41.1 Понятие гидравлически гладких и шероховатых труб.
- •41.2 Понятие гидравлически гладких и шероховатых труб.
- •42.1 Потери напора при турбулентном режиме движения.
- •42.2 Потери напора при турбулентном режиме движения.
- •43. Графики Никурадзе.
- •44.1 Условие возникновения местных потерь напора.
- •44.2 Условие возникновения местных потерь напора.
- •45. Резкое расширение трубопровода. Формула Борда.
- •46. Случаи местных сопротивлений, наиболее часто встречающиеся в инженерной практике.
- •47.1 Истечение жидкости через отверстие. Типы сжатия струи.
- •47.2 Истечение жидкости через отверстие. Типы сжатия струи.
- •48. Коэффициенты истечения и
- •49. Определение коэффициентов ипри истечении жидкости через малое и большое отверстие в тонкой стенке.
- •50. Определение коэффициентов ипри истечении жидкости через затопленное малое отверстие.
- •51. Истечение через насадки. Типы и применение насадков.
- •52.1 Истечение жидкости через внешний цилиндрический насадок.
- •52.2 Истечение жидкости через внешний цилиндрический насадок.
- •53. Истечение жидкости через отверстие при переменном напоре. Время опорожнения сосуда.
- •54. Классификация трубопроводов.
- •55.1 Гидравлический расчет простых трубопроводов.
- •55.2 Гидравлический расчет простых трубопроводов.
- •56 Характеристика трубопроводов. Кривые потребного напора.
- •57.1 Последовательное и параллельное соединение простых трубопроводов.
- •57.2 Последовательное и параллельное соединение простых трубопроводов.
- •58. Расчет разветвленного трубопровода.
- •59. Классификация насосов.
- •60. Принцип действия динамических насосов.
- •61. Основные характеристики насосов.
- •62.1 Устройство и принцип действия центробежного насоса.
- •62.2 Устройство и принцип действия центробежного насоса.
- •63. Движение жидкости в рабочем колесе центробежного насоса.
- •64. Основное уравнение центробежного насоса.
- •65.1 Характеристики центробежного насоса.
- •65.2 Характеристики центробежного насоса.
- •66. Законы пропорциональности для центробежных насосов.
- •67.1 Совместная работа насоса и трубопровода.
- •67.2 Совместная работа насоса и трубопровода.
- •68. Определение рабочей точки системы насос-трубопровод.
- •69.1 Регулирование подачи центробежных насосов.
- •69.2 Регулирование подачи центробежных насосов.
- •70.1 Последовательное и параллельное соединение насосов.
- •70.2 Последовательное и параллельное соединение насосов.
- •71. Общие сведения об объемных насосах.
- •72. Принцип действия объемных насосов.
- •73.1 Рабочие характеристики объемных насосов.
- •73.2 Рабочие характеристики объемных насосов.
- •74. Устройство и принцип действия поршневых насосов.
- •75. Роторные насосы.
- •76.1 Объемный гидропривод. Основные понятия и определения.
- •76.2 Объемный гидропривод. Основные понятия и определения.
- •77.1 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
- •77.2 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
55.1 Гидравлический расчет простых трубопроводов.
Жидкость
по трубопроводу движется благодаря
тому, что ее энергия в начале трубопровода
больше, чем в конце. Этот перепад уровней
энергии может создаваться несколькими
способами: работой насоса, разностью
уровней жидкости, давлением газа.
Рассмотрим простой трубопровод
постоянного сечения, который расположен
произвольно в пространстве (рис.), имеет
общую длину 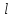 и
диаметр
и
диаметр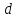 ,
а также содержит ряд местных сопротивлений
(вентиль, фильтр и обратный клапан). В
начальном сечении трубопровода 1-1 геометрическая
высота равна
,
а также содержит ряд местных сопротивлений
(вентиль, фильтр и обратный клапан). В
начальном сечении трубопровода 1-1 геометрическая
высота равна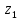 и
избыточное давление
и
избыточное давление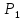 ,
а в конечном сечении 2-2 -
соответственно
,
а в конечном сечении 2-2 -
соответственно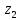 и
и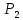 .
Скорость потока в этих сечениях вследствие
постоянства диаметра трубы одинакова
и равна
.
Скорость потока в этих сечениях вследствие
постоянства диаметра трубы одинакова
и равна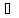 .
Запишем уравнение Бернулли для
сечений 1-1 и 2-2. Поскольку скорость
в обоих сечениях одинакова и
.
Запишем уравнение Бернулли для
сечений 1-1 и 2-2. Поскольку скорость
в обоих сечениях одинакова и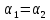 ,
то скоростной напор можно не учитывать.
При этом получим
,
то скоростной напор можно не учитывать.
При этом получим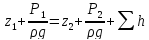 или
или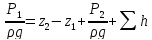 .
Пьезометрическую высоту, стоящую в
левой части уравнения, назовем потребным
напором
.
Пьезометрическую высоту, стоящую в
левой части уравнения, назовем потребным
напором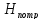 .
Если же эта пьезометрическая высота
задана, то ее называют располагаемым
напором
.
Если же эта пьезометрическая высота
задана, то ее называют располагаемым
напором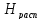 .
Такой напор складывается из геометрической
высоты
.
Такой напор складывается из геометрической
высоты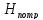 ,
на которую поднимается жидкость,
пьезометрической высоты в конце
трубопровода и суммы всех потерь напора
в трубопроводе. Назовем сумму первых
двух слагаемых статическим напором,
который представим как некоторую
эквивалентную геометрическую высоту
,
на которую поднимается жидкость,
пьезометрической высоты в конце
трубопровода и суммы всех потерь напора
в трубопроводе. Назовем сумму первых
двух слагаемых статическим напором,
который представим как некоторую
эквивалентную геометрическую высоту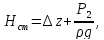 а
последнее слагаемое
а
последнее слагаемое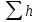 -
как степенную функцию расхода
-
как степенную функцию расхода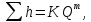 тогда
тогда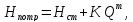 где
где
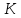 -
величина, называемая сопротивлением
трубопровода;
-
величина, называемая сопротивлением
трубопровода;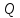 -
расход жидкости;
-
расход жидкости;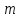 -
показатель степени, который имеет разные
значения в зависимости от режима течения.
Для ламинарного течения при замене
местных сопротивлений эквивалентными
длинами сопротивление трубопровода
равно
-
показатель степени, который имеет разные
значения в зависимости от режима течения.
Для ламинарного течения при замене
местных сопротивлений эквивалентными
длинами сопротивление трубопровода
равно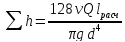 ,
следовательно,
,
следовательно,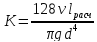 и
и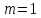 ,
где
,
где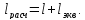 Численные
значения эквивалентных длин
Численные
значения эквивалентных длин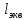 для
различных местных сопротивлений обычно
находят опытным путем. Для турбулентного
течения, используя формулу Вейсбаха-Дарси,
и выражая в ней скорость через расход,
получаем
для
различных местных сопротивлений обычно
находят опытным путем. Для турбулентного
течения, используя формулу Вейсбаха-Дарси,
и выражая в ней скорость через расход,
получаем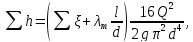 следовательно,
следовательно,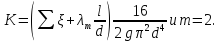 По
этим формулам можно
По
этим формулам можно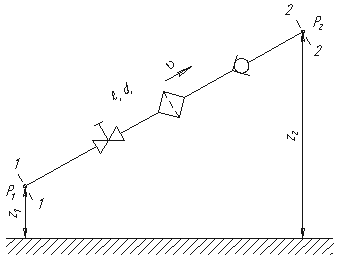
55.2 Гидравлический расчет простых трубопроводов.
построить
кривую потребного напора в зависимости
от расхода. Чем больше расход 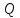 ,
который необходимо обеспечить в
трубопроводе, тем больше требуется
потребный напор
,
который необходимо обеспечить в
трубопроводе, тем больше требуется
потребный напор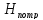 .
При ламинарном течении эта кривая
изображается прямой линией (а), при
турбулентном - параболой с показателем
степени равном двум (б). Крутизна кривых
потребного напора зависит от сопротивления
трубопровода
.
При ламинарном течении эта кривая
изображается прямой линией (а), при
турбулентном - параболой с показателем
степени равном двум (б). Крутизна кривых
потребного напора зависит от сопротивления
трубопровода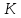 и
возрастает с увеличением длины
трубопровода и уменьшением диаметра,
а также с увеличением местных гидравлических
сопротивлений.
и
возрастает с увеличением длины
трубопровода и уменьшением диаметра,
а также с увеличением местных гидравлических
сопротивлений.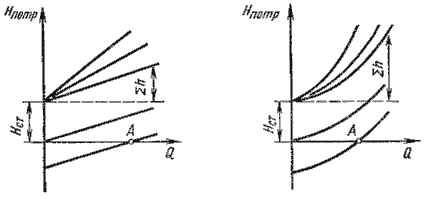
Величина
статического напора 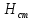 положительна
в том случае, когда жидкость движется
вверх или в полость с повышенным
давлением, и отрицательна при опускании
жидкости или движении в полость с
пониженным давлением. Точка пересечения
кривой потребного напора с осью абсцисс
(точка А) определяет расход при
движении жидкости самотеком. Потребный
напор в этом случае равен нулю. Иногда
вместо кривых потребного напора удобнее
пользоваться характеристиками
трубопровода. Характеристикой
трубопровода называется зависимость
суммарной потери напора (или давления)
в трубопроводе от расхода:
положительна
в том случае, когда жидкость движется
вверх или в полость с повышенным
давлением, и отрицательна при опускании
жидкости или движении в полость с
пониженным давлением. Точка пересечения
кривой потребного напора с осью абсцисс
(точка А) определяет расход при
движении жидкости самотеком. Потребный
напор в этом случае равен нулю. Иногда
вместо кривых потребного напора удобнее
пользоваться характеристиками
трубопровода. Характеристикой
трубопровода называется зависимость
суммарной потери напора (или давления)
в трубопроводе от расхода: