
- •1. Предмет курса «Гидравлика и гидропривод». Основные этапы развития гидравлики как инженерной науки.
- •2. Физическое понятие жидкости как агрегатного состояния вещества.
- •3. Реальная и идеальная жидкость. Понятие вязкости.
- •4.1 Вязкость, как свойство жидкости.
- •4.2 Вязкость, как свойство жидкости.
- •5. Основные физические свойства реальных жидкостей.
- •6. Поверхностное натяжение. Капиллярный эффект.
- •7. Классификация сил, действующих на жидкость.
- •8.1 Свойства гидростатического давления.
- •8.2 Свойства гидростатического давления.
- •9. Уравнение равновесия покоящейся жидкости.
- •10. Основное уравнение гидростатики.
- •11. Понятие абсолютного и избыточного давления. Пьезометрическая высота. Вакуум.
- •12.1 Приборы для измерения давления.
- •12.2 Приборы для измерения давления.
- •13. Сообщающиеся сосуды. Закон Паскаля.
- •14.1 Относительный покой жидкости.
- •14.2 Относительный покой жидкости.
- •15. Поверхности равного давления.
- •16. Сила гидростатического давления, действующая на плоскую фигуру.
- •17. Определение положения центра давления на плоскую фигуру. Понятие эксцентриситета давления.
- •18. Сила гидростатического давления.
- •19. Построение эпюр гидростатического давления.
- •20. Закон Архимеда, плавание тел.
- •21. Линия тока, элементарная струйка.
- •22. Классификация видов движения жидкости.
- •23. Понятие расхода жидкости, средней скорости, живого сечения, гидравлического радиуса, смоченного периметра.
- •24. Дифференциальное уравнение неразрывности потока.
- •25. Дифференциальное уравнение движения идеальной жидкости.
- •26. Вывод уравнения Бернулли для идеальной жидкости.
- •27. Геометрическая и энергетическая интерпретация уравнения Бернулли.
- •28. Уравнение Бернулли для элементарной струйки реальной жидкости.
- •29. Уравнение Бернулли для потока реальной жидкости.
- •30.1 Пример использования уравнения Бернулли в технике.
- •30.2 Пример использования уравнения Бернулли в технике.
- •31. Понятие ламинарного и турбулентного режимов движения реальных жидкостей.
- •32. Критическое значение критерия Рейнольдса и его вывод.
- •33. Ламинарный режим движения. Распределение скорости жидкости по сечению потока.
- •34. Определение расхода жидкости и средней скорости ламинарного потока.
- •35. Понятие пульсационной, мгновенной, осредненной и средней скоростей течения.
- •36.1 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •36.2 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •37.1 Дифференциальное уравнение движения реальной жидкости Навье-Стокса.
- •39. Природа потерь напора, их связь с режимом движения жидкости.
- •40. Уравнение Дарси-Вейсбаха для расчета потерь напора по длине трубопровода.
- •41.1 Понятие гидравлически гладких и шероховатых труб.
- •41.2 Понятие гидравлически гладких и шероховатых труб.
- •42.1 Потери напора при турбулентном режиме движения.
- •42.2 Потери напора при турбулентном режиме движения.
- •43. Графики Никурадзе.
- •44.1 Условие возникновения местных потерь напора.
- •44.2 Условие возникновения местных потерь напора.
- •45. Резкое расширение трубопровода. Формула Борда.
- •46. Случаи местных сопротивлений, наиболее часто встречающиеся в инженерной практике.
- •47.1 Истечение жидкости через отверстие. Типы сжатия струи.
- •47.2 Истечение жидкости через отверстие. Типы сжатия струи.
- •48. Коэффициенты истечения и
- •49. Определение коэффициентов ипри истечении жидкости через малое и большое отверстие в тонкой стенке.
- •50. Определение коэффициентов ипри истечении жидкости через затопленное малое отверстие.
- •51. Истечение через насадки. Типы и применение насадков.
- •52.1 Истечение жидкости через внешний цилиндрический насадок.
- •52.2 Истечение жидкости через внешний цилиндрический насадок.
- •53. Истечение жидкости через отверстие при переменном напоре. Время опорожнения сосуда.
- •54. Классификация трубопроводов.
- •55.1 Гидравлический расчет простых трубопроводов.
- •55.2 Гидравлический расчет простых трубопроводов.
- •56 Характеристика трубопроводов. Кривые потребного напора.
- •57.1 Последовательное и параллельное соединение простых трубопроводов.
- •57.2 Последовательное и параллельное соединение простых трубопроводов.
- •58. Расчет разветвленного трубопровода.
- •59. Классификация насосов.
- •60. Принцип действия динамических насосов.
- •61. Основные характеристики насосов.
- •62.1 Устройство и принцип действия центробежного насоса.
- •62.2 Устройство и принцип действия центробежного насоса.
- •63. Движение жидкости в рабочем колесе центробежного насоса.
- •64. Основное уравнение центробежного насоса.
- •65.1 Характеристики центробежного насоса.
- •65.2 Характеристики центробежного насоса.
- •66. Законы пропорциональности для центробежных насосов.
- •67.1 Совместная работа насоса и трубопровода.
- •67.2 Совместная работа насоса и трубопровода.
- •68. Определение рабочей точки системы насос-трубопровод.
- •69.1 Регулирование подачи центробежных насосов.
- •69.2 Регулирование подачи центробежных насосов.
- •70.1 Последовательное и параллельное соединение насосов.
- •70.2 Последовательное и параллельное соединение насосов.
- •71. Общие сведения об объемных насосах.
- •72. Принцип действия объемных насосов.
- •73.1 Рабочие характеристики объемных насосов.
- •73.2 Рабочие характеристики объемных насосов.
- •74. Устройство и принцип действия поршневых насосов.
- •75. Роторные насосы.
- •76.1 Объемный гидропривод. Основные понятия и определения.
- •76.2 Объемный гидропривод. Основные понятия и определения.
- •77.1 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
- •77.2 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
33. Ламинарный режим движения. Распределение скорости жидкости по сечению потока.
При
ламинарном движении жидкости в
цилиндрической трубе распределение
скоростей по сечению имеет вид параболы
и схематически изображается телескопическим
(рис.): у стенок трубы скорости равны
нулю, а при удалении плавно возрастают
и достигают максимального значения на
оси трубы. Определим закон распределения
скоростей в живом сечении потока при
ламинарном режиме. Для этого выделим
внутри горизонтального трубопровода
объем жидкости в виде цилиндра радиусом
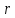 (рис.)
и длиной
(рис.)
и длиной
 и
составим уравнение равновесия всех
действующих сил:
и
составим уравнение равновесия всех
действующих сил:
 ,
где
,
где
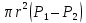 –
разность сил давления в сечениях 1 и 2;
–
разность сил давления в сечениях 1 и 2; –
сила трения на боковой поверхности
цилиндра. Знак минус в формуле Ньютона
взят потому, что градиент
–
сила трения на боковой поверхности
цилиндра. Знак минус в формуле Ньютона
взят потому, что градиент
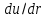 отрицателен,
поскольку с увеличением радиуса скорость
убывает. При равномерном движении
жидкости, при котором все живые сечения
по длине потока одинаковы как по форме,
так и по размерам, и скорости в
соответственных точках живых сечений
также одинаковы. Таким образом, скорость
является функцией исключительно одного
радиуса:
отрицателен,
поскольку с увеличением радиуса скорость
убывает. При равномерном движении
жидкости, при котором все живые сечения
по длине потока одинаковы как по форме,
так и по размерам, и скорости в
соответственных точках живых сечений
также одинаковы. Таким образом, скорость
является функцией исключительно одного
радиуса:
 C
учетом гидравлического уклона
C
учетом гидравлического уклона
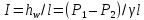 получим:
получим:
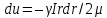 .
Интегрируя
по сечению трубы от
.
Интегрируя
по сечению трубы от
 до
до
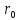 :
:
 учитывая,
что при
учитывая,
что при
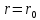 скорость
скорость
 ,
тогда
,
тогда ,
получим
закон распределения скоростей в живом
сечении потока:
,
получим
закон распределения скоростей в живом
сечении потока: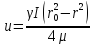
Для
центральной струйки при
 :
: .
Расход
жидкости через трубу при ламинарном
движении численно равен объему параболоида
скорости
.
Расход
жидкости через трубу при ламинарном
движении численно равен объему параболоида
скорости
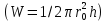 и
определяется из выражения
и
определяется из выражения
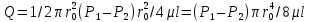 ,
отсюда
средняя скорость
,
отсюда
средняя скорость
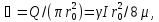 а
соотношение между максимальной и средней
скоростью
а
соотношение между максимальной и средней
скоростью
 Отсюда
закон распределения скоростей может
быть записан таким образом:
Отсюда
закон распределения скоростей может
быть записан таким образом:
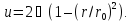
34. Определение расхода жидкости и средней скорости ламинарного потока.
Рассмотрим
движение вязкой жидкости в круглой
трубе радиусом R
при установившемся ламинарном режиме.
Выделяя в потоке цилиндрический объем
жидкости длиной
 и произвольным радиусом
и произвольным радиусом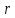 (рис.), из условия динамического равновесия
получим, что разность сил давления,
приложенных к выделенному объему в
сечениях 1-1 и 2-2, уравновешивается силами
трения, возникающими на его боковой
поверхности
(рис.), из условия динамического равновесия
получим, что разность сил давления,
приложенных к выделенному объему в
сечениях 1-1 и 2-2, уравновешивается силами
трения, возникающими на его боковой
поверхности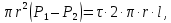 ,
где
,
где и
и
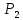 –давление
в центрах сечений 1-1 и 2-2. Из уравнения
энергетического баланса напоров для
рассматриваемого случая, следует, что
потери на трение по длине определяются
зависимостью
–давление
в центрах сечений 1-1 и 2-2. Из уравнения
энергетического баланса напоров для
рассматриваемого случая, следует, что
потери на трение по длине определяются
зависимостью Из выражения следует, что касательные
напряжения в сечении потока распределяются
линейно
Из выражения следует, что касательные
напряжения в сечении потока распределяются
линейно Решая
совместно (4) и (1), получаем дифференциальное
уравнение, определяющее скорость
Решая
совместно (4) и (1), получаем дифференциальное
уравнение, определяющее скорость
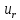 как функцию радиуса
как функцию радиуса
 :
: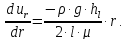 Интегрируя
уравнение с учетом граничного условия
(
Интегрируя
уравнение с учетом граничного условия
( при
при )
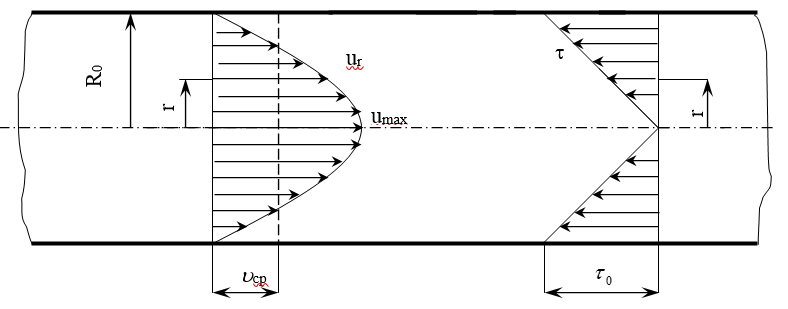
получаем параболический закон
распределения скоростей (рис.) по сечению
круглой трубы
)
получаем параболический закон
распределения скоростей (рис.) по сечению
круглой трубы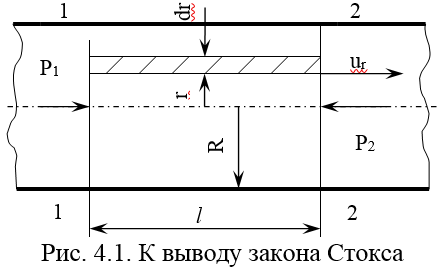
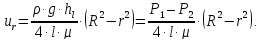 Скорость
имеет максимальное значение на оси
трубы, когда
Скорость
имеет максимальное значение на оси
трубы, когда
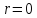 :
: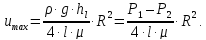 Сопоставляя
зависимости, находим закон Стокса,
выражающий параболическое распределение
скоростей в сечении трубопровода при
ламинарном движении
Сопоставляя
зависимости, находим закон Стокса,
выражающий параболическое распределение
скоростей в сечении трубопровода при
ламинарном движении
 Подсчитав
расход жидкости суммированием расходов
через элементарные кольцевые площадки
толщиной
Подсчитав
расход жидкости суммированием расходов
через элементарные кольцевые площадки
толщиной
 (рис.) сечения потока, находится средняя
скорость
(рис.) сечения потока, находится средняя
скорость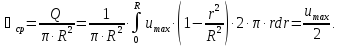 Отсюда
следует,
что средняя скорость потока при ламинарном
режиме равна половине максимальной.
Расход жидкости в круглой трубе при ее
ламинарном движении определяется
уравнением Пуазейля
Отсюда
следует,
что средняя скорость потока при ламинарном
режиме равна половине максимальной.
Расход жидкости в круглой трубе при ее
ламинарном движении определяется
уравнением Пуазейля
 где
где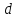 – внутренний диаметр трубы.
– внутренний диаметр трубы.
