- •1. Предмет курса «Гидравлика и гидропривод». Основные этапы развития гидравлики как инженерной науки.
- •2. Физическое понятие жидкости как агрегатного состояния вещества.
- •3. Реальная и идеальная жидкость. Понятие вязкости.
- •4.1 Вязкость, как свойство жидкости.
- •4.2 Вязкость, как свойство жидкости.
- •5. Основные физические свойства реальных жидкостей.
- •6. Поверхностное натяжение. Капиллярный эффект.
- •7. Классификация сил, действующих на жидкость.
- •8.1 Свойства гидростатического давления.
- •8.2 Свойства гидростатического давления.
- •9. Уравнение равновесия покоящейся жидкости.
- •10. Основное уравнение гидростатики.
- •11. Понятие абсолютного и избыточного давления. Пьезометрическая высота. Вакуум.
- •12.1 Приборы для измерения давления.
- •12.2 Приборы для измерения давления.
- •13. Сообщающиеся сосуды. Закон Паскаля.
- •14.1 Относительный покой жидкости.
- •14.2 Относительный покой жидкости.
- •15. Поверхности равного давления.
- •16. Сила гидростатического давления, действующая на плоскую фигуру.
- •17. Определение положения центра давления на плоскую фигуру. Понятие эксцентриситета давления.
- •18. Сила гидростатического давления.
- •19. Построение эпюр гидростатического давления.
- •20. Закон Архимеда, плавание тел.
- •21. Линия тока, элементарная струйка.
- •22. Классификация видов движения жидкости.
- •23. Понятие расхода жидкости, средней скорости, живого сечения, гидравлического радиуса, смоченного периметра.
- •24. Дифференциальное уравнение неразрывности потока.
- •25. Дифференциальное уравнение движения идеальной жидкости.
- •26. Вывод уравнения Бернулли для идеальной жидкости.
- •27. Геометрическая и энергетическая интерпретация уравнения Бернулли.
- •28. Уравнение Бернулли для элементарной струйки реальной жидкости.
- •29. Уравнение Бернулли для потока реальной жидкости.
- •30.1 Пример использования уравнения Бернулли в технике.
- •30.2 Пример использования уравнения Бернулли в технике.
- •31. Понятие ламинарного и турбулентного режимов движения реальных жидкостей.
- •32. Критическое значение критерия Рейнольдса и его вывод.
- •33. Ламинарный режим движения. Распределение скорости жидкости по сечению потока.
- •34. Определение расхода жидкости и средней скорости ламинарного потока.
- •35. Понятие пульсационной, мгновенной, осредненной и средней скоростей течения.
- •36.1 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •36.2 Закон внутреннего трения Ньютона. Гипотеза турбулентности Прандтля.
- •37.1 Дифференциальное уравнение движения реальной жидкости Навье-Стокса.
- •39. Природа потерь напора, их связь с режимом движения жидкости.
- •40. Уравнение Дарси-Вейсбаха для расчета потерь напора по длине трубопровода.
- •41.1 Понятие гидравлически гладких и шероховатых труб.
- •41.2 Понятие гидравлически гладких и шероховатых труб.
- •42.1 Потери напора при турбулентном режиме движения.
- •42.2 Потери напора при турбулентном режиме движения.
- •43. Графики Никурадзе.
- •44.1 Условие возникновения местных потерь напора.
- •44.2 Условие возникновения местных потерь напора.
- •45. Резкое расширение трубопровода. Формула Борда.
- •46. Случаи местных сопротивлений, наиболее часто встречающиеся в инженерной практике.
- •47.1 Истечение жидкости через отверстие. Типы сжатия струи.
- •47.2 Истечение жидкости через отверстие. Типы сжатия струи.
- •48. Коэффициенты истечения и
- •49. Определение коэффициентов ипри истечении жидкости через малое и большое отверстие в тонкой стенке.
- •50. Определение коэффициентов ипри истечении жидкости через затопленное малое отверстие.
- •51. Истечение через насадки. Типы и применение насадков.
- •52.1 Истечение жидкости через внешний цилиндрический насадок.
- •52.2 Истечение жидкости через внешний цилиндрический насадок.
- •53. Истечение жидкости через отверстие при переменном напоре. Время опорожнения сосуда.
- •54. Классификация трубопроводов.
- •55.1 Гидравлический расчет простых трубопроводов.
- •55.2 Гидравлический расчет простых трубопроводов.
- •56 Характеристика трубопроводов. Кривые потребного напора.
- •57.1 Последовательное и параллельное соединение простых трубопроводов.
- •57.2 Последовательное и параллельное соединение простых трубопроводов.
- •58. Расчет разветвленного трубопровода.
- •59. Классификация насосов.
- •60. Принцип действия динамических насосов.
- •61. Основные характеристики насосов.
- •62.1 Устройство и принцип действия центробежного насоса.
- •62.2 Устройство и принцип действия центробежного насоса.
- •63. Движение жидкости в рабочем колесе центробежного насоса.
- •64. Основное уравнение центробежного насоса.
- •65.1 Характеристики центробежного насоса.
- •65.2 Характеристики центробежного насоса.
- •66. Законы пропорциональности для центробежных насосов.
- •67.1 Совместная работа насоса и трубопровода.
- •67.2 Совместная работа насоса и трубопровода.
- •68. Определение рабочей точки системы насос-трубопровод.
- •69.1 Регулирование подачи центробежных насосов.
- •69.2 Регулирование подачи центробежных насосов.
- •70.1 Последовательное и параллельное соединение насосов.
- •70.2 Последовательное и параллельное соединение насосов.
- •71. Общие сведения об объемных насосах.
- •72. Принцип действия объемных насосов.
- •73.1 Рабочие характеристики объемных насосов.
- •73.2 Рабочие характеристики объемных насосов.
- •74. Устройство и принцип действия поршневых насосов.
- •75. Роторные насосы.
- •76.1 Объемный гидропривод. Основные понятия и определения.
- •76.2 Объемный гидропривод. Основные понятия и определения.
- •77.1 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
- •77.2 Гидролинии. Гидроемкости. Рабочие жидкости. Принципиальные схемы.
19. Построение эпюр гидростатического давления.
Избыточное
давление в любой точке смоченной
поверхности зависит от глубины погружения
данной точки и плотности жидкости, т.
е.
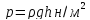 при условии, что давление на свободной
поверхности атмосферное. Если выбрать
масштаб
при условии, что давление на свободной
поверхности атмосферное. Если выбрать
масштаб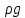 для воды равным единице, то давление в
каждой точке может быть выражено
вектором, равным величине высоты столбца
воды
для воды равным единице, то давление в
каждой точке может быть выражено
вектором, равным величине высоты столбца
воды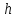 и направленным нормально к поверхности.
Таким образом, в случае плоских
вертикальных и наклонных поверхностей
масштаб
и направленным нормально к поверхности.
Таким образом, в случае плоских
вертикальных и наклонных поверхностей
масштаб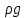 является угловым коэффициентом наклонной
прямой или тангенсом угла между ней и
высотой
является угловым коэффициентом наклонной
прямой или тангенсом угла между ней и
высотой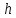 .
Для других жидкостей угловой коэффициент
выражается отношением
.
Для других жидкостей угловой коэффициент
выражается отношением – значений плотности. Следовательно,
каждый вектор представляет собой
давление, выраженное в метрах водяного
столба. Численное значение давления в
каждой точке поверхности может быть
получено умножением длины вектора,
выраженного в миллиметрах, на 9,81, так
как
– значений плотности. Следовательно,
каждый вектор представляет собой
давление, выраженное в метрах водяного
столба. Численное значение давления в
каждой точке поверхности может быть
получено умножением длины вектора,
выраженного в миллиметрах, на 9,81, так
как

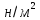 .
.
График распределения гидростатического давления по поверхности называется эпюрой давления.
На
(а) приведена эпюра избыточного давления
на плоское горизонтальное дно сосуда,
в который налита вода до уровня
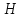 .
Т.к. все точки дна расположены на одной
глубине, то эпюра давления представляет
собой прямоугольник высотою
.
Т.к. все точки дна расположены на одной
глубине, то эпюра давления представляет
собой прямоугольник высотою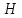 .На
(б) – эпюра избыточного давления на
плоскую вертикальную стенку сосуда, в
который до уровня
.На
(б) – эпюра избыточного давления на
плоскую вертикальную стенку сосуда, в
который до уровня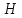 налита вода. На свободной поверхности
налита вода. На свободной поверхности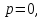 на дне сосуда
на дне сосуда
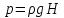 и в любом месте вертикальной стенки
давление определяется вектором
и в любом месте вертикальной стенки
давление определяется вектором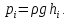 На
(в) – эпюра избыточного давления на
плоскую наклонную стенку, в точках 1 и
2 которой векторы давления соответственно
равны
На
(в) – эпюра избыточного давления на
плоскую наклонную стенку, в точках 1 и
2 которой векторы давления соответственно
равны
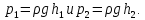 На
(г, д) – эпюры избыточных давлений на
криволинейные цилиндрические поверхности.
Давление в каждой точке поверхности
На
(г, д) – эпюры избыточных давлений на
криволинейные цилиндрические поверхности.
Давление в каждой точке поверхности
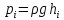 направлено нормально (по радиусу) к
поверхности.
направлено нормально (по радиусу) к
поверхности.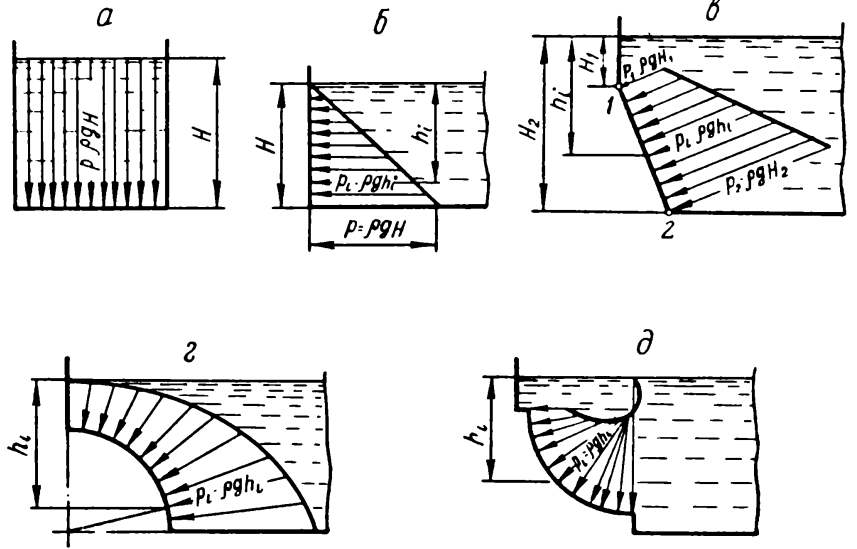
20. Закон Архимеда, плавание тел.
Тело,
полностью или частично погруженное в
жидкость, испытывает со стороны жидкости
суммарное давление, направленное
снизу-вверх и равное весу жидкости в
объеме погруженной части тела:
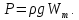 Иначе
говоря, на тело, погруженное в жидкость,
действует выталкивающая сила, равная
весу жидкости в объеме этого тела. Такая
сила называется Архимедовой силой, а
ее определение –законом
Архимеда.
Для однородного тела, плавающего на
поверхности справедливо соотношение:
Иначе
говоря, на тело, погруженное в жидкость,
действует выталкивающая сила, равная
весу жидкости в объеме этого тела. Такая
сила называется Архимедовой силой, а
ее определение –законом
Архимеда.
Для однородного тела, плавающего на
поверхности справедливо соотношение:
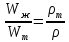 ,
где
,
где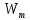 – объем плавающего тела;
– объем плавающего тела;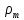 – плотность тела. Отношение плотности
плавающего тела и жидкости обратно
пропорционально отношению объема тела
и объема вытесненной им жидкости. В
теории плавания тел используются два
понятия: плавучесть и остойчивость.Плавучесть
– это способность тела плавать в
полупогруженном состоянии. Остойчивость
– способность плавающего тела
восстанавливать нарушенное равновесие
после устранения внешних сил (например,
ветра или крутого поворота), вызывающих
крен. Вес жидкости, судна взятой в объеме
погруженной части судна называют
водоизмещением, а точку приложения
равнодействующей давления (т.е. центр
давления) – центром водоизмещения. На
законе Архимеда основана теория плавания
тел. Центр водоизмещения не всегда
совпадает с центром тяжести тела
– плотность тела. Отношение плотности
плавающего тела и жидкости обратно
пропорционально отношению объема тела
и объема вытесненной им жидкости. В
теории плавания тел используются два
понятия: плавучесть и остойчивость.Плавучесть
– это способность тела плавать в
полупогруженном состоянии. Остойчивость
– способность плавающего тела
восстанавливать нарушенное равновесие
после устранения внешних сил (например,
ветра или крутого поворота), вызывающих
крен. Вес жидкости, судна взятой в объеме
погруженной части судна называют
водоизмещением, а точку приложения
равнодействующей давления (т.е. центр
давления) – центром водоизмещения. На
законе Архимеда основана теория плавания
тел. Центр водоизмещения не всегда
совпадает с центром тяжести тела
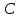 .
Если он выше центра тяжести, то судно
не опрокидывается. При нормальном
положении судна центр тяжести
.
Если он выше центра тяжести, то судно
не опрокидывается. При нормальном
положении судна центр тяжести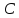 и центр водоизмещения
и центр водоизмещения лежат на одной вертикальной прямой
лежат на одной вертикальной прямой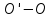 ,
представляющей ось симметрии судна и
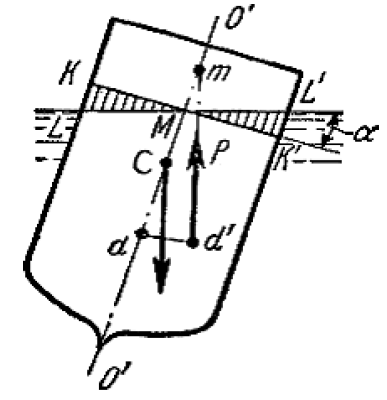
называемой осью плавания (рис.). Пусть
под влиянием внешних сил судно наклонилось
на некоторый угол
,
представляющей ось симметрии судна и
называемой осью плавания (рис.). Пусть
под влиянием внешних сил судно наклонилось
на некоторый угол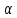 ,
часть судна
,
часть судна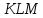 вышла из жидкости, а часть
вышла из жидкости, а часть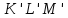 ,
наоборот, погрузилось в нее. При этом
получаем новое положение центра
водоизмещения –
,
наоборот, погрузилось в нее. При этом
получаем новое положение центра
водоизмещения –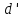 .
Приложим к точке
.
Приложим к точке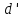 подъемную силу
подъемную силу и линию ее действия продолжим до
пересечения с осью симметрии
и линию ее действия продолжим до
пересечения с осью симметрии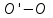 .
Полученная точка m называется метацентром,
а отрезок
.
Полученная точка m называется метацентром,
а отрезок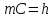 называетсяметацентрической
высотой.
Будем считать
называетсяметацентрической
высотой.
Будем считать
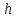 положительным, если точка m лежит выше
точки
положительным, если точка m лежит выше
точки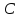 ,
и отрицательным – в противном случае.
Теперь рассмотрим условия равновесия
судна: если
,
и отрицательным – в противном случае.
Теперь рассмотрим условия равновесия
судна: если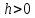 ,
то судно возвращается в первоначальное
положение; если
,
то судно возвращается в первоначальное
положение; если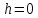 ,
то это случай безразличного равновесия;
если
,
то это случай безразличного равновесия;
если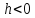 ,
то это случай неостойчивого равновесия,
при котором продолжается дальнейшее
опрокидывание судна. Следовательно,
чем ниже расположен центр тяжести и
больше метацентрическая высота, тем
больше будет остойчивость судна.
,
то это случай неостойчивого равновесия,
при котором продолжается дальнейшее
опрокидывание судна. Следовательно,
чем ниже расположен центр тяжести и
больше метацентрическая высота, тем
больше будет остойчивость судна.