Схемы алгоритмов и процедур:
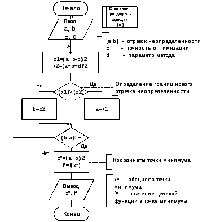
Рис. 6. Нахождение минимума методом дихотомии
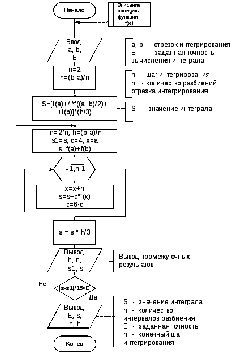
Рис. 7. Схема алгоритма интегрирования по методу Симпсона с использованием
правила Рунге
Тестирование и результаты тестирования:
Пример:
вычислить значение определенного
интеграла
,
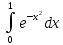предположив, что подынтегральная функция
задана таблично.
|
x |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
|
f(x) |
1.0 |
0.99005 |
0.960789 |
0.913913 |
0.852144 |
При использовании метода Симпсона, при ручном расчете должен получится
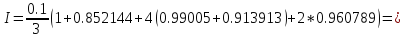0.37965
Проведем расчет в программе:
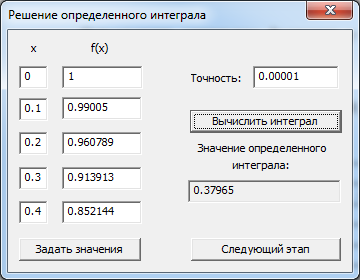
Рис. 8. по методу Симпсона с использованием правила Рунге
Теперь
протестируем метод нахождения минимума.
Возьмем простую функцию:
.
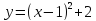Найдем минимум на промежутке[-1;4].
Решая
аналитическим методом найдем производную
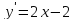и приравняем ее к нулю
,
,
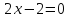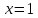подставим это значение в функцию и
получим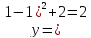
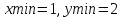
Проверим метод дихотомии:
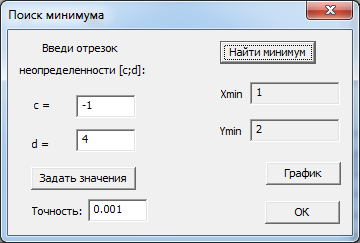
Рис. 9. Оптимизация методом дихотомии
Краткое описание используемых методов
В курсовой работе были использованы метод для нахождения минимума: метод дихотомии; метод для нахождения значения определенного интеграла: метод Симпсона.
Метод
дихотомии позволяют вычислить локальный
минимум функции с определенной точностью,
узнать необходимое количество итераций.
На каждой итерации при использовании
этого метода отрезок неопределенности
сокращается практически в два раза.
Конечная длина отрезка неопределенности
при использовании метода дихотомии
.
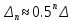Метод Рунге-Кутта 4-го порядка обладает очень высокой точностью, если применять его на относительно малом отрезе. Также этот метод является наиболее точным по сравнению с методом Эйлера и методом прогноза и коррекции.
Метод Симпсона для вычисления определенного интеграла - в этом методе используется три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид:
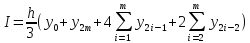
Литература
Гловацкая А.П., Загвоздкина А.В., Кравченко О.М., Семенова Т.И., Шакин В.Н., Практикум «Численные методы и оптимизация» по дисциплине «Информатика».
Учебное пособие-Раздел1-Инф(спецглавы)-210700
Лабораторный практикум-Раздел1-Инф(спецглавы)-210700
Основы работы с математическим пакетом Matlab. В.Н.Шакин, Т.И.Семенова