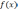Курсовая по ВМ - черновик
.docx
Московский технический университет связи и информатики
Курсовая работа по вычислительной математике
Кафедра вычислительной математики и программирования
Работу выполнил:
Студент ОТФ-2
группы БСТ1401
Балашов Иван, вариант 3
Работу проверила:
Семёнова Т.И.
Москва 2015
Определить
минимум функции 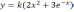
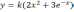 с
точностью
с
точностью 
 на отрезке
на отрезке 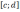
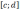
Параметр
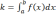
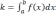 ,
функция
,
функция 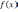
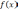 задана
таблично.
задана
таблично.
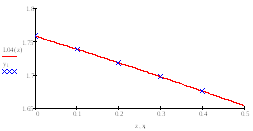
|
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
|
|
1.758203 |
1.738744 |
1.718369 |
1.697320 |
1.675834 |
|
|
|
|
|
|
|
|
|
|
|
|
Найти:
1)параметр


2)минимум
функции 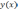
-
Постановка задачи
-
Описание используемых численных методов
-
Для интерполяции исходной таблично заданной функции будем использовать интерполяционный многочлен Лагранжа т.к.:
Общий вид интерполяционного многочлена Лагранжа:
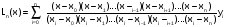
В исходной функции задано пять узлов, следовательно, будем использовать многочлен Лагранжа четвертой степени, имеющий вид:
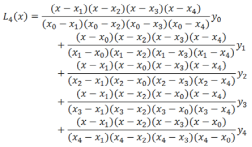
Решение:

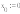
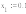
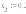
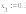
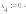
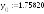
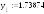
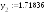
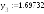
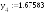
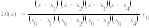
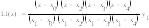
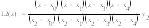
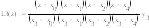
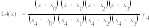
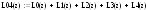

-
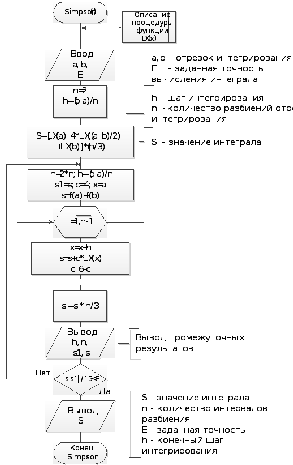
Для нахождения площади будем пользоваться формулой Симпсона.
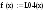

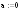
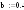
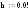
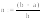
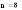

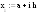
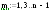
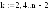
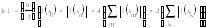

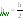
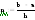
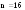

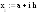
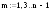
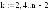
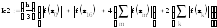

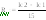
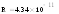
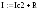
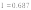
Решение:
-
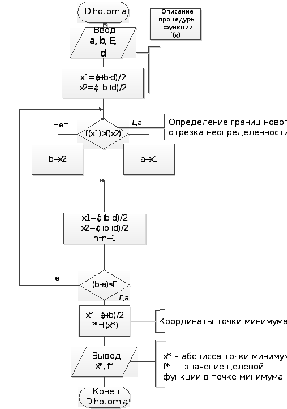
Для поиска минимума воспользуемся методом дихотомии.
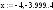
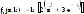
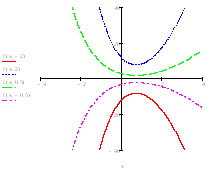
Как видно из графиков, если параметр k
принимает отрицательные значения, то
наша функция не имеет минимума и нам
необходимо решать обратную задачу,
нахождения максимума, следовательно,
у нас накладывается ограничение на
параметр k: 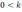
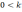 ,
в случае положительного kнеобходимо
выполнения условия нахождения одного
минимума на отрезке неопределённости:
,
в случае положительного kнеобходимо
выполнения условия нахождения одного
минимума на отрезке неопределённости:

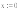
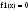

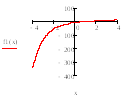
Как видно производная функции обращается в ноль только в одной точке, следовательно, функция имеет один глобальный максимум, и не требует дополнительного нахождения отрезка неопределённости. Длинна начального отрезка поиска минимума будет влиять только то, как быстро мы найдем минимум, но никак не повлияет на результат, и не приведет к ошибочным вычислениям
-
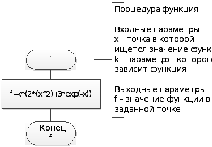
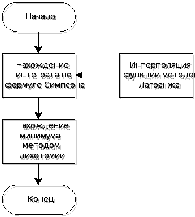
Схемы алгоритмов решения задачи
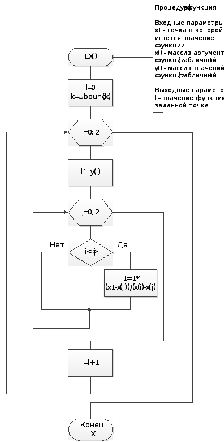
Данная процедура осуществляет вычисления значения полинома Лагранжа в заданной точке, и возвращает данное значение.
Данная процедура осуществляет подсчет интеграла по формуле Симпсона, на вход процедуре подается исходная функция, и границы нахождения интеграла.
Процедура нахождения минимума методом дихотомии
Процедура описывающая исходную функцию