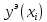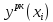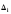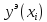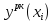Лабораторная работа 5 по ВМ
.docxМосковский Технический Университет
Связи и Информатики
Кафедра Информатики
ОТЧЕТ
по лабораторной работе № 5
«Методы решения обыкновенных дифференциальных уравнений»
Отчет подготовил:
студент группы БСТ1401
Балашов И.М.
Вариант № 3
Москва 2015
Задание
-
Выбрать индивидуальное задание в табл. 1.5-1 для решения обыкновенных дифференциальных уравнений:
-
дифференциальное уравнение
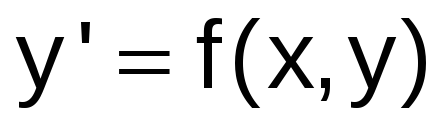 ;
;
-
интервал [a;b] , где ищется решение дифференциального уравнения;
-
начальные условия x0, y0;
-
шаг интегрирования h0.
-
Найти аналитическое решение
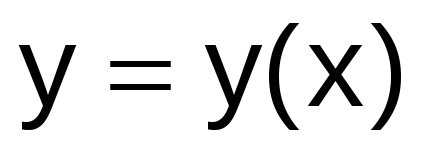 заданного дифференциального уравнения,
полагая его точным.
заданного дифференциального уравнения,
полагая его точным. -
Вычислить значения полученного решения
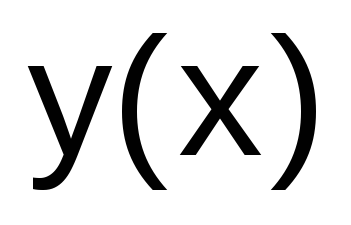 на отрезке [a;b]
с шагомh0.
на отрезке [a;b]
с шагомh0. -
Найти численное решение дифференциального уравнения методом Эйлера -
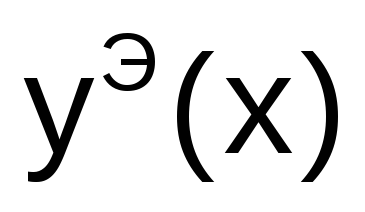 в точках отрезка [a;b]
с шагом h0
с помощью «ручного счета».
в точках отрезка [a;b]
с шагом h0
с помощью «ручного счета». -
Вычислить значения погрешностей
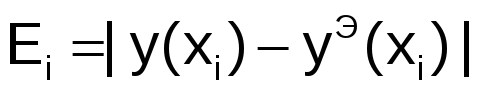 для
для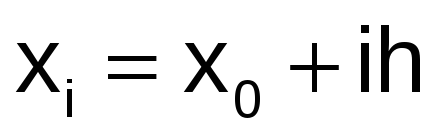 ,
,
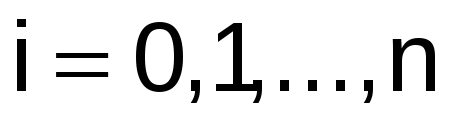 ,
,
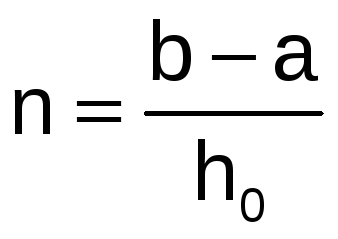 .
. -
Составить схему алгоритма, написать программу интегрирования дифференциальных уравнений методом Рунге-Кутты 4-го порядка с автоматическим выбором шага и провести контрольное тестирование на примере, рассмотренном в п. 1.5.5.
-
Получить решение«расчетом на ПК»
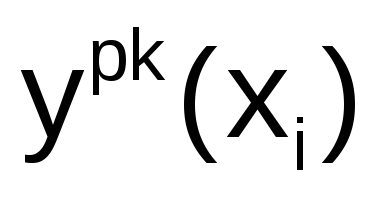 с шагом h0
и E
=10-4.
с шагом h0
и E
=10-4. -
Вычислить значения погрешностей
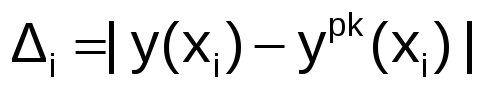 ,
,
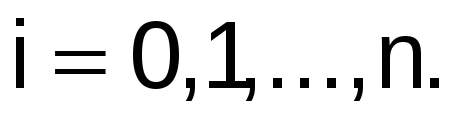
-
Графически проиллюстрировать решения
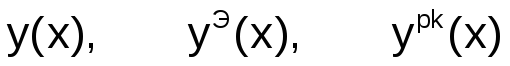 .
.
Индивидуальное задание:
|
№ вар |
Уравнение |
x0 |
y0 |
h0 |
a |
b |
|
3 |
y' = x3 y2 |
0 |
-2 |
0.2 |
0 |
2 |
Аналитическое решение
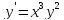
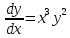
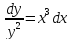
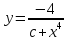
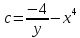
Из начальных условий следует, что c = 2.
Аналитическое решение дифференциального уравнения:
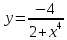
Значения точного решения ОДУ
С использованием Matlab
>> f = @(x,y)x.^3*y.^2;
>> [x,y]=ode23(f,0:0.2:2,-2)
x =
0
0.2000
0.4000
0.6000
0.8000
1.0000
1.2000
1.4000
1.6000
1.8000
2.0000
y =
-2.0000
-1.9985
-1.9750
-1.8786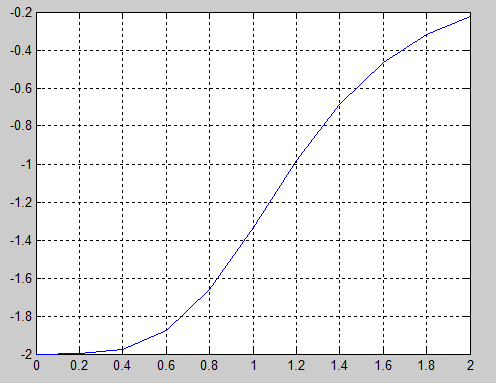
-1.6605
-1.3344
-0.9825
-0.6843
-0.4661
-0.3177
-0.2205
>> [x,y]=ode45(f,0:0.2:2,-2)
x =
0
0.2000
0.4000
0.6000
0.8000
1.0000
1.2000
1.4000
1.6000
1.8000
2.0000
y =
-2.0000
-1.9984
-1.9747
-1.8783
-1.6600
-1.3333
-0.9819
-0.6848
-0.4677
-0.3201
-0.2223
>> plot(x,y)
>> grid on
Ручной расчёт
|
xi |
y(xi) |
|
0 |
-2 |
|
0.2 |
-1.99840128 |
|
0.4 |
-1.97472354 |
|
0.6 |
-1.878287 |
|
0.8 |
-1.66002656 |
|
1 |
-1.33333333 |
|
1.2 |
-0.98193244 |
|
1.4 |
-0.68474391 |
|
1.6 |
-0.46763936 |
|
1.8 |
-0.32006145 |
|
2 |
-0.22222222 |
Численное решение заданного ДУ методом Эйлера
Найдем
значения численного решение ОДУ методом
Эйлера в точках отрезка [0;4] с шагом
h=0.4. Для этого ДУ записывают в виде
y’=f(x,y). Тогда общая формула для определения
очередного значения функции по методу
Эйлера имеет вид
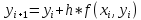
|
xi |
|
|
0 |
-2 |
|
0.2 |
-2 |
|
0.4 |
-1.9936 |
|
0.6 |
-1.94272716 |
|
0.8 |
-1.7796822 |
|
1 |
-1.45535388 |
|
1.2 |
-1.0317429 |
|
1.4 |
-0.66385398 |
|
1.6 |
-0.42199666 |
|
1.8 |
-0.27611256 |
|
2 |
-0.18718839 |
Значения погрешностей
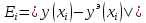
|
xi |
Ei |
|
0 |
0 |
|
0.2 |
0.00159872 |
|
0.4 |
0.01887646 |
|
0.6 |
0.06444016 |
|
0.8 |
0.11965564 |
|
1 |
0.12202055 |
|
1.2 |
0.04981046 |
|
1.4 |
0.02088993 |
|
1.6 |
0.0456427 |
|
1.8 |
0.04394889 |
|
2 |
0.03503383 |
Расчёт на ПК
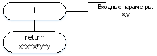
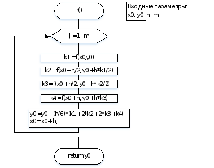
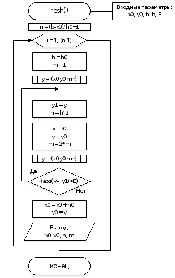
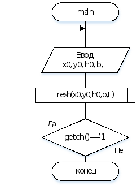
Код программы
#include<iostream>
#include <iomanip>
#include<conio.h>
#include<math.h>
using namespace std;
double f(double x, double y)
{
return x*x*x*y*y;
}
double r(double x0, double y0, double h, int m)
{
double k1, k2, k3, k4;
for(int j = 1; j <= m; j++)
{
k1 = f(x0,y0);
k2 = f(x0 + h/2, y0 + h*k1/2);
k3 = f(x0 + h/2, y0 + h*k2/2);
k4 = f(x0 + h, y0 + h*k3);
y0 = y0 + (h/6)*(k1 + 2*k2 + 2*k3 + k4);
x0 = x0 + h;
}
return y0;
}
void resh(double x0, double y0, double h0, double b, double E)
{
int m;
int n = (b - x0)/h0+1;
double h, x, y, y1;
for (int i = 1; i < n; i++)
{
h = h0;
m = 1;
y = r(x0,y0,h,m);
do
{
y1 = y;
h = h/2;
x = x0;
y = y0;
m = 2*m;
y = r(x0,y0,h,m);
} while (abs(y-y1)>E);
x0 = x0 + h0;
y0 = y;
cout << "x0 = "<< x0 <<"; "<<"y0 = "<<setprecision(8)<< y0 <<"; "<<"h = "<< h <<"; "<<"m = "<< m <<endl;
}
}
void main()
{
setlocale(0, "");
double x0, y0, h0, b, E;
int n;
do{
cout <<"Введите значениe x0:\n";
cin >> x0;
cout <<"Введите значениe y0:\n";
cin >> y0;
cout <<"Введите шаг h0:\n";
cin >> h0;
cout <<"Введите конец отрезка b:\n";
cin >> b;
cout <<"Введите погрешность E:\n";
cin >> E;
resh(x0, y0, h0, b, E);
cout <<endl<< "Для повторения нажмите '1'"<< endl;
}
while(getch()=='1');
}
Результат выполнения программы
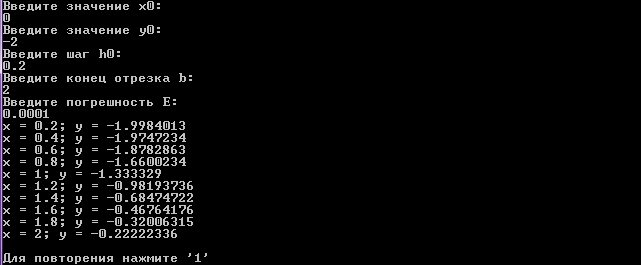
Решения, полученные по составленной программе «расчетом на ПК»
|
xi |
|
|
0 |
-2 |
|
0.2 |
-1.9984013 |
|
0.4 |
-1.9747234 |
|
0.6 |
-1.8782863 |
|
0.8 |
-1.6600234 |
|
1 |
-1.33329 |
|
1.2 |
-0.9819373 |
|
1.4 |
-0.6847472 |
|
1.6 |
-0.4676417 |
|
1.8 |
-0.3200631 |
|
2 |
-0.2222233 |
Значения погрешностей
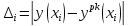
|
xi |
|
|
0 |
0 |
|
0.2 |
0.00000002 |
|
0.4 |
0.00000014 |
|
0.6 |
0.0000007 |
|
0.8 |
0.00000316 |
|
1 |
0.00004333 |
|
1.2 |
0.00000486 |
|
1.4 |
0.00000329 |
|
1.6 |
0.00000234 |
|
1.8 |
0.00000165 |
|
2 |
0.00000108 |
Все решения, полученные выше, сведем в табл. результатов 1.5-2:
|
xi |
y(xi) |
|
Ei |
|
|
|
0 |
-2 |
-2 |
0 |
-2 |
0 |
|
0.2 |
-1.99840128 |
-2 |
0.00159872 |
-1.9984013 |
0.00000002 |
|
0.4 |
-1.97472354 |
-1.9936 |
0.01887646 |
-1.9747234 |
0.00000014 |
|
0.6 |
-1.878287 |
-1.94272716 |
0.06444016 |
-1.8782863 |
0.0000007 |
|
0.8 |
-1.66002656 |
-1.7796822 |
0.11965564 |
-1.6600234 |
0.00000316 |
|
1 |
-1.33333333 |
-1.45535388 |
0.12202055 |
-1.33329 |
0.00004333 |
|
1.2 |
-0.98193244 |
-1.0317429 |
0.04981046 |
-0.9819373 |
0.00000486 |
|
1.4 |
-0.68474391 |
-0.66385398 |
0.02088993 |
-0.6847472 |
0.00000329 |
|
1.6 |
-0.46763936 |
-0.42199666 |
0.0456427 |
-0.4676417 |
0.00000234 |
|
1.8 |
-0.32006145 |
-0.27611256 |
0.04394889 |
-0.3200631 |
0.00000165 |
|
2 |
-0.22222222 |
-0.18718839 |
0.03503383 |
-0.2222233 |
0.00000108 |
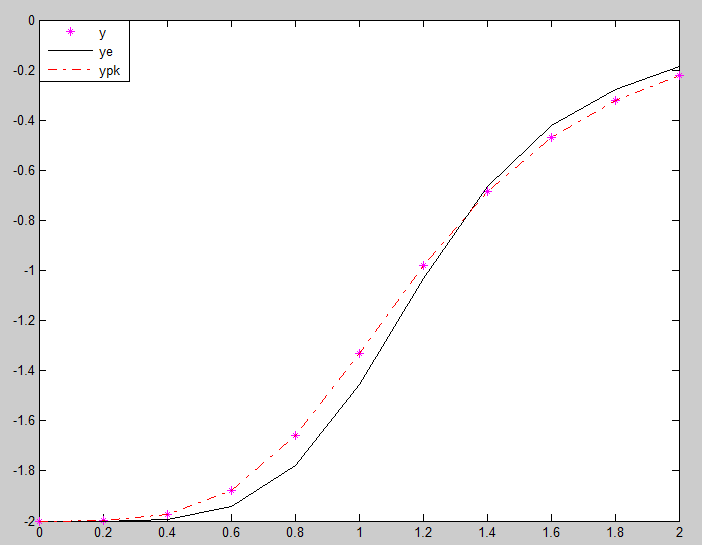
Графическая
иллюстрация решений
![]()