Московский Технический Университет

Связи и Информатики

Кафедра Информатики

ОТЧЕТ

по лабораторной работе №6

«Одномерная оптимизация»

Отчет подготовил:

студент группы БСТ1401

Балашов И.М.

Вариант № 3

Москва 2015

1. Выбрать индивидуальное задание по номеру варианта из табл. 1.6-1 для решения задачи одномерной оптимизации:

• функцию f(x),минимум которой необходимо найти;

• метод оптимизации для ручного расчета - значение параметра p;

• метод оптимизации для расчета на ПК - значение параметра t.

2. Провести исследование индивидуального варианта задания:

• построить график функции;

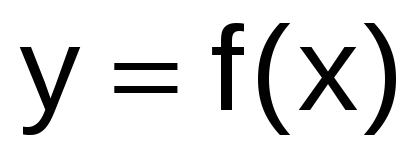• выбрать начальный отрезок неопределенности (отрезок, содержащий точку минимума);

• проверить выполнение аналитического условия унимодальности функции на выбранном отрезке.

3. Провести «ручной расчет» трех итерацийи определить длину отрезка, содержащего точку минимума, после трех итераций.

4. Составить схему алгоритма, написать программу решения задачи оптимизации

указанным в задании методом для «расчета на ПК» и провести контрольное тестирование программы, воспользовавшись исходными данными и результатами рассмотренного примера.

5. Решить задачу оптимизации с точностью E = 10^-4с помощь написанной программы («расчета на ПК»).

6. Вычислить число итераций, необходимых, чтобы локализовать точку минимума с

точностью E1 = 10^-4, расчет сравнить с результатом, полученным на ПК.

Индивидуальное задание

№ вар.	f(x)	t	p
3	sin(2x) – x	1	2

Расчёт на ПК - метод дихотомии

Ручной расчёт - метод золотого сечения

Исследование задания

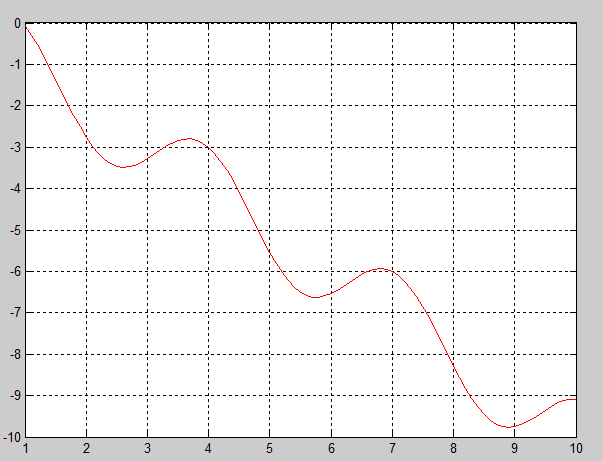
Выполнение задания с помощью Matlab

>> f = @(x)-cos(2.*x+1).*log(2./x)+3;

>> x = 1:0.1:10;

>> y = f(x);

>> plot(x,y,'r-')

>> grid on

>> syms z

>> ff = sin(2*z)-z;

>> diff(ff,z)

ans =

2*cos(2*z) - 1

>> diff(ff,z,2)

ans =

-4*sin(2*z)

>> x = 8:0.1:9;

>> t = [x;sin(2.*x)-x;2.*cos(2.*x) - 1;-4.*sin(2.*x)]

t =

8.0000 8.1000 8.2000 8.3000 8.4000 8.5000 8.6000 8.7000 8.8000 8.9000 9.0000

-8.2879 -8.5724 -8.8381 -9.0784 -9.2876 -9.4614 -9.5969 -9.6927 -9.7488 -9.7672 -9.7510

-2.9153 -2.7627 -2.5399 -2.2557 -1.9214 -1.5503 -1.1574 -0.7581 -0.3685 -0.0041 0.3206

1.1516 1.8897 2.5524 3.1134 3.5503 3.8456 3.9876 3.9706 3.7954 3.4688 3.0039

>> [x,y] =fminbnd(f,8,9)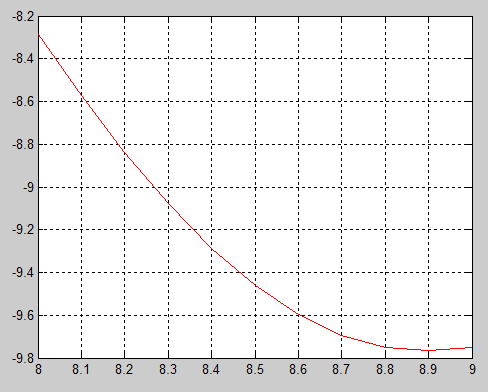

x =

8.9012

y =

-9.7672

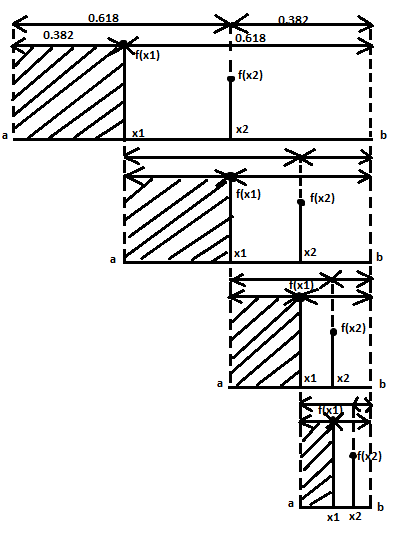
Ручной расчёт

Метод золотого сечения

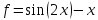
1 итерация:

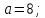
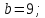
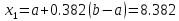
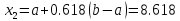
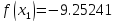
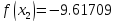
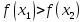
2 итерация:

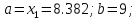
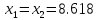
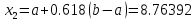
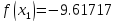
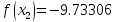
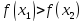
3 итерация:

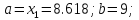
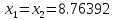
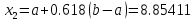
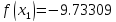
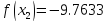
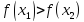
4 итерация:

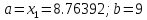
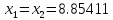
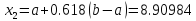
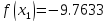
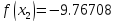
Результаты ручного расчёта

N	a	b	x1	x2	f(x1)	f(x2)
1	8	9	8.328	8.618	-9.25241	-9.61709	0.618
2	8.382	9	8.618	8.76392	-9.61818	-9.73306	0.38197
3	8.618	9	8.76392	8.85411	-9.73309	-9.7633	0.23607
4	8.76392	9	8.85411	8.90984	-9.7633	-9.76708	0.23603

Схема алгоритма. Программа. Результаты тестирования.

Схема алгоритма:

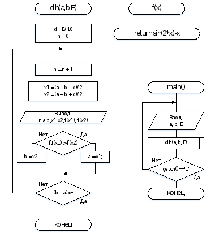
Код программы:

#include<iostream>

#include <iomanip>

#include<conio.h>

#include<math.h>

using namespace std;

double f(double x)

{

return -cos(2*x+1)*log(2/x)+3;

}

void dih(double a, double b, double E)

{

int n = 0;

double x1, x2;

double d = E/10;

do

{

n = n + 1;

x1 = (a + b - d)/2;

x2 = (a + b + d)/2;

cout <<"n = "<<n<<";["<<a<<";"<<b<<"]; x1 = "<<x1<<"; x2 = "<<x2<<";\nf(x1) = "<<f(x1)<<"; f(x2) = "<<f(x2)<<"\n\n";

if (f(x1) > f(x2))

a = x1;

else

b = x2;

} while ((b - a)>E);

}

void main()

{

setlocale(0, "");

double a, b, E;

do{

cout <<"Введите значениe a:\n";

cin >> a;

cout <<"Введите значениe b:\n";

cin >> b;

cout <<"Введите погрешность E:\n";

cin >> E;

dih(a, b, E);

cout <<endl<< "Для повторения нажмите '1'"<< endl;

}

while(getch()=='1');

}

Результат выполнения программы:

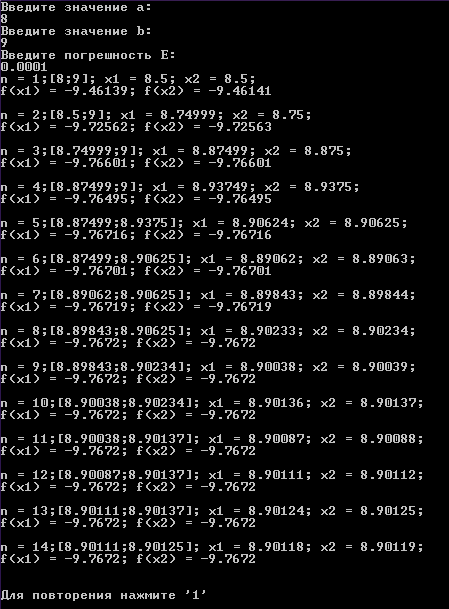
Результаты решения задачи оптимизации с помощью «расчета на ПК»

N	a	b	x1	x2	f(x1)	f(x2)
1	8	9	8.5	8.5	-9.46139	-9.46141	0.50001
2	8.5	9	8.74999	8.75	-9.72562	-9.72563	0.25002
3	8.74999	9	8.87499	8.875	-9.76601	-9.76601	0.12502
4	8.87499	9	8.93749	8.9375	-9.76495	-9.76495	0.06252
5	8.87499	8.9375	8.90624	8.90625	-9.76716	-9.76716	0.03127
6	8.87499	8.90625	8.89062	8.89063	-9.76701	-9.76701	0.01564
7	8.89062	8.90625	8.89843	8.89844	-9.76719	-9.76719	0.00783
8	8.89843	8.90625	8.90233	8.90234	-9.7672	-9.7672	0.00393
9	8.89843	8.90234	8.90038	8.90039	-9.7672	-9.7672	0.00197
10	8.90038	8.90234	8.90136	8.90137	-9.7672	-9.7672	0.00198
11	8.90038	8.90137	8.90087	8.90088	-9.7672	-9.7672	0.00100
12	8.90087	8.90137	8.90111	8.90112	-9.7672	-9.7672	0.00051
13	8.90111	8.90137	8.90124	8.90125	-9.7672	-9.7672	0.00027
14	8.90111	8.90125	8.90118	8.90119	-9.7672	-9.7672	0.00014

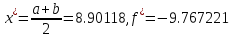
Число итераций, необходимых для локализации точки минимума и Е=10^-4

.

Если точность E =0.0001, а параметр метода d==0.00002, то получим:

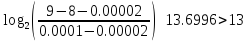
N = 14

Расчёт совпадает с теоретической оценкой.