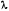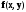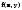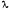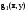Лабораторная работа 7 по ВМ
.docxМосковский Технический Университет
Связи и Информатики
Кафедра Информатики
ОТЧЕТ
по лабораторной работе №7
«Многомерная оптимизация»
Отчет подготовил:
студент группы БСТ1401
Балашов И.М.
Вариант № 3
Москва 2015
-
Выбрать индивидуальное задание из табл. 1.8-1 для решения задачи оптимизации функции нескольких переменных:
-
функцию–f(x, y);
-
метод оптимизации для «ручного расчета» – определяется значением параметра p;
-
метод оптимизации для «расчета на ПК»– значения параметровt и r.
-
Проверить условия существования точки минимума заданной функции f(x).
-
Решить задачу многомерной оптимизации аналитическим методом.
-
Выбрать начальную точкуx0, y0 итерационного процесса оптимизации.
-
Решить задачу оптимизации« ручным расчетом» (3 итерации)выбранным методом.
-
Вычислить погрешности
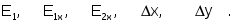
-
Составить схему алгоритма, программу решения задачи оптимизации и провести контрольное тестирование.
-
Решить задачу многомерной оптимизации «расчетом на ПК»при точности определения минимума E= 0.1, 0.05, 0.01, 0.001.
-
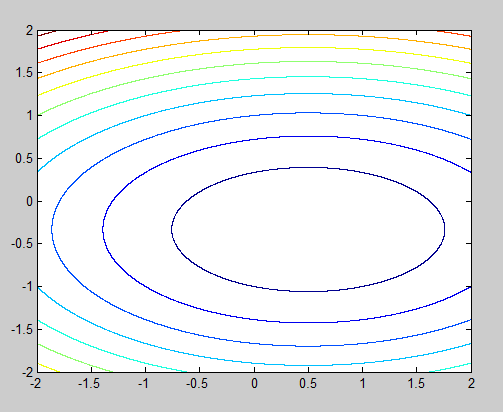
Построить траекторию поиска минимума по результатам«расчета на ПК» и изобразить схематически линии уровня, проходящие через точки траектории. На графике указать точку минимума, найденную в п. 3 задания.
Индивидуальное задание
|
№ |
Функция |
р |
t |
r |
|
3 |
3 x2 + y2 – 15 |
1 |
2 |
1 |
Ручной расчёт - метод ГДШ
Расчёт на ПК - метод НСЧ с подпрограммой метода золотого сечения
Проверка существования минимума функции
Матрица Гессе
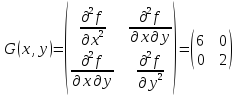
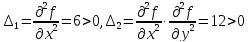
Таким
образом, функция
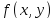 - выпуклая на множестве R.
- выпуклая на множестве R.
Решение задачи многомерной оптимизации аналитическим методом
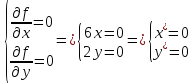
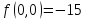
Начальная точка итерационного процесса численного решения задачи многомерной оптимизации
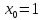
Решение задачи методом ГДШ «ручным расчетом»
Выполнение задания с помощью Matlab
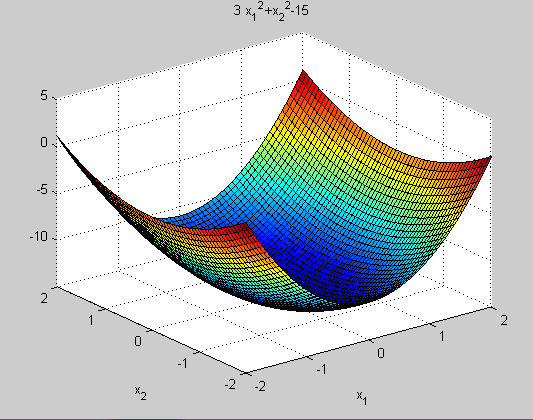
График функции
ezsurf('3.*x1.^2+x2.^2-15', [-2 2], [-2 2])
m-файл, целевая функция F(x)

Нахождение минимума функции
>> [X,Z] = fminsearch(@F,[0 1])
X =
0.0000 -0.4055
Z =
-15.0000
Ручной расчёт
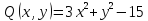
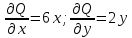
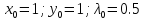
1 итерация
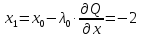
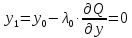
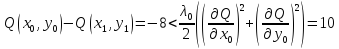
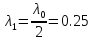
2 итерация
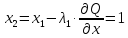
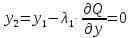
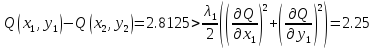
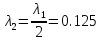
3 итерация
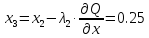
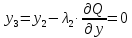
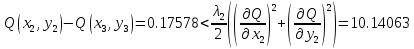
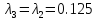
Результаты вычисления
|
k |
x |
y |
|
|
|
|
|
1 |
1 |
1 |
0.5 |
6 |
2 |
-11 |
|
2 |
-2 |
0 |
0.25 |
-12 |
0 |
-3 |
|
3 |
1 |
0 |
0.125 |
6 |
0 |
-12 |
|
4 |
0.25 |
0 |
0.0625 |
1.5 |
0 |
-14.8125 |
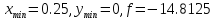
Погрешности после трех итераций
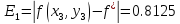
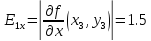
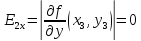
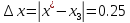
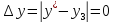
Схема алгоритма. Программа. Результаты контрольного тестирования.
Схема алгоритма
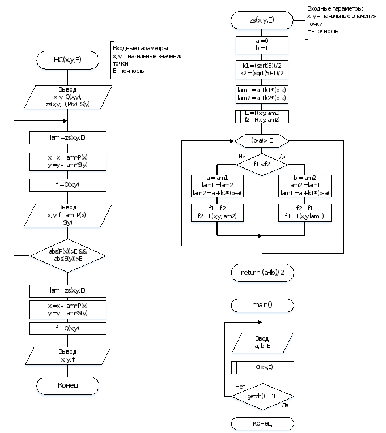
Код программы
#include<iostream>
#include<conio.h>
#include<math.h>
using namespace std;
double Q(double x, double y)
{
return 3*x*x+y*y-15;
}
double P(double x)
{
return 6*x;
}
double S(double y)
{
return 2*y;
}
double F(double x, double y, double lam)
{
return Q(x - lam * P(x),y - lam * S(y));
}
double zs(double x, double y, double E)
{
double k1, k2, lam, lam1, lam2, f1, f2;
double a = 0;
double b = 1;
k1 = (3-sqrt(5.0))/2;
k2 = (sqrt(5.0)-1)/2;
lam1 = a + k1*(b-a);
lam2 = a + k2*(b-a);
f1 = F(x, y, lam1);
f2 = F(x, y, lam2);
do
{
if (f1 < f2)
{
b = lam2;
lam2 = lam1;
lam1 = a + k1*(b - a);
f2 = f1;
f1 = F(x, y, lam1);
}
else
{
a = lam1;
lam1 = lam2;
lam2 = a + k2*(b - a);
f1 = f2;
f2 = F(x, y, lam2);
}
}while ((b - a) > E);
return (a + b)/2;
}
void HC(double x, double y, double E)
{
double lam, f;
cout<<"x = "<<x<<"; y = "<<y<<"; f(x,y) = "<<Q(x,y)<<"; lam = "<<zs(x,y,E)<<";\ng1 = "<<P(x)<<"; g2 = "<<S(y)<<"\n\n";
do
{
lam = zs(x,y,E);
x = x - lam*P(x);
y = y - lam*S(y);
f = Q(x,y);
cout<<"x = "<<x<<"; y = "<<y<<"; f(x,y) = "<<f<<"; lam = "<<lam<<";\ng1 = "<<P(x)<<"; g2 = "<<S(y)<<"\n\n";
}while((abs(P(x))>E) && (abs(S(y))>E));
lam = zs(x,y,E);
x = x - lam*P(x);
y = y - lam*S(y);
f = Q(x,y);
cout<<"x = "<<x<<"; y = "<<y<<"; f(x,y) = "<<f<<endl;
}
void main()
{
setlocale(0, "");
double x, y, E;
do{
cout<<"Введите x0:";
cin>>x;
cout<<"Введите y0:";
cin>>y;
cout<<"Введите погрешность E:";
cin>>E;
HC(x, y, E);
cout<<"\nДля повтора нажмите '1'\n";
}
while(getch()=='1');
}
Результаты выполнения программы
E = 0.1
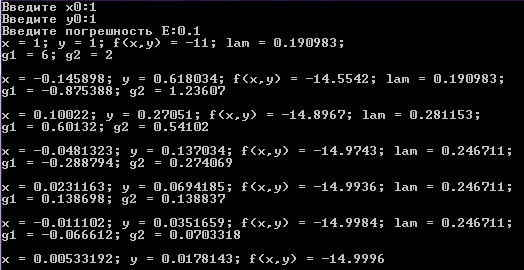
E = 0.5
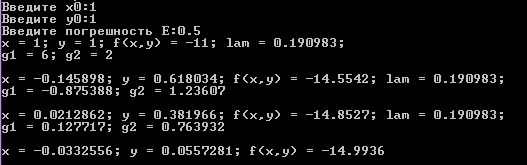
E = 0.01
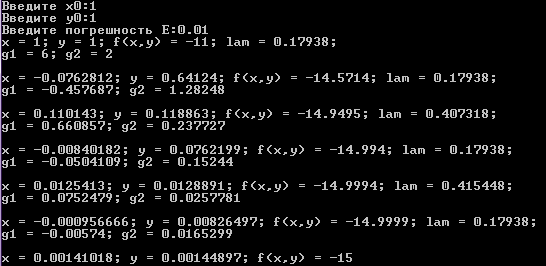
E = 0.001
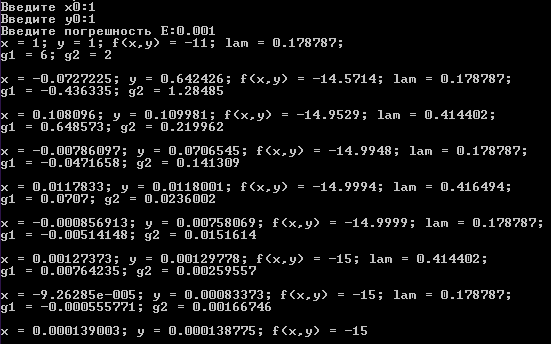
Решение задачи оптимизации на ПК
|
K |
E |
x |
y |
|
|
|
|
|
1 |
0.1 |
1 |
1 |
-11 |
0.190983 |
6 |
2 |
|
2 |
-0.14589 |
0.618034 |
-14.5542 |
0.190983 |
-0.875388 |
1.23607 |
|
|
3 |
0.10022 |
0.27051 |
-14.8967 |
0.281153 |
0.60132 |
0.54102 |
|
|
4 |
-0.04813 |
0.137034 |
-14.9763 |
0.246711 |
-0.288794 |
0.274069 |
|
|
5 |
0.231163 |
0.0694185 |
-14.9936 |
0.246711 |
0.138698 |
0.138837 |
|
|
6 |
-0.0111 |
0.0351659 |
-14.9984 |
0.246711 |
-0.066612 |
0.0703318 |
|
|
|
0.0053319 |
0.17814 |
-14.9996 |
|
|
|
|
|
1 |
0.05 |
1 |
1 |
-11 |
0.190983 |
6 |
2 |
|
2 |
-0.14589 |
0.618034 |
-14.5542 |
0.190983 |
-0.875388 |
1.23607 |
|
|
3 |
0.0212862 |
0.381966 |
-14.8527 |
0.190983 |
0.127717 |
0.763932 |
|
|
|
-0.033255 |
0.0557281 |
-14.9936 |
|
|
|
|
|
1 |
0.01 |
1 |
1 |
-11 |
0.17938 |
6 |
2 |
|
2 |
-0.14589 |
0.618034 |
-14.5542 |
0.17938 |
-0.875388 |
1.23607 |
|
|
3 |
0.10022 |
0.27051 |
-14.8967 |
0.407318 |
0.60132 |
0.54102 |
|
|
4 |
-0.04813 |
0.137034 |
-14.9763 |
0.17938 |
-0.288794 |
0.274069 |
|
|
5 |
0.231163 |
0.0694185 |
-14.9936 |
0.415448 |
0.138698 |
0.138837 |
|
|
6 |
-0.00095 |
0.008264 |
-14.9999 |
0.17938 |
-0.00574 |
0.0165299 |
|
|
|
0.00141 |
0.001448 |
-15 |
|
|
|
|
|
1 |
0.001 |
1 |
1 |
-11 |
0.17938 |
6 |
2 |
|
2 |
-0.14589 |
0.618034 |
-14.5542 |
0.17938 |
-0.875388 |
1.23607 |
|
|
3 |
0.10022 |
0.27051 |
-14.8967 |
0.407318 |
0.60132 |
0.54102 |
|
|
4 |
-0.04813 |
0.137034 |
-14.9763 |
0.17938 |
-0.288794 |
0.274069 |
|
|
5 |
0.231163 |
0.0694185 |
-14.9936 |
0.415448 |
0.138698 |
0.138837 |
|
|
6 |
-0.00095 |
0.008264 |
-14.9999 |
0.17938 |
-0.00574 |
0.0165299 |
|
|
7 |
0.00127 |
0.00129 |
-15 |
0.414402 |
0.00764 |
0.00259 |
|
|
8 |
-0.000009 |
0.00083 |
-15 |
0.178787 |
-0.00055 |
0.00166 |
|
|
|
0.000139 |
0.000138 |
-15 |
|
|
|
Координаты точки минимума и значения функции, вычисленные с точностью Е:
|
Метод |
E |
k |
x |
y |
f(x,y) |
|
НСЧ |
0.1 |
6 |
0.00533 |
0.17814 |
-14.999 |
|
0.05 |
3 |
-0.033255 |
0.05572 |
-14.9936 |
|
|
0.01 |
6 |
0.00141 |
0.001448 |
-15 |
|
|
0.001 |
8 |
0.000139 |
0.000138 |
-15 |
Траектория поиска минимума