Решение путем программирования.
Для решения поставленной задачи можно использовать метод дихотомии и метод золотого сечения. Я использую метод дихотомии, так как это метод требует провести меньшее количества итераций, для обеспечения одной и той же точности.
При решение 2 этапа использовались функции:
double f(double k, double x)
функция
возвращает значение функции
при заданном x
и k;
double dihotom(HWND hDlg, double E, double k, double a, double b)
[a;b] – начальный отрезок неопределенности
E – точность
k
–
параметр k
для функции
Функции
работают соответственно по методу
дихотомии или золотого сечения и
вычисляют значении абсциссы точки
минимума
.
Так
же выводит промежуточные данные в
ListBox.
На рис. 4 показан результат работы программы.
Рис. 4. Поиск минимума методом дихотомии
На рис. 5 показаны результаты промежуточных расчетов метода дихотомии:
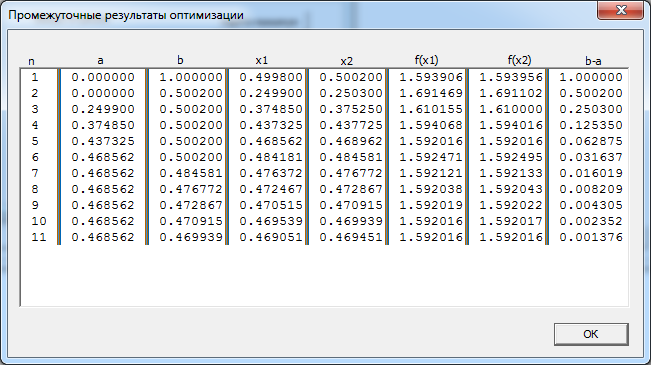
Рис. 5. Промежуточные результаты поиска минимума
Итог:
x = 0.4692 y = 1.5919 (MATLAB)
x = 0.46901 y = 1.592 (метод дихотомии с точностью 0.001)
Выводы по этапу:
На
данном этапе с помощью программы я нашел
значение точки минимума функции
с точностьюE
= 0.001.
Координаты точки минимума, найденные
с помощью программы, отличается от
значений, полученного с помощью
математического пакета, на величине,
которая меньше чем заданная точность.
Выводы по курсовой работе.
В
ходе выполнения курсовой работы,
производился поиск минимума функции
,
для чего был использован метод дихотомии.
Также, для вычисления параметра k, который представлял из себя определенный интеграл от таблично заданной функции, использовался метод Симпсона.
Все алгоритмы реализуются на C++. Курсовая работа разделена на два этапа: вычисление определенного интеграла и нахождение точки минимума. Программа полностью выполняет поставленную задачу, результаты сходятся с результатами из математического пакета MatLab.
Программа рассчитана на решение конкретной задачи, однако алгоритмы нахождения минимума и расчета определенного интеграла протестированы и на сторонних значениях, с заранее известными результатами при конкретных данных. Исходные данные и результаты взяты из методических материалов, указанных в списке литературы. Тестирования подтверждают верность работы всех алгоритмов.
Приложение. Код проекта: Файл my.H:
#pragma once
#include "resource.h"
#include <conio.h>
#include <iostream>
#include <math.h>
using namespace std;
#pragma warning(disable:4996)
double simpson(HWND hDlg, double E, double x1, double x2, double x3, double x4, double x5,
double fx1, double fx2, double fx3, double fx4, double fx5);
double dihotom(HWND hDlg, double E, double k, double a, double b);
Файл интеграл.Cpp:
#include "stdafx.h"
#include "my.h"
double simpson(HWND hDlg, double E, double x1, double x2, double x3, double x4, double x5,
double fx1, double fx2, double fx3, double fx4, double fx5) // решение интеграла по методу симпсона
{
int size = 5; // количество точек
double x[5] = { x1, x2, x3, x4, x5 }; // значения x
double fx[5] = { fx1, fx2, fx3, fx4, fx5 }; // значения функции f(x)
int a = 0, b = size - 1; // границы интегрирования
int n = 2; // количество разбиений отрезка интегрирования
double h = (x[b] - x[a]) / n; // шаг интегрирования
double s = (fx[a] + 4 * fx[b / 2] + fx[b]) * (h / 3), s1; // значение интеграла
int c;
do
{
n = 2 * n;
h = (x[b] - x[a]) / n;
s1 = s;
c = 4;
x1 = x[a];
s = fx[a] + fx[b];
for (int i = (size - 1) / n; i <= (size - 1) - (size - 1) / n; i++)
{
x1 += h;
s = s + c * fx[i];
c = 6 - c;
}
s = s * h / 3;
} while (abs(s - s1) / 15 > E); // дошли до указанной точности?
TCHAR I[20];
swprintf(I, TEXT("%.5g"), s);
SetDlgItemText(hDlg, IDC_ZNACHINTEG, I);
return s;}