ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФИССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ (МТУСИ)

Кафедра информатики

Курсовая работа по дисциплине: Информатика

Вариант № 211

Выполнил: студент группы БСТ 1402

ОТФ-2

Балашов Иван Михайлович

Проверила: Семёнова Татьяна Игоревна

Москва 2015 г.

Оглавление

Задание. 2

Схема алгоритма (перечисление этапов выполнения) 3

Описание хода выполнения курсовой работы. 4

Первый этап. 4

Решение в MATLAB: 4

Решение путем программирования: 4

Выводы по этапу: 5

Второй этап. 5

Решение в MATLAB. 5

Решение путем программирования. 7

Выводы по этапу: 9

Выводы по курсовой работе. 9

Приложение. 9

Код проекта: 9

Файл my.h: 9

Файл интеграл.cpp: 10

Файл оптимизация.cpp: 10

Файл курсовая.сpp: 11

Схемы алгоритмов и процедур: 17

Тестирование и результаты тестирования: 19

Краткое описание используемых методов 20

Литература 21

Задание.

Определить минимум функции 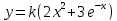с точностью E на отрезке [c; d].

Параметр , функция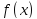задана таблично.

Исходные данные:

x	0	0.1	0.2	0.3	0.4
f(x)	1.758203	1.738744	1.718369	1.697320	1.675834

a	b	c	D	E
0	0.4	0	1	0.001

Схема алгоритма (перечисление этапов выполнения)

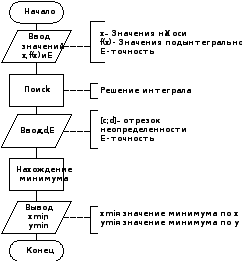
Рис. 1. Схема алгоритма (перечисление этапов выполнения)

Описание хода выполнения курсовой работы. Первый этап.

Название: «Решение интеграла».

Цель этапа: решение определенного интеграла таблично заданной функции.

Решение в matlab:

>> x = 0:0.1:0.4;

>> fx = [1.758203 1.738744 1.718369 1.697320 1.675834];

>> a = 0;

>> b = 0.4;

>> trapz(x, fx)

ans =

0.6871

Решение путем программирования:

Для решения поставленной задачи можно использовать методы прямоугольников, трапеций или Симпсона. Я выбрал формулу Симпсона, так как, анализируя значения погрешностей при выполнении лабораторной работы «Численное интегрирование», она обеспечила самый точный результат.

При решение 1 этапа использовалась функция:

• double simpson(HWND hDlg, double E, double x1, double x2, double x3, double x4, double x5, double fx1, double fx2, double fx3, double fx4, double fx5)

Функция работает по формуле Симпсона и вычисляет значение интеграла, с заданной точностью.

На рис. 2 показан результат работы программы:

Рис. 2. Решение интеграла по формуле Симпсона

Итог:

k = 0.6871 (MATLAB)

k = 0.68716 (методом Симпсона с точностью 0.001)

Выводы по этапу:

С помощью программы я нашел значение определенного интеграла таблично заданной функции с точностью E=0.001. Значение параметра k, найденного с помощью программы, отличается от значения, полученного с помощью математического пакета, на величине, которая меньше чем заданная точность.

Второй этап.

Название этапа: «Точка минимума».

Цель этапа: Найти абсциссу точки минимума функции 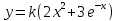на отрезке [0,1].

Решение в MATLAB.

Убедимся, что минимум функци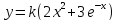и на отрезке [0,1] существует и, что он единственный.

>> f=@(x)(0.6871*(2*x.^2+3*exp(-x)));

>> x=0:0.001:1;

>> y=f(x);

>> plot(x,y,'r-')

>> grid on

Рис. 3. График функции

Из графика следует, что на отрезке [0;1] имеется локальный минимум. Исследуем функцию и поведение производных.

>> syms z;

>> ff=0.6871*(2*z.^2+3*exp(-z));

>> diff(ff,z)

ans =

(6871*z)/2500 - (20613*exp(-z))/10000

>> diff(ff,z,2)

ans =

(20613*exp(-z))/10000 + 6871/2500

>> x=0:0.2:1;

>> t=[x;0.6871*(2*x.^2+3*exp(-x));(6871*x)/2500 - (20613*exp(-x))./10000;(20613*exp(-x))./10000 + 6871/2500]

t =

0 0.2000 0.4000 0.6000 0.8000 1.0000

2.0613 1.7426 1.6016 1.6260 1.8057 2.1325

-2.0613 -1.1380 -0.2824 0.5178 1.2725 1.9901

4.8097 4.4360 4.1301 3.8797 3.6746 3.5067

0	2.0613	-2.0613	4.8097
0.2	1.7426	-1.138	4.4360
0.4	1.6016	-0.2824	4.1301
0.6	1.626	0.5178	3.8797
0.8	1.8057	1.2725	3.6746
1	2.1325	1.9901	3.5067

Так как не убывающая ина отрезке [0;1] существует единственный минимум.

Координаты минимума:

>> [x,y] = fminbnd(f,0,1)

x =

0.4692

y =

1.5919