Добавил:

ota Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тольяттинский государственный университет

Предмет:

Высшая математика

Файл:

высшая математика руководство к решению задач часть 3.pdf

Скачиваний:

2569

Добавлен:

26.07.2016

Размер:

835.31 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

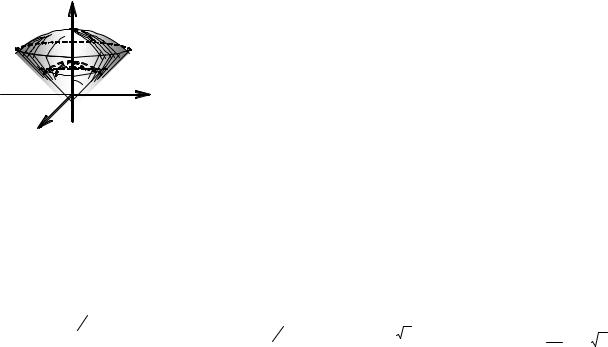
Пример 4. Найти объём тела, ограниченного поверхностями

x 2 + y 2 + z2 = 16, x 2 + y 2 + z2 = 4, x 2 + y 2 = z2 (z > 0, x 2 + y 2 ≤ z2 ).

Решение. Данное тело расположено внутри конуса между двумя сферами радиусов 2 и 4

z		Проведём вычисления в сферической системе координат:
4		x = r cosϕsinθ, y = r sinϕ sinθ,
2		z = rcosθ, \|I\| = r2sinθ.
2		Запишем уравнения поверхностей:
θ		Запишем уравнения поверхностей:
θ	y	r 2 cos2 ϕ sin 2 θ + r 2 sin 2 ϕ sin 2 θ +
0	y	r 2 cos2 ϕ sin 2 θ + r 2 sin 2 ϕ sin 2 θ +
x		+ r 2 cos2 θ = 16,
		r 2 [sin 2 θ(cos2 ϕ + sin 2 ϕ)+ cos2 θ] = 16,
		r2 = 16 ρ = 4 – уравнение внешней сферы, аналогично

уравнение внутренней сферы: r = 2. Уравнение конуса

r 2 (cos2 ϕ sin 2 θ + sin 2 ϕ sin 2 θ) = r 2 cos2 θ, sin 2 θ = cos2 θ,

т. к. по условию объём находится внутри верхней части конуса (z ≥ 0), то tgθ = 1, (sinθ = cosθ), 0 ≤ θ ≤ π/4.

Итак,

2π	π 4	4	2		2π	π		ρ3		4		2		1			56	(2 − 2 ).

V = ∫ dϕ ∫ dθ∫ r				sin θdr = ϕ	0	[− cos θ]0	4	3			= = 2π −		+ 1		(64	− 8) = π	3
												2		3
0	0	2							2

Задачи

1. Вычислить интеграл∫∫∫ xydxdydz преобразовав его к сферическим координатам, если

область V, ограничена поверхностями x2 + y 2 + z 2 = 9 , x2 + y 2 = z 2 (внутри конуса).

Приложение двойных и тройных интегралов

Цель: приложение тройных и двойных интегралов к задачам механики.

Аудиторная работа Приложение двойного интеграла к задачам механики и геометрии

Если D – плоская пластинка, лежащая в плоскости XOY с поверхностной плотностью μ = μ (x, y) , то ее массу находят по формуле

m = ∫∫μ (x, y)dxdy ,

а координаты центра тяжести xc и yc пластинки находят по формулам

xc =	∫∫ xμ (x, y)dxdy	; yc =	∫∫ yμ (x, y)dxdy
	D		D	,
	∫∫μ (x, y)dxdy		∫∫μ (x, y)dxdy	,
	∫∫μ (x, y)dxdy		∫∫μ (x, y)dxdy
	D		D

где ∫∫ xμ (x, y)dxdy - статический момент пластинки относительно оси OY; ∫∫ yμ (x, y)dxdy

	D				D
- статический момент пластинки относительно оси OX, а для однородных пластинок
xc =		∫∫ xdxdy	, yc =	∫∫ ydxdy
		D		D	,
		∫∫dxdy		∫∫dxdy	,
		∫∫dxdy		∫∫dxdy
		D		D

где ∫∫dxdy - площадь области D.

Объем цилиндрического тела, ограниченного сверху поверхностью z = f (x, y), а снизу -

областью D, находится по формуле

V = ∫∫ f (x, y)dxdy.

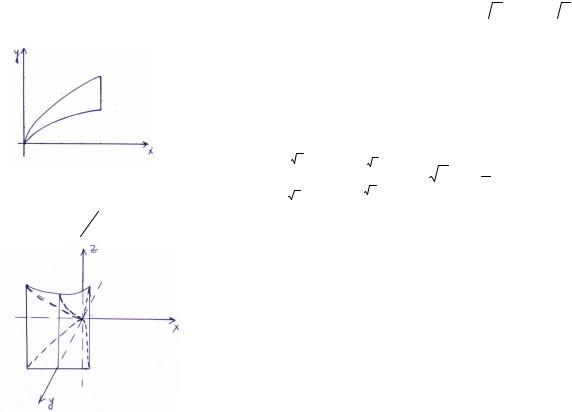
Пример 1. Вычислить площадь области D, ограниченной линиями y = x ; y = 2 x ; x- 4=0.

Решение.

Построив данные линии, получим область D, простую относительно OX, тогда

	4	2 x		4	2 x	4	2		3	4		2	3		16

S = ∫∫dxdy = ∫dx			∫dy = ∫ y		\| dx = ∫ xdx =			x 2 \|			=		4 2	=		.
							3					3			3
D	0		x	0	x	0		0

Ответ: S = 163 (кв.ед.).

Пример 2.

Вычислить объем тела, ограниченного поверхностями z=x2+y2; z=0; y=x2; y=1.

Решение.

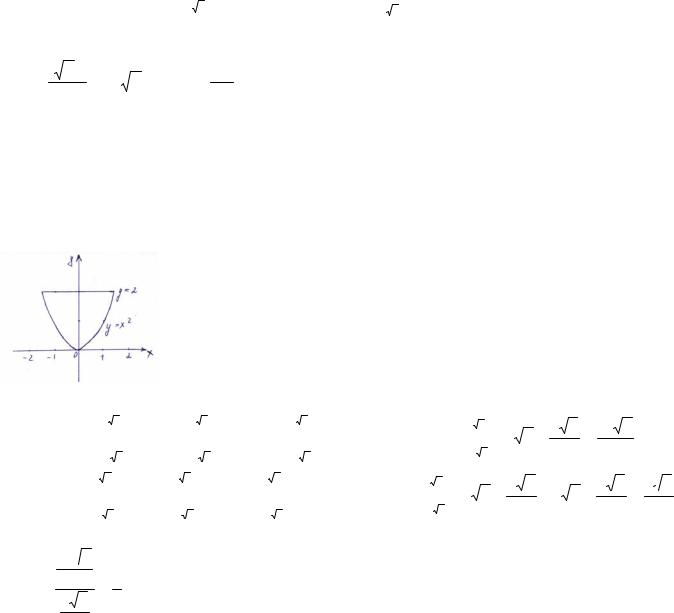
Построив поверхности, получим тело V, для которого плоскость YOZ – плоскость симметрии. На основании формулы V = ∫∫ f (x, y)dxdy,

												D
			(x2	+ y 2 )dxdy = 2				1		y	(x2 + y 2 )dx = 2		1	x	3		y
								1					1		3		y
V =	∫∫							∫	dy	∫						+ xy2	\| dy =
V =									dy							+ xy2	\| dy =
													∫	3
	D	( y )3						0		0			0	3		0
1		( y )3										88
= 2∫			3	+ y 2			y dy = ... =					88
			3									105
0
Ответ: V=						88	(куб.ед.).
Ответ: V=					105		(куб.ед.).
					105

Пример 3.

Найти координаты центра тяжести однородной пластины, ограниченной параболой y=x2 и y=2.

Решение.

Построив линии, ограничивающие пластину, замечаем, что пластина симметрична относительно оси OY. Следовательно, xc=0, а

∫∫ ydxdy

yc =	D	.
yc =	∫∫dxdy	.
	∫∫dxdy
	D

∫∫

∫

ydxdy =

ydy =

dx =

−

− 2

∫∫

dxdy =

2 dy =

2(2 − x2 )dx

∫

− 2

16 2

yc= 8 52 = 65 = 1,2 3

Ответ: xc=0; yc=1,2.

Задачи:

x4							x5		2				4 2		16 2
		dx =		2x −					\|	= 4 2		−		=
		dx =		2x −					\|	= 4 2		−		=
2							10						5		5
2							10	−	2				5		5
			x3			2					2 2				2 2
=	2x −					\|	=	2 2 −				+ 2 2 −				=
=	2x −					\|	=	2 2 −				+ 2 2 −				=
			3								3				3
			3		−	2					3				3

1.Вычислить объем тела, ограниченного поверхностями x2+y2=2x; z=2x; z=4x.

2.Вычислить координаты центра тяжести фигуры (однородной пластины), ограниченной

кривой y=sinx и прямой OA, проходящей через начало координат и точку А( π2 ;1).

8 2

Приложение тройных интегралов Основные формулы для тройных интегралов Центр тяжести тела

∫∫∫ xdxdydz

∫∫∫ ydxdydz

∫∫∫ zdxdydz

x =

, y =

, z =

∫∫∫dxdydz

Масса тела

m = ∫∫∫ ρ (x, y,z)dxdydz , где ρ = ρ (x, y,z)- плотность

Момент инерции тела относительно осей координат

Iox = ∫∫∫

(y 2 + z 2 )dxdydz , Ioy

= ∫∫∫

(x2

+ z 2 )dxdydz ,

Ioz

= ∫∫∫(y 2 + x2 )dxdydz

Момент инерции тела относительно начала координат

= ∫∫∫(x2 + y 2 + z 2 )dxdydz

Объем тела V = ∫∫∫ dxdydz

Пример 1 . Найти массу тела, ограниченного поверхностями z 2

= 6x ,

x = 2 , y = 0 ,

y = 1,

z = 0 , если плотность равна ρ (x, y,z) = z .

Проекция области V на плоскость XOY будет

прямоугольник ОАВС , поэтому пределы интегрирования бкдут

0 ≤ x ≤ 2

иметь вид 0 ≤ y ≤ 1

0 ≤ z ≤ 6x

По формуле m = ∫∫∫ ρ (x, y,z)dxdydz имеем

6 x

m = ∫∫∫ zdxdydz =∫ dx∫ dy ∫ zdz = ∫ dy

∫

= ∫ dy∫18x

dx =

0 2

∫

= ∫ 48dy = 48y

0 = 48

Пример 2. Найдем координаты центра тяжести однородного тела, ограниченного

цилиндром z =

y 2 и плоскостями y = 0 ,

z = 0 ,

x = 0 ,

2x + 3y − 12 = 0 .

Проекцией области V на плоскость XOY имеет вид

треугольника. Поэтому пределы интегрирования имеют вид:

0 ≤ x ≤ 6,0 ≤ y ≤ 4 −

x,0 ≤ z ≤

y 2 .

x =

∫∫∫ xdxdydz

, y =

∫∫∫ ydxdydz

Используя формулы

∫∫∫dxdydz

∫∫∫ zdxdydz

z = V∫∫∫dxdydz найдем центр тяжести.

																																																																																				4−			2		x
																					2				1 2												4−			2		x																	2															6		y3									3
															6				4−					x				y				6					3										1		y2		6					4−					x		1												∫ x																dx
															6				4−		3			x	2			y				6					3										1		y2		6					4−			3		x														∫ x																dx
						∫∫∫ xdxdydz									∫ xdx					∫ dy ∫ dz												∫ xdx							∫ dy z							02							∫ xdx					∫							y2dy									0								6	0
						∫∫∫ xdxdydz									∫ xdx					∫ dy ∫ dz												∫ xdx							∫ dy z							02							∫ xdx					∫							y2dy									0								6	0
x =					V								=		0					0								0		=		0					0														=		0					0					2										=																			=
x =													=							2					1					=									2												=							2															=																			=
							∫∫∫dxdydz											4−		2		x			1		y2									4−			2		x					1		y2							4−			2		x																							4−		2			x
							∫∫∫dxdydz											4−				x					y2									4−					x					1									4−					x																							4−					x
															6					3					2							6					3														6							3				1				2								6			y			3					3
															6					3					2							6					3														6							3				1				2								6						3					3
							V									∫ dx ∫ dy											∫ dz					∫ dx						∫ dy z								02							∫ dx				∫								y			dy							∫															dx
							V																																																							2

															0			0							0							0					0														0					0																		0				6				0

	1		6							2	3						6														16						8						3									32x		2	−	32					x		3	+			4			x	4		−		8				x5					6
	1		6							2	3						6														16						8						3											2		32							3				4				4				8				x5					6
				∫			4		−		x	xdx					∫	64 − 32x +															x −									x		xdx												3										3								27						5											6
				∫			4		−		x	xdx					∫	64 − 32x +															x −									x		xdx
=	6		0							3						=	0														3						27													=																																		0		=
	6		0							3							0														3						27																																															0
		1				6				2		3					1							3	6						2			3									2														3									2						4		1		6														5
						6																			6																																															4																		5


						∫		4 −			x			dx
		6				∫		4 −		3	x			dx						−				2		∫		4 −			3	x			d 4							−	3		x										−		2					4 −				3			x					4
		6				0				3							6							2	0						3												3														2									3								4		0
V = ∫∫∫ dxdydz = 96
							v
						∫∫∫ ydxdydz									2									∫∫∫ zdxdydz												8
y =					V									=	2		z =						V										=			8
y =									V					=	5		z =												V				=		5
									V						5														V						5
Задачи:
1.		Вычислить объем тела ограниченного поверхностями y = 0 ,																																																					z = 0 ,									x = 0 ,								x = 4 ,									y = 4 ,
z = x2		+ y 2							+ 1.

Ответ: 186 2 3

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
26.07.2016399.9 Кб101высшая математика пособие для академических консультантов часть 3.pdf
#
26.07.2016277.65 Кб60высшая математика пособие для преподавателя часть 3.pdf
#
26.07.2016478.99 Кб81высшая математика пособие для студентов часть 3.pdf
#
26.07.2016835.31 Кб2569высшая математика руководство к решению задач часть 3.pdf
#
26.07.2016564.19 Кб158высшая математика Ряды-1.pdf
#
26.07.2016564.19 Кб103высшая математика Ряды.pdf
#
26.07.2016178.67 Кб20высшая математика структура дисциплины часть 3.pdf
#
26.07.2016113.73 Кб23высшая математика структура дисциплины часть 4.pdf
#
26.07.20161.43 Mб111высшая математика теоретический материал часть 3.pdf