Добавил:

ota Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тольяттинский государственный университет

Предмет:

Высшая математика

Файл:

высшая математика руководство к решению задач часть 3.pdf

Скачиваний:

2554

Добавлен:

26.07.2016

Размер:

835.31 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Модуль 10. Кратные интегралы

Понятие двойного интеграла. Вычисление двойного интеграла в декартовой системе координат

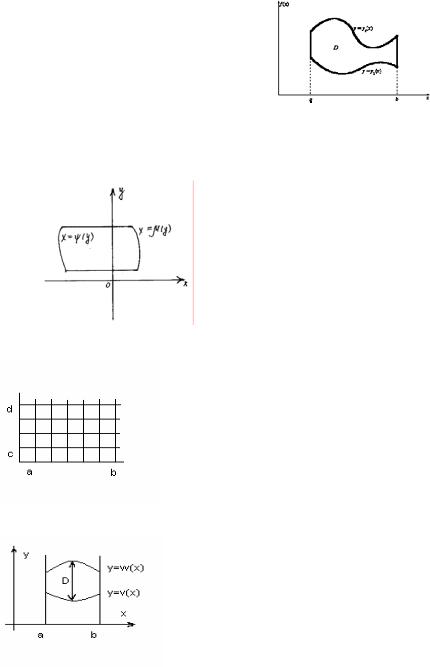
Определение. Будем считать область D простой относительно оси ОХ, если она ограничена сверху линией y = y2 (x), снизу линией y = y1 (x), где y1(x) и y2(x) – непрерывные

на отрезке [a,b], и с боков ограничена отрезками прямых x=a, x=b. В отдельных случаях отрезки прямых вырождаются в точки.

y = y1 (x)- линия входа в область;
y = y2 (x)- линия выхода из	области.

Определение. Область D простая относительно оси ОY, если она ограничена слева линией x = ψ (y), справа линией x = μ (y), сверху отрезком прямой y=d, а снизу отрезком прямой y=c (рис.).

Интеграл по прямоугольнику D.

Перестановка пределов интегрирования.

d b d b b d

∫∫ f (x, y)dxdy = ∫dy∫ f (x, y)dx = ∫dx∫ f (x, y)dy

c a c a a c

bw( x)

∫∫f (x, y)dxdy = ∫dx ∫ f (x, y)dy

(D)

a v( x)

Аудиторная работа

Вычисление двойных интегралов по прямоугольной области

Пример 1. Вычислить интеграл I = ∫∫ 2x 2 cos y3 dxdy , где область D : 1 ≤ x ≤ 2 , 0 ≤ y < 2π .

Решение. Поскольку область интегрирования прямоугольная, пределы интегрирования в двухкратном интеграле — постоян-ные, а т.к. подынтегральная функция есть произведение множителей, каждый из которых зависит только от одной переменной, то порядок интегрирования выбираем произвольно, например:

2	π 2	= 2	x3	2	[3 sin		]π 2		8 − 1	3(sin	π	− sin 0)= 7.
I = 2∫ x 2 dx ∫ cos y dy						y		= = 2
			3			3			3		6
	3			1			0
1	0

Самостоятельная работа

∫∫ f (x, y)dxdy

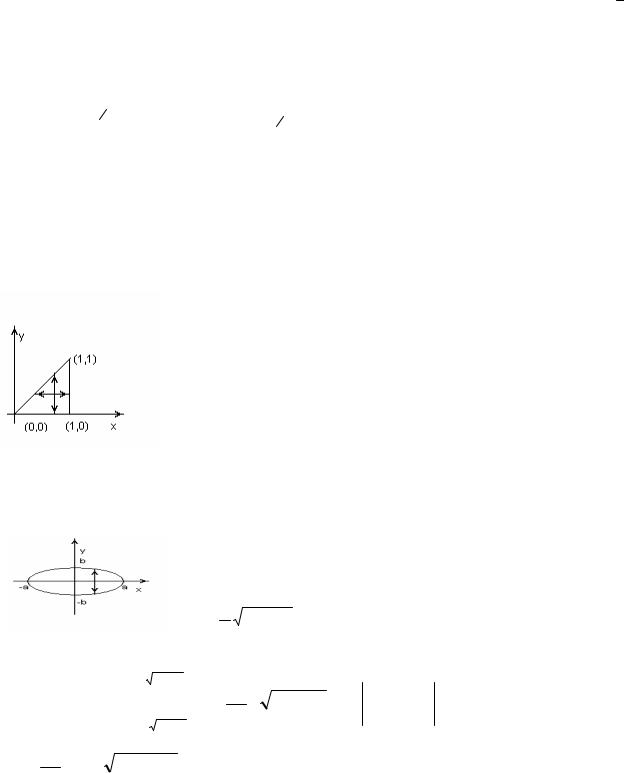
Пример 1: В двойном интеграле D расставить пределы интегрирования в том и другом порядке, если D – треугольник с вершинами О(0,0), А(1,0), В(1,1) .

∫∫ f (x, y)dxdy = ∫1		dx∫x	f (x, y)dy = ∫1	dy∫1	f (x, y)dx
Решение: D	o	0	0	y

Пример 2: Найти площадь, ограниченную эллипсом.

Решение:

y 2

= 1

Уравнение эллипса имеет вид: a2

; выразим y:

y = ± b

− x2

Тогда:

a 2 − x 2

замена

∫∫ dxdy

= 2∫a dx a

∫

dy = 4b ∫a

a 2

− x 2 dx =

−

− x

a 0

x = a sin t

1 / 2

/ 2

π / 2

4b a 2 ∫

1 − sin 2 t cos tdt

= 4ab ∫ cos 2 tdt = 2ab ∫ (1 + cos t )dt

π/ 2

=π ab + 2ab ∫ cos 2tdt = πab

	2			3− x
Пример 3. Записать выражение ∫1	2		dx ∫2
Пример 3. Записать выражение ∫1	dxx∫ f (x, y)dy + ∫3		dx ∫2		f (x, y)dy в виде одного двойного
0	0	1	0

интеграла, переменив порядок интегрирования.

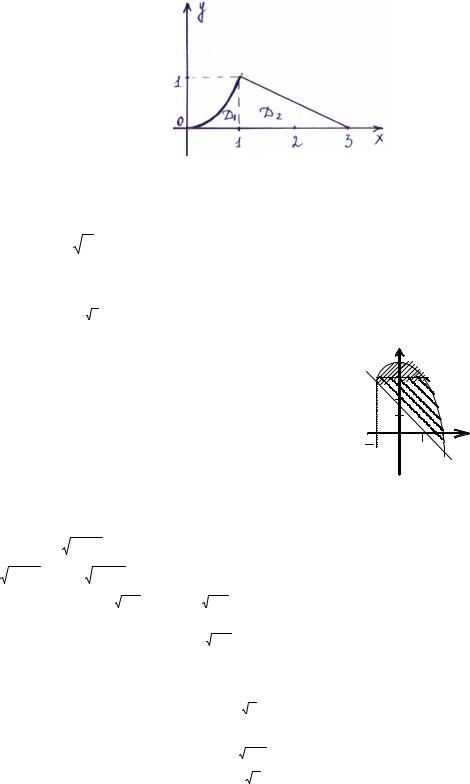
Решение. Напишем уравнения линий, ограничивающих области, на которые распространены данные двойные интегралы: D1

x = 0, y = 0	x = 1, y = 0
		3	− x . Тогда
	и D2
x = 1, y = x2	x = 3, y =
			2

область D= D1+ D2 есть простая.

Точку А(1;1) спроектируем на ось OY, получим область D, ограниченную снизу прямой y=0, сверху y=1, слева – линией x= y , справа - прямой x=3-2 y. Таким образом,

	x2		3− x	1	3−2 y
1	x2	3		1	3−2 y
∫dx ∫ f (x, y)dy + ∫dx ∫2				f (x, y)dy = ∫dy	∫ f (x, y)dx .
0	0	1	0	0	y

Пример 4. Изменить порядок интегрирования в двойном интеграле

2	4 − x 2
∫ dx	∫ f (x, y )dy.
− 1	2 − x

Решение. Определяем уравнения границы области, выписывая пределы изменения каждой из переменных:

− 1 ≤ x ≤ 2, 2 − x ≤ y ≤ 4 − x 2 .

4 y

1 2

Строим область, ограниченную линиями у = 2 − х, у = 4 − х2 Искомый интеграл будет выглядеть как сумма двух интегралов по областям:

• D1, где 0 ≤ y ≤ 3,			2 − y ≤ x ≤		4 − y ;
• D2, где 3 ≤ y ≤ 4,			−	4 − y ≤ x ≤ 4 − y .
2	4 − x 2	2		4 − x 2	3	4 − y	4	4 − y
∫ dx	∫ f (x, y )dy. = ∫ dx			∫ f (x, y )dy	= ∫ dy	∫ fdx	+ ∫ dy	∫ fdx .
− 1	2 − x	− 1		2 − x	0	2 − y	3	− 4 − y
Задачи:
								4		x
1. Изменить порядок интегрирования в интеграле ∫dx										∫dy
								0	−	4− x
								4	2+	x
2. Изменить порядок интегрирования в интеграле ∫dx									∫dy и найти площадь фигуры.
								0	x

3. Определить пределы интегрирования интеграла ∫∫ f (x, y)dxdy , если D ограничена

линиями y=x, y=2, x+y=6.

Двойной интеграл в полярной системе координат

Аудиторная и самостоятельная работа Двойной интеграл в полярных координатах

Если область D обладает симметрией вращения, то выгодно использовать замену

x = r cosϕ ,	y = r sinϕ ,				x2 + y 2 = r 2 cos2 ϕ + r 2 sin2 ϕ = r 2 , тогда
∫∫ f (x, y)dxdy =		ϕ	r		(r cosϕ ,r sinϕ )rdr
∫∫ f (x, y)dxdy =		∫2dϕ ∫2		f	(r cosϕ ,r sinϕ )rdr
D		ϕ1	r1

Пример 1. Вычислить площадь области D, ограниченной линией x2 + y 2 = R2 .

			R 2π	R	2π
	∫∫dxdy= ∫∫			ρdρdϕ = ∫ρdρ ∫dϕ =πR2
2	2	2	o 0	0	0
Решение x	+y	≤R

Пример 2. Переходя к полярным координатам, вычислить ∫∫(x2 + y 2 )dxdy ,

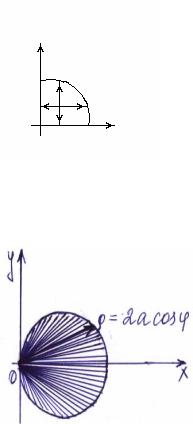
распространенный на область D, ограниченную окружностью x2+y2=2ax.

Решение.

Если x = ρ cosϕ

y = ρ sinϕ , то

f (ρ ,ϕ ) = ρ 2 cos2 ϕ + ρ 2 sin 2 ϕ = ρ 2

ρ 2

Уравнение окружности в полярных координатах имеет вид

= 2аρ cosϕ или ρ = 2аcosϕ . Область D ограничена лучами

ϕ = −

и ϕ = π

. При каждом фиксированном ϕ значение ρ

меняется от 0 до ρ = 2аcosϕ . На основании

формулы(*)

)dxdy =

2a cos ϕ

ρ 4

2a cos ϕ

+ cos 2ϕ ) dϕ

∫∫

+ y

∫

dϕ

∫

ρdρ

∫

dϕ

∫

16a

cos

ϕdϕ = a

∫

−

− π

−

3πa

= a

∫ (1

+ 2 cos ϕ

+ cos

2ϕ )dϕ = a

| + sin 2ϕ | +

sin 4ϕ

− π

−

∫∫ (x 2 + y 2 )dxdy

Ответ:

π a 4

Пример 3. Вычислить интеграл ∫∫ xydxdy			, где D – область, ограниченная эллипсом
		D
+	y2	= 1 и лежащая в первой четверти.
+	b2	= 1 и лежащая в первой четверти.
	b2

Решение.

Перейдем к полярным координатам ρ и ϕ по формулам x = aρ cosϕ и y = bρ sinϕ . Тогда уравнение эллипса примет

								вид			ρ 2 a 2 cos 2 ϕ									+	ρ 2 b 2 sin 2 ϕ	= 1 ρ 2 = 1, ρ	= 1,0 ≤ ϕ	≤	π
								вид												+	b 2	= 1 ρ 2 = 1, ρ	= 1,0 ≤ ϕ	≤	2
.														a 2							b 2				2
.
			π									π		2
			π									π
∫∫ xydxdy =			2	1								2	(ab)								1
∫∫ xydxdy =			∫ dϕ ∫ aρ cosϕbρ sinϕabρdρ							=		∫	(ab)		cosϕ sinϕdϕ ∫ ρ 3dρ =
D			0	0								0									0
	π					4				2			π				2		2
= (ab)2	2				ρ	4	1	= a2b2 sin		2		ϕ	2	1		a	2	b	2
	∫ sinϕd(sinϕ )				ρ		\|					ϕ	\|	1	=	a		b
	∫ sinϕd(sinϕ )						\|						\|		=
	0				4		0		2				0	4			8
Ответ:		a2b2
Ответ:			8
			8

Пример 4. Преобразовать к полярным координатам и расставить пределы у интеграла

		2Ry− y2
2∫Rdy ∫ f (x, y)dx .
	R	0
2

Решение.
Область D определяется следующими условиями:					R	≤ y ≤ 2R ; 0 ≤ x ≤ 2Ry − y 2 .
Область D определяется следующими условиями:				2		≤ y ≤ 2R ; 0 ≤ x ≤ 2Ry − y 2 .
				2
Перейдем к полярным координатам:	y =	R	; ρ sinϕ =	R		; ρ =	R	; y=2R; ρ sinϕ = 2R
Перейдем к полярным координатам:	y =	2	; ρ sinϕ =	2		; ρ =	2sinϕ	; y=2R; ρ sinϕ = 2R
		2		2			2sinϕ

ρ =	2R	; x = 2Ry − y 2 ; x2 + y 2 = 2Ry ; ρ 2 = 2R sinϕρ, ρ = 2R sinϕ .
	sinϕ

2sinϕ

Решаем совместно:

= 2R sin

2R sinϕ

2sinϕ

sin 2 ϕ =

; sinϕ =

; ϕ =

;

ϕ ;

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
26.07.2016399.9 Кб87высшая математика пособие для академических консультантов часть 3.pdf
#
26.07.2016277.65 Кб55высшая математика пособие для преподавателя часть 3.pdf
#
26.07.2016478.99 Кб75высшая математика пособие для студентов часть 3.pdf
#
26.07.2016835.31 Кб2554высшая математика руководство к решению задач часть 3.pdf
#
26.07.2016564.19 Кб139высшая математика Ряды-1.pdf
#
26.07.2016564.19 Кб94высшая математика Ряды.pdf
#
26.07.2016178.67 Кб17высшая математика структура дисциплины часть 3.pdf
#
26.07.2016113.73 Кб17высшая математика структура дисциплины часть 4.pdf
#
26.07.20161.43 Mб98высшая математика теоретический материал часть 3.pdf