Тройные интегралы в декартовой системе координат

Цель: научить вычислять тройные интегралы.

Вычисление тройного интеграла в декартовой системе координат ∫∫∫ f ( x, y,z )dxdydz ,

V

может быть осуществлено посредством ряда последовательных интегрирований.

Чтобы вычислить тройной интеграла по области V надо:

∫∫∫ f (x, y,z)dxdydz = ∫∫ dxdyz∫2 f (x, y,z)dz , где D –проекция области V на плоскость xoy, а

Рис 1

В случае когда D простая область, то тройной интеграл вычисляется по формуле:

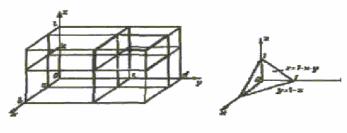
Если областью интегрирования служит внутренность параллелепипеда с гранями, параллельными координатным плоскостям (рис 2), то пределы интегрирования постоянны во всех трёх интегралах :

35

В этом случае интегрирование можно производить в любом порядке, пределы интегрирования будут при этом сохраняться.

Если же в общем случае менять порядок интегрирования (т.е., скажем, интегрировать сначала по направлению оси Оу, а затем по области плоскости Oxz), то это приведёт к изменению порядка интегрирования в тройном интеграле и к изменению пределов интегрирования по каждой переменной.

Пример 2. Вычислим тройной интеграл I = ∫∫∫(x + y + z)dxdydz,

Ω

где V – область, ограниченная координатными плоскостями x=0, y=0, z=0 и плоскостью x+у+ z=1 (пирамида, изображённая на рис.3).

Интегрирование по z совершается от z=0 до z = 1 - x - у. Поэтому, обозначая проекцию области V на плоскость Оху через D, получим

Расставим теперь пределы интегрирования по области D – треугольнику, уравнения сторон которого х = 0, у = 0, x+ у = 1:

36

Пример 3. Вычислить ∫∫∫ y cos(x + y)dxdydz , если V ограничена поверхностями

Пример 4. Вычислить интеграл

∫∫∫6x 2 ey + z dxdydz ,

T

где Т — область, ограниченная цилиндром х3 = у и плоскостями х = 0, у + z = 1, z = 0.

Решение. Построим данное тело (см. рис. 12.27) и представим данный интеграл по формуле

37

Задачи:

1. Вычислить ∫∫∫(2x + 3y − z)dxdydz , если область V- призма, ограниченная плоскостями

V

x = 0 , y = 0 , z = 0 , z = 3 , x + y = 2 .

Ответ: 11.

2. Вычислить ∫∫∫ xz 2 dxdydz , если область V- ограниченна плоскостями y = 0 , z = 0 ,

V

z = 3 ,. y = 2 , x = 2y − y 2

Ответ: 30.

Тройные интегралы в цилиндрических и сферических координатах

Цель: научить вычислять тройные интегралы в цилиндрических и сферических координатах

Аудиторная работа

Цилиндрическая система координат

Цилиндрическими координатами точки М являются числа r, ϕ, z, где 0 ≤ ϕ ≤ 2π ,

− ∞ < z < ∞ , 0 ≤ r ≤ ∞

Связь координат произвольной точки M пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по

x = r cosϕ

формулам: y = r sinϕ

z = z

Тогда тройной интеграл в цилиндрических координатах вычисляется по формуле:

∫∫∫ f ( x, y,z )dx dy dz = ∫∫∫ f ( r cosϕ ,r sinϕ ,z )r dr dϕ dz .

V V

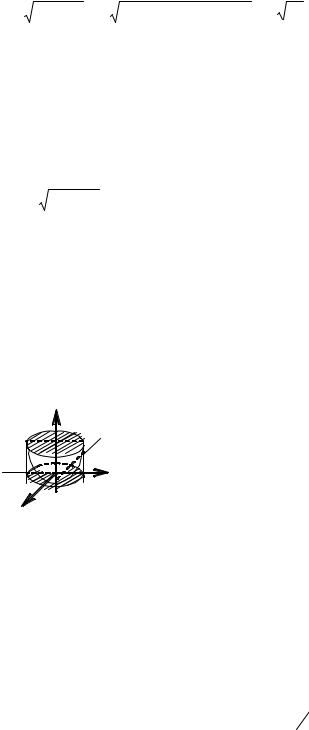
Пример 1. Вычислить ∫∫∫ z x2 + y 2 dxdydz , если V ограничена поверхностями z = 1,

v

x2 + y 2 = 2x , y ≥ 0 , z = 0 .

Область V проецируется на координатную плоскость в область D, ограниченную прямой у = 0 и дугой окружности

x2 + y 2 = 2x .

Поэтому перейдем к цилиндрическим координатам

38

где область Т ограничена параболоидом x2 + y2 = 2z и плоскостью z = 2

Каждая из поверхностей является соответственно геометрическим местом, первая – аппликат точек входа в область, вторая – аппликат точек выхода из области. Граница области Dxy – проекция линии

пересечения поверхностей – окружность:

Задачи:

1. Вычислить интеграл ∫∫∫ zdxdydz , преобразовав его к цилиндрическим координатам,

V

если область V, ограничена поверхностями x2 + y 2 + z 2 = 4 , z ≥ 1.

39

Самостоятельная работа

Сферическая система координат.

Сферическими координатами точки М являются числа r, ϕ, θ , где 0 ≤ ϕ ≤ 2π , 0 ≤ θ ≤ π , 0 ≤ r ≤ ∞

Связь координат произвольной точки М пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

x = r sinϕ cosθy = r sinϕ sinθz = r cosϕ

Тогда тройной интеграл в сферических координатах вычисляется по формуле:

∫∫∫ f ( x, y,z )dx dy dz = ∫∫∫ f ( r cosϕ sinθ ,r sinϕ sinθ ,r cosθ )r 2 sinθ dr dϕ dθ

V V