ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ТОЛЬЯТТИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «Высшая математика и математическое моделирование»
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
по высшей математике
часть III
Учебно-методическое пособие для студентов
Тольятти 2007
УДК 51(075.8) ББК 22.1я.73 Р 93
Научный редактор д.т.н., профессор П.Ф.Зибров
Р-93 Руководство к решению задач по высшей математике. Часть III. Учебнометодическое пособие для студентов. Сост.: Ахметжанова Г.В., Кошелева Н.Н., Павлова Е.С., - Тольятти: ТГУ, 2007.- стр. 70.
Учебно-методическое пособие соответствует курсу «Высшая математика». В данном пособии представлены модули: Дифференциальные уравнения, Кратные интегралы, Криволинейные и поверхностные интегралы. Рассмотрены типовые задачи и упражнения каждого модуля.
Утверждено научно-методическим советом факультета математики и информатики Тольяттинского государственного университета.
УДК 51(075.8) ББК 22.1я173
♥ Тольяттинский Государственный Университет
2
Содержание |
|
Модуль 9. Дифференциальные уравнения.................................................................................. |
4 |
Дифференциальные уравнения с разделяющими переменными......................................... |
4 |
Однородные дифференциальные уравнения. ........................................................................ |
4 |
Линейные неоднородные ДУ. Уравнения Бернулли. ........................................................... |
8 |
ДУ в полных дифференциалах.............................................................................................. |
13 |
ДУ второго порядка, допускающие понижение порядка................................................... |
17 |
Линейные неоднородные ДУ второго порядка с постоянными коэффициентами. ......... |
21 |
Линейные неоднородные уравнения II порядка с постоянными коэффициентами. |
|
Метод Лагранжа неопределенных коэффициентов. ........................................................... |
24 |
Модуль 10. Кратные интегралы................................................................................................. |
30 |
Понятие двойного интеграла. Вычисление двойного интеграла в декартовой системе |
|
координат ................................................................................................................................ |
30 |
Двойной интеграл в полярной системе координат ............................................................. |
33 |
Тройные интегралы в декартовой системе координат........................................................ |
35 |
Тройные интегралы в цилиндрических и сферических координатах............................... |
38 |
Приложение двойных и тройных интегралов...................................................................... |
41 |
Модуль 11. Криволинейные и поверхностные интегралы...................................................... |
46 |
Криволинейные интегралы первого рода. Приложение к решениям задач геометрии... |
46 |
Криволинейные интегралы второго рода. Формула Грина................................................ |
50 |
Основные понятия поверхностных интегралов 1 и 2 рода. Основные понятия теории |
|
поля.......................................................................................................................................... |
56 |
Список литературы..................................................................................................................... |
68 |
3
Тип |
уравнения |
разделяющимися |
переменными |
С |
|
Модуль 9. Дифференциальные уравнения
Дифференциальные уравнения с разделяющими переменными.
Однородные дифференциальные уравнения.
Цель: научить решать простейшие дифференциальные уравнения.
Аудиторная работа
Уравнением с разделяющимися переменными
Дифференциальные уравнения первого порядка y' = f (x, y) называется уравнением с разделяющимися переменными, если его правая часть есть произведение функций, одна из которых зависит от переменной x , другая – от y: y' = f1 ( x ) f2 ( y ) .
Уравнение, записанное в симметричной форме Р(x, y)dx + Q(x, y)dy = 0 является
уравнением с разделяющимися переменными, если множители P(x, y) и Q(x, y) представляют собой произведение функций, из которых одна зависит только от переменной x , другая – от переменной y :ϕ1(x) ϕ 2 ( y) dx + ψ 1(x) ψ 2 ( y) dy = 0 .
Разделить переменные – значит преобразовать уравнение так, чтобы каждая переменная содержалась только в том слагаемом, которое содержит её дифференциал.
Стандартная форма записи |
Особенности |
При дифференциалах –
ϕ1( x )ϕ 2 ( y )dx + +ϕ1( x )ϕ 2 ( y )dy = 0 произведения функций, зависящих одна
|
от x, другая – от y |
y' = f1( x ) f2 ( y ) |
Правая часть – произведение |
функций, зависящих одна |
|
|
от x, другая – от y |
Метод решения
|
ϕ1( x ) |
|
ϕ2 |
( y ) |
|
∫ |
ϕ ( x |
dx + |
ϕ |
( y ) dy = c |
|
|
1 |
|
2 |
|
|
∫ |
dy |
= ∫ f1( x )dx + c |
|||
f2( y ) |
|||||
|
|
|
|
||
Пример 1. Найти решение задачи Коши для уравнения ( x2 − 1 )y'−2xy = 0 , удовлетворяющее начальным условиям y(0)=1.
Решение:
10. Определим тип уравнения:
|
y' = |
|
|
2x |
y - уравнение с разделяющимися переменными, |
||||||||
x2 − 1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
где |
|
|
f1 (x) = |
|
|
2x |
|
, f 2 ( y) = y . |
|||||
|
|
x 2 − 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
20. Разделим переменные: |
|||||||||||||
|
dy |
|
= |
|
2x |
|
|
|
y; |
|
|||
|
dx |
|
x2 − |
1 |
|
||||||||
|
|
|
|
|
|
|
|||||||
|
dy |
|
= |
|
2x |
|
|
|
dx. |
|
|||
|
y |
|
x2 − |
1 |
|
||||||||
|
|
|
|
|
|
|
|||||||
30. Проинтегрируем обе части равенства:
4
∫ |
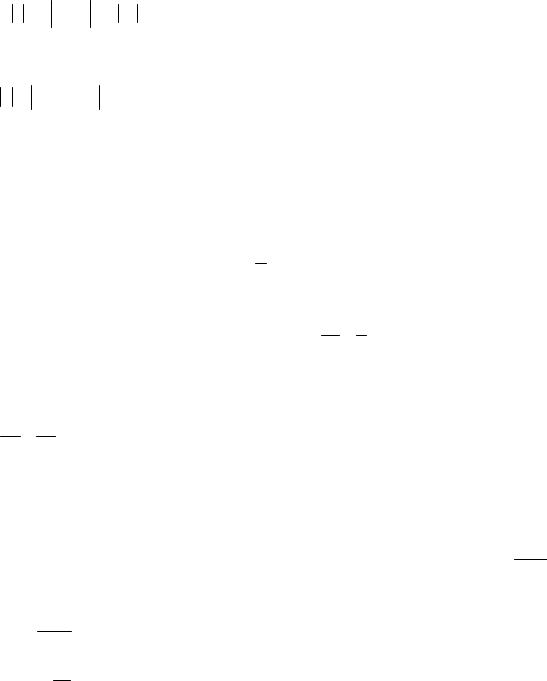
dy |
= ∫ |
2x |
dx, . |
y |
|
|||
|
|
x2 − 1 |
||
ln y = ln x2 − 1 + ln C1
Для удобства преобразований постоянная выбрана в логарифмической форме. 40. Упростим результат интегрирования:
y = c1 ( x 2 −1) ,
y = ±c ( x 2 −1), г ± c = c,то |
|
1 |
1 |
y = c( x 2 |
−1). |
50. Подставим начальные условия. При x=0, y=1 получаем с= − 1 . 60. Запишем ответ: y = 1 − x2 .
Пример 2. Решить уравнение y' = xy .
Решение:
Это уравнение с разделяющими переменными dydx = xy , откуда ydy = xdx.
Проинтегрируем обе части равенства
∫ ydy = ∫ xdx ,
y22 = x22 + С1 .
Преобразуем полученное выражение
y 2 − x2 = С2 ,
x2 − y 2 = С.
Пример 3. Найти общее решение дифференциального уравнения: yy′ = − 2x cos y
Решение:
yy′ = − 2x cos y
y cos y dydx = −2x y cos ydy = −2xdx
∫ y cos ydy = −2∫ xdx
Интеграл, стоящий в левой части, берется по частям
∫ y cos ydy = u = y; dv = cos ydy; = y sin y − ∫sin ydy = y sin y + cos y |
|
du = dy; v = sin y |
|
5
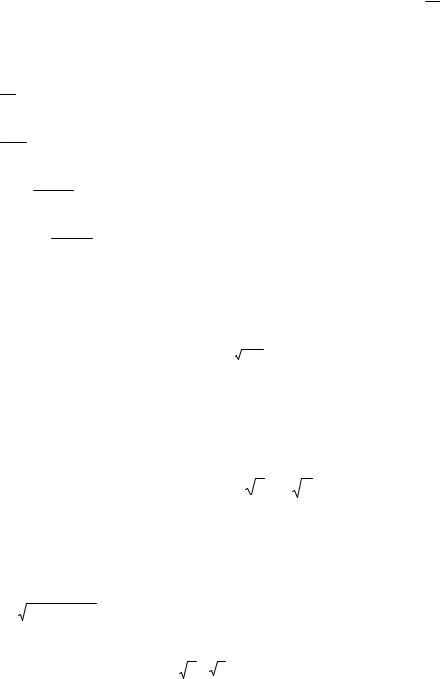
y sin y + cos y = − x2 + C
y sin y + cos y + x2 + C = 0 .
Пример 4. Найти решение дифференциального уравнения yy′ = ln y при условии
у(2) = 1.
Решение: yy′ = ln y
ydxdy = ln y
dx = ln ydy y
∫dx = ∫ ln ydyy
x+ C = ∫ln yd(ln y)
x + C = |
ln2 y |
|
при у(2) = 1 получаем |
2 + C = |
ln2 1 |
|
; 2 + C = 0; C = −2; |
||||||
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|||
Итого: 2(x − 2) = ln2 y; или y = e± 2 x−4 - частное решение; |
|||||||||||||
|
Решить дифференциальные уравнения: |
|
|||||||||||
а) |
y 2 y' = 1 − 2x |
|
е) y' = y 2 cos x ; |
|
|
|
|
|
|||||
б) |
xy'+ y = y 2 ; |
|
|
ж) ( x + 2x3 )dx + ( y + 2 y 3 )dy = 0 ; |
|||||||||
в) y' = 10 x+ y ; |
|
|
з) |
x y'= y ; |
|
||||||||
г) y'= y ln y ; |
|
|
и) yp'= − p + p2 ; |
||||||||||
д) |
sin x sin y dx + cos x cos y dy = 0 ; к) a( xy'+2 y ) = 2xyy' . |
|
|||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|||
|
а) |
|
е) |
y( С − sin x ) = 1 |
|
||||||||
y = 3 С + 3x − 3x 2 |
|
|
|
|
|
|
|
|
|
|
|||
|
б) Сxy = y − 1 |
|
ж) x2 + y2 + x4 + y4 = С2 |
|
|||||||||
|
в) |
|
з) |
y − x = C |
|
|
|
|
|
||||
y = − lg( С − 10 x ) |
|
|
|
|
|
|
|
|
|
|
|||
|
г) ln y = Сe x |
|
и) py = C( p − 1 ) |
|
|||||||||
|
д) sin y = С cos x |
к) |
|
2 y |
|
|
|
|
|
|
|||
|
x2 y = Ce a |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
Самостоятельная работа
Однородные дифференциальные уравнения I порядка и уравнения приводимые к однородным
6
Дифференциальное уравнение Ι порядка y' = f ( x, y ) называется однородным дифференциальным уравнением, если его правая часть – однородная функция нулевого
y |
|
x |
|
y |
||||
|
|
|
|
|
|
y' = f |
|
|
|
|
|
||||||
|
|
|
|
x . |
||||
порядка, т.е. функция отношения |
x |
(или |
y ), или |
|||||
Уравнение, записанное в симметричной форме P( x, y )dx + Q( x, y )dy = 0 , является
однородным уравнением, если функции P( x, y ) и Q( x, y ) порядка.
Тип уравнения |
Стандартная форма записи |
|
|
|
|
|
|
Особенности |
Метод решения |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y |
|
|
|
|
|
|
|
Правая часть – однородная |
|
y |
|||||||||
|
y' = f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= u( x ) |
||||||
Однородное |
x |
|
|
|
|
|
|
|
функция нулевого порядка |
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
функции одинакового порядка |
|
y = u x, y' = u' x + u |
||||||||||
|
P( x, y ) dx + +Q( x, y ) dy = 0 |
|
|
|
|
|
|
|
P( x, y ),Q( x, y ) - однородные |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = |
|
y |
y |
|
|
|
|
||||
|
Пример 5. Решить уравнение |
|
|
ln |
|
+ 1 . |
|
|
|
|||||||||||||
|
|
|
x |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
|
Решение: Введем вспомогательную функцию u. |
|
|
|
||||||||||||||||||
|
u = |
y |
; y = ux; y′ = u′x + u . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Подставляем в исходное уравнение: |
|
|
|
|
|
|
|
|
|
||||||||||||
|
u′x + u = u(lnu + 1); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
u′x + u = u ln u + u; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
u′x = u ln u; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
du |
= |
dx |
; |
|
|
|
|
|
|
|
|
|
|||
|
Разделяем переменные: u ln u |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
∫ |
du |
|
= |
∫ |
dx |
; |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
u ln u |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
ln ln u = ln x + C;
Интегрируя, получаем: ln u = Cx; u = eCx ;
Переходя от вспомогательной функции обратно к функции у, получаем общее решение: y = xeCx .
7