Расчет на прочность стержневых систем

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

Сопротивление материалов

Файл:

0,58 cos 20

cos 25 5,047 cos 25 4,574 кН;

sin 25 5,047 sin 25 2,133 кН;

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

1.26 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

9 Определяют коэффициенты запаса прочности в предполагаемых опасных сечениях вала и сравнивают их с заданными значениями.

Если вычисленный коэффициент запаса прочности не соответствует заданному, то следует изменить диаметр вала и повторить расчёты.

Примечания:

1 Концентраторами напряжений являются: под шестерней – шпоночный паз, под опорой – напрессованное внутреннее кольцо подшипника (давление напрессовки 20 МПа).

2 В расчётах учитывают, что поверхность вала шлифованная.

4.3 Пример выполнения работы

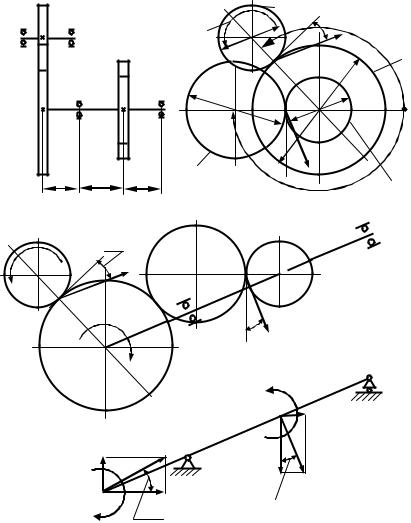
Подобрать диаметр вала АВ зубчатой передачи, изображённой на рис. 18, при следующих данных: N = 73кВт, n = 1050 об/мин, D 1 = 28 см,

D2 = 58 см, D3 = 26 см, D4 = 42 см, l1 = 18 см, l2 = 20 см, l3 = 20 см, β = 135°, γ = 180°, α = 20°, n необх = 1,4...1,7, поверхность вала шлифован-

ная, материал вала – сталь 45.

Используя исходные данные, изобразим в масштабе схему зубчатой передачи (рис. 20, а). Покажем усилия F12 и F43, действующие на зубчатые колеса 2 и 3 вала АВ.

Изобразим отдельно вал АВ с зубчатыми колесами 2 и 3 и действующими на них силами (рис. 20, б).

Изобразим расчётную схему вала (рис. 20, в), перенося усилия F12 и F43 на ось вала, раскладывая их на вертикальные и горизонтальные составляющие и добавляя моменты m2, m3.

Определим по мощности и числу оборотов моменты, действующие на вал:

m 2 m3		9,55		N	;
m 2 m3		9,55		n 2	;
				n 2
где n 2 n1	D1		1050			0,28		507,0 об/мин ,

	D 2					0,58
	D 2					0,58
тогда m 2 m3			9,55		N		9,55		73	1,375 кН м.
тогда m 2 m3			9,55				9,55			1,375 кН м.
					n 2				507

а)			n1
			n1
E	C	В	D4
А	C
А
			4
0,18	0,20 м 0,20
б)
	20º
	F12
n 1			E
			E

n 2

	E
в	F2
F 2
в)
А	F г2
m 2	25º

β = 135º

2 0 º F12

F43

2 0 º

γ = 180º

F43

20º

m 3
C		F	г
		F	3
F в		F
3	3
	20º

Рисунок 20 – Расчётная схема зубчатой передачи

Определим усилия, действующие на вал, и их проекции в горизонтальной и вертикальной плоскостях:

F 3		2 m 3			2 1,375	11,26 кН ;
		D 3	cos		0,26 cos 20

F 3г	F3 sin 20 11,26 sin 20 3,850 кН;
F 3в F2			cos 20	11,26 cos 20 10,58 кН.

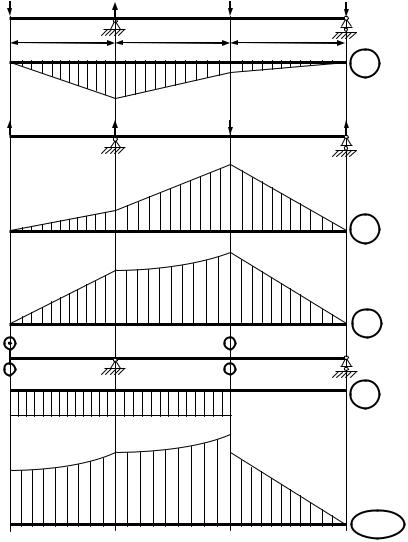
Строим эпюры изгибающих моментов М г, М в от сил, действующих в горизонтальной и вертикальной плоскостях, а также эпюры суммарного изгибающего момента М и, крутящего момента М к и эквивалентного момента M экв IV (рис. 21).

Определим диаметр вала в первом приближении из условия статической прочности при изгибе с кручением, используя заниженное допускаемое напряжение:

				M наиб					1
наибэкв				экв IV					1		,
наибэкв											,
IV				W x					n cp
				W x					n cp
где W x			d 3I		,	n cp		1,4 1,7				1,55,	для стали 45: в = 600-750 МПа;
где W x		32			,	n cp						1,55,	для стали 45: в = 600-750 МПа;
		32							2
т = 320 МПа; -1 = 250-340 МПа.
Тогда

	32 M наибэкв IV					n cp
d 3	32 M наибэкв IV					n cp	3			32 1,727 10 3			1,55	44,78 мм.
d 3				1			3				250 10 6			44,78 мм.
				1							250 10 6

Принимаем ближайшее стандартное значение d = 45 мм.

W x W y	d I3	4,5 3	8,946 см 3 ,	W р 2 W х	2 8,946 18,89 см 3 .
	32	32

Фактически напряжения во вращающемся вале циклически изменяются.

Определим коэффициенты запаса вала по текучести и усталости в предполагаемых опасных сечениях.

	4,573 кН	8,556 кН			3,850 кН		0,133 кН
А	0,18 м	Е	0,20 м	С		0,20 м	В
	0,18 м		0,20 м			0,20 м
							Mг	,
					0,0266		кНм
							кНм
		0,8231
2,132 кН		2,199 кН			10,58 кН		6,249 кН
				1,25
	0,3838
							M в	,
					1,25		кНм
							кНм
	0,9082
							Mи	,
1,375 кНм				x	1,375 кНм		кНм
							кНм
x				x
				1 , 3 7			Mк	,
				1 , 3 7
				1,727			кНм
				1,727
	1,498				1,25
	1,191
							M экв IV		,
	Рисунок 21 – Эпюры внутренних сил						кНм

Сечение Е (концентратор – напрессованное внутреннее кольцо подшипника). Определим напряжения в опасной точке сечения (точке, расположенной на поверхности вала), учитывая, что нормальные напряжения изменяются по симметричному закону, а касательные напряжения постоянны:


		M E					0,9084 10			3
max min			u								101,5 М Па,
		W x					8,946 10 6
	M E					1,375 10		3
		к
max min									76,86 М Па.
	W р				18,89 10 6
Тогда а = 101,5				МПа, m = 0, а = 0, m = 76,86 МПа. Из справочных

данных [2] найдём значения остальных величин, входящих в формулы для коэффициентов запаса:

передаётся сила; ξ΄ = 1,339 при в = 750 МПа; ξ΄΄ = 0,957 при р = 20

МПа; тогда;

k d

		k


		k
			d
			d

3 1,339 0,957 3,84;

k F = 0,94 при в = 750 МПа, шлифовка; k V = 0 – упрочняющей обработки нет. Теперь находим коэффициенты запаса:

n т

320

1,91;

m2 ax 3 m2 ax

101,5 2 3 76,86 2

250

0,603;

3,84

a m

101,5

k d k F k v

0,94 1

150

39,03;

0,05 76,86

k d k F k v

n R

0,603 39,03

0,603.

n 2

0,603 2 39,03 2

Подсчитаем коэффициенты запаса в сечении С (концентратор – шпоночный паз).

Из сборника справочных данных [2]: Wu = 7,80 см3; WK = 16,74 см3 для вала со шпоночным пазом, при d = 45 мм.


		M C			1,2503 10					3
			u		1,2503 10
max min											160,3 М Па,
max min		W u				7,8 10 6					160,3 М Па,
	M C				1,375 10		3
max min		к			1,375 10				82,14 М Па. .
max min				16,74 10				6	82,14 М Па. .
	W к			16,74 10				6

Тогда а = 160,3 МПа, m = 0, а = 0, m = 82,14 МПа. Из справочных данных [2] найдем значения остальных величин, входящих в формулы для коэффициентов запаса: σ = 0,1 и = 0,05; kF = 0,94; kV = 1, kσ = 1,75 и kτ = 1,75 при в = 750 МПа (шпоночный паз); kd = 0,803 прив = 500 МПа, kd = 0,693 при в = 1400 МПа и d = 45 мм. Интерполируем для в = 750 МПа:

	k d 0,693								0,803 0,693				(1400 750 ) 0,77.
	k d 0,693												(1400 750 ) 0,77.
									1400 500
	Находим коэффициенты запаса:
n т					т							320						1,49;


				m2 ax 3 m2 ax								160,3 2 3 82,14 2
n							1										250					0,645;
n				k										1,75								0,645;
				k				a				m		1,75					101,5		0


			k d k F k v											0,77 0,94 1
n						1								150						36,52;
n				k										0,05			82,14			36,52;
				k								0		0,05			82,14
							a			m
		k d k F k v					a			m
		k d k F k v
n R				n	n						0,645 36,52				52	0,645.
n R															52	0,645.
				n 2	n 2					0,645 2 36,52 2

Коэффициент запаса вала, равный наименьшему из четырёх найденных значений, п = 0,603, ниже заданного, поэтому диаметр вала необходимо увеличить и повторить расчёт для наиболее опасного сечения Е. Для второго приближения диаметр вала можно ориентировочно подсчитать по формуле

d II d I 3	n cp	45		1,55	61,6 мм .
d II d I 3	n I	45	0,603		61,6 мм .
			3

Принимаем ближайшее стандартное значение d = 62 мм.

W x W y	d II3	6,2 3	23,40 см 3 ,	W р 2 W х	2 23,4 46,8см 3 .
	32	32

Определяем коэффициент запаса в наиболее опасном сечении Е:


		M E			0,9084 10			3
max min			u						38,82 М Па,
		W x			23,4 10 6
	M E			1,375 10		3
max min		к					29,38 М Па.
	W р			46,8 10 6

Тогда а = 38,82 МПа, m = 0, а = 0, m = 29,38 МПа. Из справочных данных [2] найдём значения остальных величин, входящих в формулы

для коэффициентов запаса: σ = 0,1 и = 0,05; k F = 0,94; k v = 1;
	k			= 3,182 при d = 62 мм, передаётся сила; ξ΄ = 1,339; ξ΄΄ = 0,957,


	k
		d	0

	k		k
тогда						3,182 1,339 0,957 4,08; .
тогда						3,182 1,339 0,957 4,08; .
	k		k
		d		d	0

Коэффициенты запаса:

n т				т					320					5,00;


			m2 ax 3 m2 ax					38,82 2		3 29,38 2
n						1						250				1,48;
n			k							4,08						1,48;
			k			a m				4,08			38,83		0
						a m							38,83		0
		k d k F k v									0,94 1
n					1					150					38 102;
n			k								0,05 29,14				38 102;
			k			a			0		0,05 29,14
	k d k F k v					a			m
	k d k F k v
n R			n	n				1,48 102			52 1,48.

			n 2	n 2			1,48 2 102 2
			n 2	n 2			1,48 2 102 2

Подобранный диаметр d = 62 мм обеспечивает коэффициент запаса вала n = 1,48, что находится в требуемом интервале 1,4…1,7.

4.4 Контрольные вопросы

1 Какой вид сопротивления испытывает вал зубчатой передачи?

2 Как записывается условие статической прочности вала круглого поперечного сечения при изгибе с кручением?

3 Почему вал зубчатой передачи испытывает циклически изменяющиеся напряжения?

4Где располагаются опасные сечения вала?

5Что такое концентрация напряжений и как она влияет на прочность?

6Как влияют размеры вала на сопротивление усталости?

7Как влияет состояние поверхности вала на сопротивление устало-

сти?

8Как записывается условие прочности при циклически изменяющихся напряжениях?

9Как определяют коэффициент запаса вала по усталости при изгибе

скручением?

10Как определяют коэффициент запаса вала по текучести при изгибе с кручением?

5. РАСЧЁТ БАЛКИ ПРИ КОЛЕБАНИЯХ

5.1 Задание

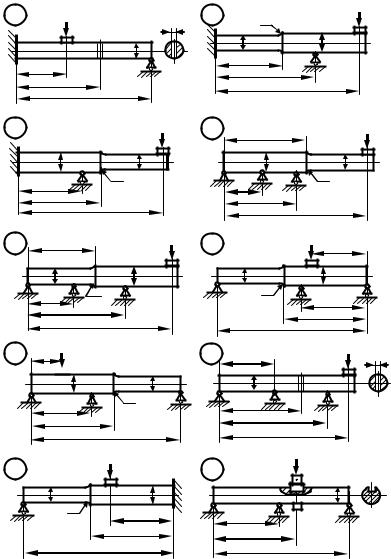
Заданы схема статически неопределимой балки круглого поперечного сечения (рис. 22), загруженной постоянной силой G (сила веса груза)

игармонически изменяющейся силой Fa sin t, размеры, частота изменения переменной силы, материал балки и необходимый коэффициент запаса (табл. 5).

Требуется определить размеры поперечного сечения балки.

Впояснительной записке следует представить схему балки, выполненную в масштабе, эпюры изгибающих моментов от заданных и единичных сил, диаграмму предельных амплитуд цикла напряжений балки

ивсе необходимые расчёты.

5.2Порядок выполнения работы

1По данным табл. 5 изображают в масштабе схему балки, соответствующей заданному шифру.

2Раскрывают статическую неопределимость балки методом сил, считая, что балка нагружена силой Q = F 0 + G.

3Строят эпюры изгибающих моментов от силы Q.

4По значениям изгибающих моментов на персональном компьютере вычисляют перемещения балки, строят изогнутую ось и оценивают погрешность раскрытия статической неопределимости.

5Назначают предварительные (первая попытка) размеры поперечного сечения балки из условия статической прочности при изгибе силой

	M наиб	1
Q: наиб	Q		,
	W x
		n cp

где пср – среднее значение заданного коэффициента запаса.

6 Определяют частоту собственных колебаний балки подобранных размеров и убеждаются, что её можно считать системой с одной степенью свободы.

7 Вычисляют коэффициент усиления колебаний, приняв = 0,03.

	F0·sin t	d 1	6	r	F0·sin t
	G			d	D	G
	D			d	D
				b	a
a					a
a					l
	l				l
	l
	F0·sin t		7	a	F0	sin t
				a
		G
	d	G		D		G
	d			D		d
	r			c	r
a				c
a	l			b	l
	l				l

3	a	F0·sin t
		F0·sin t
		G
d		D
c		r
c		b
		b

4 cc F0 sin t G

D	d
b a	r
b a
	l

5	F0·sin t	G
		G
d		D
	r	b
		b
		a
	l

8		F0	sin t		c
				G
		r			a b
			l		a b
			l
9	c			F0	sin t	d 1
	D					G
	D
	b		а
			а
				l
10	F0	sin t		G
				G
					D
	b
		a
			l

Рис. 22. Схемы балок (см. также с. 52 и 53)

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете Сопротивление материалов

#
16.03.2015772.06 Кб60В.С Вакулюк, А.В. Чирков, В.К. Шадрин СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ.pdf
#
16.03.2015648.95 Кб29изгиб и устойчивость.PDF
#
16.03.20152.42 Mб49Методика решения нестандартных задач.pdf
#
29.03.2016209.3 Кб43ПОЯСНИТЕЛЬНАЯ ЗАПИСКА «Расчет статически определимых балок» Вариант № 11.docx
#
16.03.2015429.72 Кб24Припадчев гр.1207 Сопромат(3 семестр, РГР1).pdf
#
29.03.20161.26 Mб37Расчет на прочность стержневых систем.pdf
#
16.03.2015700.43 Кб33Расчёт на прочность.pdf
#
29.03.2016516.82 Кб33Расчетно-проектировочные работы по сопротивлению материалов.pdf
#
16.03.2015613.54 Кб45СБОРНИК РАСЧЕТНО-ПРОЕКТИРОВОЧНЫХ РАБОТ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ.pdf
#
29.03.2016152.26 Кб33СОПРОМАТ 2-ая 561.docx
#
16.03.2015342.37 Кб37СОПРОМАТ 1 РГР Вариант 548.docx